 |
Пример применения 1-ой (основной) теоремы двойственности
|
|
|
|
Двойственные задачи линейного программирования
Каждой задаче ЛП соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности оказалась полезной для проведения исследования ЗЛП.
Экономическая интерпретация двойственной задачи к задаче об использовании ресурсов
Определить, сколько надо выпускать продукции первого и второго вида, чтобы общая прибыль была максимальна. Прибыль от выпуска единицы П1 – 7 рублей, П2 – 5 рублей. Имеется 4 вида ресурсов, которые идут на изготовление этой продукции (запасы ресурсов – 19, 13, 15 и 18 единиц соответственно).
Пусть математическая формулировка задачи об использовании ресурсов такова:
 (1)
(1)
|
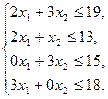 (2),
(2),
 (3).
(3).
Предположим, что некоторая организация желает приобрести сырье, которым располагает предприятие. По какой цене эта организация стала бы покупать указанное сырье, обозначим, соответственно, через  , цену единицы сырья вида
, цену единицы сырья вида 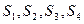 .
.
Выручка от продажи всего сырья, расходуемого на единицу продукции вида  по ценам
по ценам  , составит
, составит  . Предприятию выгодно продавать сырье, если
. Предприятию выгодно продавать сырье, если
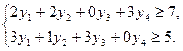
С другой стороны общая стоимость всех запасов сырья, приобретаемого составит 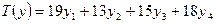 (4). Ясно, что покупающая организация стремится приобрести сырье по возможности дешевле, то есть минимизирует форму (4). Таким образом
(4). Ясно, что покупающая организация стремится приобрести сырье по возможности дешевле, то есть минимизирует форму (4). Таким образом
 (4)
(4)
при ограничениях
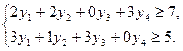 (5),
(5),
 (6).
(6).
Цены Y1, Y2, …, Ym в экономической литературе получили названия: учетные, неявные, теневые. Смысл в том, что это условные, «ненастоящие» цены. Их часто называют оценками ресурсов.
Две задачи линейного программирования (1) - (3), (4) - (6), связанные подобного рода особенностями называются взаимно двойственными или сопряженными.
|
|
|
Прямая и двойственная задачи (слайд 3)
| Исходная задача | Двойственная задача |
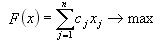 при ограничениях
при ограничениях
| 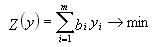 при ограничениях
при ограничениях
|
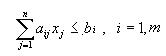

| 

|
| Составить такой план выпуска продукции Х = (Х1, Х2, …, Хn), при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющиеся запасы | Найти такой набор цен (оценок) ресурсов У = (У1, У2, …, Уm), при котором общие затраты на ресурсы будут минимальные при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции |
Общие правила составления двойственных задач:
1) В одной задаче ищут максимум ЛФ, в другой – минимум.
2) Свободные члены ограничений одной из задач являются коэффициентами при соответствующих переменных в целевой функции другой задачи. При этом максимум меняется на минимум и наоборот.
3) Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида «<=», а в задаче минимизации все неравенства вида «>=».
4) Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг другу.
5) Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6) Условия неотрицательности переменных имеются в обеих задачах
Первая (основная) теорема двойственности
Теорема: Если однаиз сопряженныхзадач имеет оптимальное решение 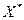 , то и вторая имеет оптимальное решение
, то и вторая имеет оптимальное решение 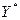 , при этом
, при этом
Fmax = Zmin или F(X*) = Z(Y*).
Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы.
Пример применения 1-ой (основной) теоремы двойственности
Задача. Дана задача (рассматривали в лекции по симплекс-методу):
F = 2x1 + 3х2 à max при ограничениях:
 х1 + 3х2 <= 18
х1 + 3х2 <= 18
2х1 + х2 <= 16
х2 <= 5
3x1 <= 21
х1, х2 >= 0
|
|
|
и двойственная к ней:
Z =18y1 + 16y2 +5y3 + 21y4 à min при ограничениях:
 y1 + 2y2 + 3y4 >= 2
y1 + 2y2 + 3y4 >= 2
3y1 + y2 + y3 >= 3
y1, y2, y3, y4 >= 0
Прямая задача была решена в лекции о симплекс-методе и был получен ответ F max = 24. если решить симплекс-методом двойственную задачу, то будет получен ответ, что Z min = 24. Т.е. заключение первой части теоремы двойственности верно.
|
|
|


