Вероятность попадания в область произвольной формы

При стрельбе ударными снарядами вычисление вероятности попадания в цель сводится к вычислению вероятности попадания случайной точки 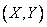в некоторую область 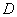. Пусть случайная точка 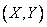подчинена нормальному закону в каноническом виде. Вероятность попадания точки 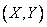в область 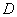выражается интегралом

. (9.5.1)

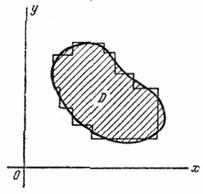
Рис. 9.5.1

В отдельных частных случаях (например, когда область 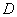есть прямоугольник со сторонами, параллельными главным осям рассеивания, или эллипс рассеивания, а также в некоторых других, имеющих меньшее практическое значение) интеграл (9.5.1) может быть выражен через известные функции; в общем же случае этот интеграл через известные функции не выражается. На практике для вычисления вероятности попадания в область произвольной формы применяются следующие приближенные способы.

1. Область 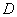приближенно заменяется областью, составленной из прямоугольников, стороны которых параллельны главным осям рассеивания (рис.9.5.1). Вероятность попадания в каждый из таких прямоугольников вычисляется по формуле (9.3.3). Этот способ можно рекомендовать тогда, когда число прямоугольников, на которые приближенно разбивается цель , не слишком велико.

2. Вся плоскость с помощью некоторой системы линий (прямых или кривых) заранее разбивается на ряд ячеек, вероятности попадания в которые могут быть выражены точно через известные функции, и вычисляетсявероятность попадания в каждую ячейку. Такая система линий с соответствующими ей вероятностями попадания в ячейки называется сеткой рассеивания. Работа с сеткой заключается в том, что изображение сетки накладывается на изображение цели, после чего производится суммирование вероятностей попадания в ячейки, накрытые целью; если цель накрывает часть ячейки, то берется часть вероятности попадания в ячейку, пропорциональная накрытой площади.

Сетку рассеивания можно применять двояким образом: а) строить цель в масштабе сетки, б) строить сетку в масштабе цели.

Если цель имеет сложные очертания и, особенно, если она сравнительно невелика, бывает обычно удобнее построить на изображении цели в том же масштабе ту часть сетки, которая занята целью. Если же цель имеет сравнительно простые очертания и довольно велика (занимает значительную часть полного эллипса рассеивания) обычно удобнее построить цель в масштабе сетки. Так как стандартная сетка строится для кругового рассеивания, а на практике рассеивание в общем случае круговым не является, при построении цели в масштабе сетки приходится в общем случае пользоваться двумя разными масштабами по осям и . При этом способе удобно иметь в распоряжении сетку рассеивания, выполненную на прозрачной бумаге, и накладывать ее на перестроенное изображение цели. Прямолинейная сетка рассеивания для одного координатного угла дана на рис. 9.5.2. Сторона ячейки равна .

Рис. 9.5.2

В ячейках проставлены вероятности попадания в них, выраженные в сороковых долях процента.

1. В случае, когда размеры области 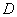невелики по сравнению со средними квадратическими отклонениями (не превышают с.к.о. в направлении соответствующих осей), вероятность попадания в эту область может быть приближенно вычислена по формуле, не содержащей операции интегрирования.

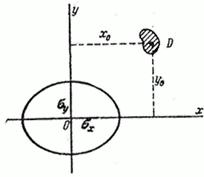
Рис. 9.5.3

Рассмотрим на плоскости малую цель 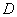произвольной формы (рис. 9.5.3). Допустим, что размеры этой цели невелики по сравнению с вероятными отклонениями . По общей формуле (8.3.3) имеем:

. (9.5.2)

где - плотность распределения системы 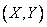. Применим к интегралу (9.5.2) теорему о среднем значении:

,

где — некоторая точка внутри области — площадь области .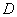

В случае, когда система 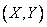подчинена нормальному закону в каноническом виде, имеем:

. (9.5.3)

При сравнительно малых размерах области 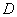плотность распределения в пределах этой области изменяется мало и практически может быть принята постоянной. Тогда в качестве точки можно выбрать любую точку в пределах области 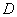(например, приблизительный центр цели).

Формулы типа (9.5.3) широко применяются на практике. Для областей, наибольшие размеры которых не превышают среднего квадратического отклонения в соответствующем направлении, они дают вполне приемлемые по точности результаты. В отдельных случаях их применяют и для более крупных областей (порядка одного с.к.о.). При условии внесения некоторых поправок (а именно, замены величин несколько увеличенными значениями) область применимости этой формулы может быть расширена на области размером порядка двух с.к.о.