 |
Выдвижение гипотезы о законе распределения генеральной совокупности
|
|
|
|
По виду гистограммы можно предположить, что случайная величина имеет равномерное распределение.
Выдвигаем гипотезу о равномерном законе распределения генеральной совокупности.
Оценка числовых характеристик и параметров закона распределения.
Выборочное среднее 
– несмещенная и состоятельная оценка математического ожидания.
Исправленная выборочная дисперсия 
– несмещенная и состоятельная оценка дисперсии.
Выдвинута гипотеза о распределении генеральной совокупности Х по равномерному закону с плотностью 
Найдем 
- оценки параметров a и b теоретического закона - крайних значений выборки, которые находятся из системы 
.
Имеем 
Следовательно, 
Заменяя a, b оценками 
, получаем теоретический закон распределения 
Нахождение доверительного интервала для математического ожидания
Полагая, что генеральная совокупность Х имеет нормальное распределение, построим доверительный интервал для математического ожидания при неизвестном среднем квадратическом отклонении.
В курсе математической статистики доказывается, что случайная величина Т в случае выборки из нормальной совокупности, имеет распределение Стьюдента c (n –1)-й степенью свободы, не зависящее от параметров генеральной совокупности. Доверительный интервал с выбранной надежностью 
, покрывающий математическое ожидание, будет иметь вид 
. Для нахождения точности оценки 
значение 
определяется по таблице распределения Стьюдента по заданной надежности и по числу степеней свободы k = (n – 1).
Построим 95% доверительный интервал для оценки математического ожидания. Тогда имеем = 0,95, число степеней свободы k = 60-1=59, уровень значимости α=1– =0,05. По таблице распределения Стъюдента находим =2. 
= 
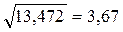. Точность оценки 
.
|
|
|
Получаем доверительный интервал для оценки математического ожидания нормально распределенной генеральной совокупности:
Окончательно имеем (12,611; 14,523).
Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона.
В качестве меры расхождения между статистическим и гипотетическим (теоретическим) распределениями возьмем критерий Пирсона К = χ2.
Мера расхождения в этом критерии определяется равенством: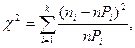 
где n – объем выборки (у нас n = 60); ni – эмпирические частоты (число элементов в i -ом интервале); K – число интервалов (у нас K = 7); Pi – теоретические вероятности попадания значений случайной величины в i -ый интервал, 
– теоретические частоты.
В рассматриваемом эмпирическом распределении имеются частоты, меньшие 5. При использовании критерия Пирсона такие интервалы целесообразно объединять с соседними. После объединения интервалов с низкой степенью частоты получим вспомогательную таблицу 5.
Таблица 5
| 
| 
| 
| 
| 
| 
| 
|
|
Находим теоретические вероятности Pi по формуле: 
.
.
….
Дальнейшие вычисления, необходимые для определения расчетного значения выборочной статистики 
, проведем в таблице 6.
Таблица 6
|
|
|
|
|
|
|
|
|
|
| |||||||
| =60 P1
| 18,88 | 9,444 | 9,444 | 9,444 | 9,444 | 9,444 | |
( )2
| 6,533 | 2,421 | 0,309 | 2,085 | 2,421 | ||
| 5,29 | 0,692 | 0,256 | 0,033 | 0,221 | 0,256 | 
|
Случайная величина χ2 (мера расхождения) независимо от вида закона распределения генеральной совокупности при (n ≥ 50) имеет распределение χ2 с числом степеней свободы r=k–l –1, где k – число интервалов после объединения; l – число параметров распределения, определенных по выборке.
В нашем примере k = 6, l = 2 (так как функция плотности распределения зависит только от двух параметров a и b), r = 6-2-1=3.
Зададим уровень значимости α=0,05 и найдем по таблице значений χ2 критическое значение для α=0,05 и r =3. Имеем 
7,8. Так как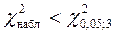 
, то предполагаемая гипотеза о равномерном законе распределения генеральной совокупности не противоречит опытным данным и принимается на уровне значимости α.
|
|
|
|
|
|
