 |
Приложение 1. Примеры кодирования информации
|
|
|
|
Кодирование информации
Цель: Изучение информационной модели канала связи и эффективного кодирования информации.
Информационные сообщения для передачи по линиям связи необходимо кодировать. Это связано с тем, что по линиям связи необходимо передавать сообщения самой различной физической природы: цифровые данные, полученные от ЭВМ, речь, тексты, телеграммы, команды управления, результаты измерения различных физических величин и т. д. Все эти сообщения предварительно должны быть преобразованы и представлены в унифицированной форме, удобной для последующей передачи.
Большинство сигналов имеют аналоговое происхождение (речь, видео). Современные системы и сети передачи данных строятся на основе цифровых каналов связи. Поэтому аналоговые сигналы подвергаются преобразованию в цифровую форму – аналого-цифровому преобразованию. Такое преобразование является примером кодирования информации.
Рассмотрим кодирование именно дискретной информации.
Упрощенная схема передачи информации по дискретному каналу связи представлена на рисунке 1.

Рис.1. Схема дискретного канала передачи информации
Источник дискретных сообщений (ИДС) использует для представления информации алфавит  . Символы исходного сообщения образуют первичный алфавит. Примером такого алфавита является латинский алфавит.
. Символы исходного сообщения образуют первичный алфавит. Примером такого алфавита является латинский алфавит.
Кодер преобразует алфавит  с объемом n символов в алфавит {a} объема m, удобный для передачи по каналу (чаще всего {a} - двоичный алфавит, включающий символы "1" и "0"). Символы, представляющие закодированное сообщение, образуют вторичный алфавит.
с объемом n символов в алфавит {a} объема m, удобный для передачи по каналу (чаще всего {a} - двоичный алфавит, включающий символы "1" и "0"). Символы, представляющие закодированное сообщение, образуют вторичный алфавит.
Правило однозначного преобразования символов первичного алфавита в символы вторичного алфавита называется кодом.
|
|
|
Основание кода (модуль) m определяется числом различимых символов в алфавите.
Простейший число-импульсный унитарный код имеет алфавит, состоящий из одних единиц, и применяется, например, в АТС для вызова абонента по телефону с помощью телефонного номеронабирателя.
Все другие коды имеют алфавит, состоящий из двух ("0" и "1") и более символов. Коды с основанием m = 2 называются двоичными или бинарным, с основанием m = 3 – троичными и т. д. При использовании в процессе кодирования электрических сигналов значение m определяет число различных градаций их амплитуды, фазы, частоты или других информативных параметров. Примеры кодов даны в Приложении 1.
В системах связи двоичные коды получили наиболее широкое применение из-за простой аппаратурной реализации устройств для передачи, опознавания и запоминания сообщений. Поэтому устройства с основанием m>2 применяются значительно реже.
Комбинация символов вторичного алфавита, соответствующая одному символу первичного алфавита, называется кодовым словом (кодовой комбинацией или вектором).
Длина кодовой комбинации – n – это разрядность кода или количество символов вторичного алфавита, необходимых для кодирования одного символа первичного алфавита. Код называется равномерным, если все кодовые комбинации одинаковы по длине (n = const), и неравномерным, если величина n в коде непостоянна (n = var).
Число кодовых комбинаций – N - в коде, каждая из которых может передавать свое отдельное сообщение. Значение N для кода с основанием m и числом элементов n определяется выражением
 (1.4)
(1.4)
Если известны N и m, то длину кодовой комбинации можно вычислить по формуле

где  -операция округления в сторону большего целого значения x
-операция округления в сторону большего целого значения x
При кодировании каждый символ первичного алфавита пронумеровывается, и передача сообщений сводится к передаче последовательности чисел (кодовых слов, составленных из символов вторичного алфавита).
|
|
|
Например, для передачи русских букв от «А» до «Я» нужно передавать числа от 1 до 32. Поэтому число кодовых комбинаций  . Если используется бинарное кодирование, то m =2. Тогда длина кодовой комбинации
. Если используется бинарное кодирование, то m =2. Тогда длина кодовой комбинации

Двоичные коды будут иметь вид
| Символ первичного алфавита | Число | Двоичный код |
| А | ||
| Б | ||
| … | … | … |
| Я |
Традиционно для кодирования одного символа используется количество информации равное 1 байту (1 байт = 8 битов). Для кодирования одного символа требуется один байт информации.
Так как каждый бит принимает значение 1 или 0, получаем, что с помощью 1 байта можно закодировать 256 различных символов. (28=256)
Кодирование заключается в том, что каждому символу ставиться в соответствие уникальный двоичный код от 00000000 до 11111111 (или десятичный код от 0 до 255).
Основные задачи кодирования:
· Снижение объема сообщения (эффективное кодирование)
· Обнаружение и исправление ошибок (помехоустойчивое кодирование)
· Защита информации от несанкционированного доступа (шифрование информации)
Для решения этих задач разработано большое количество самых разнообразных кодов.
Коды Шеннона - Фано.
При кодировании сообщений двоичным равномерным кодом, не учитывается частота символов первичного алфавита или статическая структура передаваемых сообщений. Все кодовые комбинации при этом имеют одинаковую длину.
Из первой теоремы Шеннона о кодировании сообщений в каналах без шумов следует, что если передача дискретных сообщений ведется при отсутствии помех, то всегда можно найти такой метод кодирования, при котором среднее число двоичных символов на одно сообщение будет сколь угодно близким к энтропии источника этих сообщений, но никогда не может быть меньше ее.
Учет статистики сообщений на основании теоремы Шеннона позволяет строить эффективный код, в котором часто встречающимся сообщением присваиваются более короткие кодовые комбинации, а редко встречающимся – более длинные.
Методы построения таких кодов впервые предложили одновременно в 1948-49 годах Р. Фано и К. Шеннон, поэтому код назвали кодом Шеннона-Фано.
Код строится по рассмотренным ранее правилам аналогично двоичному коду. При этом сообщения вписываются в таблицу в порядке убывания вероятности их появления. Деление на группы производится так, чтобы суммы вероятности в каждой из групп были бы по возможности одинаковыми.
|
|
|
Основной принцип, положенный в основу кодирования по методу Шеннона-Фано заключается в том, что при выборе каждой цифры кодового слова стремятся, чтобы содержащееся в ней количество информации было наибольшее. Данный код является неравномерным.
Порядок построения оптимального кода Шеннона-Фано:
1. Символы, входящие в первичный алфавит, располагаются в столбец по мере убывания их вероятностей  .
.
2. Выбирается основание кода K. (При двоичном кодировании K =2)
3. Все символы алфавита разбиваются на K групп с примерно равными суммарными вероятностями внутри каждой группы. Если равной вероятности в подгруппах достичь нельзя, то желательно чтобы суммарная вероятность нижней подгруппы была больше верхней.
4. Всем символам первой группы в качестве первого символа вторичного алфавита присваивается «0», символам второй группы – символ «1», а символам K -ой группы – символ (K – 1). Этим обеспечивается примерно равная вероятность появления всех символов 0, 1,…, K -1 на первой позиции в кодовых словах.
5. Затем каждая подгруппа аналогичным образом разбивается на подгруппы по возможности с одинаковыми вероятностями. Всем символам первых подгрупп в качестве второго символа присваивается 0, всем сообщениям вторых подгрупп – 1, а сообщениям K -ой группы – символ (K – 1).
6. Процесс продолжается до тех пор, пока в каждой подгруппе не окажется по одному символу первичного алфавита.
В качестве примера рассмотрим алфавит сообщений из 6 символов

Выполним анализ экономичности полученного кода.
Среднее количество символов вторичного алфавита на один символ первичного алфавита сообщений составляет:

Для рассмотренного примера

Если использовать простой двоичный код, то необходимое число символов 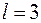 .
.
Таким образом, построенный неравномерный код будет кодировать сообщения меньшим числом символов вторичного алфавита, а значит он более эффективен.
|
|
|
Энтропия данного кода устанавливает минимально возможную длину кодовой последовательности

Для рассмотренного примера  , что соответствует утверждению первой теоремы Шеннона. Таким образом, хотя построенный код и не достигает максимально возможной эффективности, он более эффективен, чем равномерный двоичный код.
, что соответствует утверждению первой теоремы Шеннона. Таким образом, хотя построенный код и не достигает максимально возможной эффективности, он более эффективен, чем равномерный двоичный код.
Коэффициент статистического сжатия (уменьшение количества двоичных разрядов на символ сообщения при использовании статистического кодирования по сравнению с равномерным двоичным кодом) равен.

где  - максимальная энтропия кода, достигаемая при равновероятном появлении символов; m – кол-во символов.
- максимальная энтропия кода, достигаемая при равновероятном появлении символов; m – кол-во символов.
Для рассматриваемого примера

Задание
Найти эффективный код для кодирования сообщений, первичный алфавит которых образован символами собственной Фамилий Имени и Отчества. Для определения вероятностей появления символов использовать таблицу Приложения 2.
Контрольные вопросы
Чем вызвана необходимость кодирования информации?
В чем состоит кодирование?
Что такое первичный алфавит?
Что такое вторичный алфавит?
Какие символы вторичного алфавита использует двоичный код?
Что такое код?
Какую задачу решает кодер?
Какая величина называется основанием кода?
Какой код называется неравномерным?
Как определить необходимую длину кодовой комбинации, если известно количество символов первичного алфавита?
Сколько различных символов можно закодировать в 1 байте?
Каковы основные задачи кодирования?
Что утверждает первая теорема кодирования Шеннона?
Какую задачу кодирования решает код Шеннона-Фано?
Объясните алгоритм построения кода Шеннона-Фано.
В чем заключается анализ кода?
Приложение 1. Примеры кодирования информации
1. Азбука Морзе в русском варианте (алфавиту, составленному из алфавита русских заглавных букв и алфавита арабских цифр ставится в соответствие алфавит Морзе):

2. Код Трисиме (знакам латинского алфавита ставятся в соответствие комбинации из трех знаков: 1,2,3):
| А | H | O | V | ||||
| В | I | P | W | ||||
| С | J | Q | X | ||||
| В | K | R | Y | ||||
| D | L | S | Z | ||||
| F | M | T | . | ||||
| G | N | U |
|
|
|


