Главная | Обратная связь | Поможем написать вашу работу!

Комбинаторные конфигурации в алгебре и анализе

И ИХ ПРИЛОЖЕНИЯ

Комбинаторика – это область математики, в которой изучаются различные комбинации элементов дискретных (в основном – конечных) множеств, подчиненных тем или иным условиям.

Как наука комбинаторика возникла в 16 веке, и первоначально основной областью ее приложения являлись азартные игры. Однако, за последние несколько десятков лет комбинаторные методы трансформировались из разделов “досуговой” математики в инструмент решения огромного числа практически важных задач, таких как составление расписаний, планирование производства, размещение объектов на данной территории и многое другое. Не последнюю роль комбинаторика играет и при решении задач разработки технического и программного обеспечения современных информационных систем – проектирование интегральных схем, кодирование информации, организация структур данных – вот далеко не полный перечень проблем “компьютерной” математики, решаемых средствами комбинаторики.

Основные задачи, обозначения и правила

Среди многочисленных проблем, решаемых средствами комбинаторики, основное внимание уделим следующим задачам.

1. Выбор из некоторого, обычно конечного, множества некоторого подмножества (комбинации) элементов, обладающих заданными свойствами.

2. Подсчет числа таких комбинаций.

3. Определение элемента комбинации, обладающего оптимальными свойствами.

Введем следующие понятия и обозначения.

n-множество – множество из n различных элементов:

Х = {х₁, х₂, …, х_n}, х_i ¹ х_j, при i ¹ j.

(n) -множество – множество, содержащее n различных типов элементов:

Х = {х₁, х₁, …, х₁, х₂, х₂, …, х_n}.

r-выборка множества – совокупность из r элементов данного множества (если выборка из n-множества, то повторяющихся элементов нет, если из (n)-множества, то есть повторения).

Размещения – упорядоченные r-выборки (элементы прямого произведения Х₁ ´ Х₂ ´… ´ Х _r).

Сочетания – неупорядоченные r-выборки (r-элементные подмножества данного множества).

Пример 1.1.

а) На диске секретного замка 12 букв. Замок открывается после набора пароля из 5 букв.

В пароле буквы могут повторяться. Следовательно, каждый пароль – это 5-размещение из (12)-множества, т.е. размещение с повторениями.

б) Из 25 человек, членов комитета, надо выбрать: председателя, вице-председателя, секретаря и казначея (4 человека). Совмещение должностей не допускается.

В задаче повторение элементов невозможно, т.к. не допускается совмещение должностей. Кроме того, в данной 4-выборке важен порядок выбора, т.к. надо не просто выбрать заданное число человек, но необходимо связать каждого выбранного с определенной должностью. Следовательно, здесь речь идет о размещении без повторений.

в) Из 125 человек надо выбрать 6 делегатов на конференцию.

В данном случае порядок выбора не играет роли, следовательно, имеет место 6-сочетание из 125-множества.

Многие простые задачи комбинаторики решаются с помощью двух основных аксиоматических правил.

1. Правило суммы. Если все комбинации можно разбить на несколько непересекающихся классов, то общее число комбинаций равно сумме чисел комбинаций во всех классах:

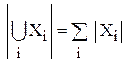2. Правило произведения. Пусть объект А можно выбрать n способами, а при каждом таком выборе объект В можно выбрать m способами. Тогда выбор упорядоченной пары (А, В) можно сделать n×m способами. В общем случае:

На практике оба правила часто используются в комбинации.

Пример 1.2. Сколькими способами можно из 28 костей домино выбрать 2 кости, которые можно приложить друг к другу?

Решение. 1-ю кость можно выбрать 28-ю способами. Из них в 7 случаях кость будет дублем, а в 21 случаях – с различными числами. Если 1-я кость является дублем, 2-ю кость можно выбрать 6-ю способами, а если – нет, то 12-ю способами. В соответствии с правилами суммы и произведения общее число случаев равно N = 7×6 + 21×12 = 294.

Простейшие конфигурации

2.1. Размещения с повторениями. Так называются упорядоченные r-выборки из (n)-множества.

Дадим более подробное определение. Пусть дано неограниченное число предметов, относящихся к n различным видам. r-размещениями с повторениями называются различные расстановки из этих предметов по r штук в каждой, образованные по следующим правилам.

1. 2 расстановки считаются различными, если они отличаются либо видом входящих в них предметов, либо порядком следования этих видов.

2. В каждую расстановку может входить несколько предметов одного вида.

Свойство. Число r-размещений с повторениями из предметов n типов обозначается и равно n^r.

Доказательство. На 1-м месте может быть предмет одного из n видов. Следовательно, существует n способов выбрать 1-й предмет. При каждом фиксированном таком способе имеется n способов выбрать 2-й предмет, и т.д. В соответствии с правилом произведения всю группу из r предметов можно выбрать n^r способами, что и требовалось доказать.

В примере 1.1.а) существует 12⁵» 250 тыс. различных паролей. (Если взломщик будет тратить по 1 секунде на проверку комбинации, то ему понадобиться 69 часов для проверки всех паролей).

Пример 1.3. В азбуке Морзе самый длинный код буквы состоит из 5 символов. Можно ли использовать коды длиной не более 4-х символов?

Решение. В соответствии с правилом суммы число различных кодов длиной не более 4 символов при использовании 2 видов символов (точка и тире) равно = 2 + 4 + 8 + 16 = 30. Значит, 4-х символьных кодов не хватит для кодирования даже всех букв кириллицы, не говоря о служебных символах. При использовании же 5-ти символьных кодов N = 30 + = 62, т.е. такой длины кода достаточно.

2.2. Размещения и перестановки без повторений. Размещениями без повторений называются упорядоченные r-выборки из n-множества. Такие расстановки по r элементов составляются из n неповторяющихся предметов.

Свойство. Число r-размещений без повторений из n предметов обозначается и равно n×(n – 1)…(n – r + 1) = .

Доказательство. 1-й предмет можно выбрать n способами, 2-й – (n – 1) способами, т.к. число кандидатов на это место уже n – 1, и т.д. В соответствии с правилом произведения получаем выражение из r сомножителей:

В примере 1.1.б) число способов выбора 4-х членов в руководство комитета из 25 человек равно = 25×24×23×22 = 303600.

В частном случае при r = n получаем = Р_n = n! Данная конфигурация называется перестановкой из n неповторяющихся предметов – упорядоченная n-выборка из n-множества.

2.3. Перестановки с повторениями. Так называют упорядоченные n-выборки из (m)-множества (n > m). Если некоторые элементы такой выборки совпадают, то могут существовать неразличимые (совпадающие) перестановки.

Найдем количество различных перестановок. Обозначим a, b,…, z – переставляемые объекты; n_j – количество повторений j-го элемента, j = 1,…,m, ; Р(n₁, n₂,…, n_m) – число таких перестановок. Рассмотрим 1-ю перестановку: .

Объекты “а” можно переставлять n₁! способами, но поскольку все они одинаковы, то такие перестановки не дают новых комбинаций. Следовательно, число действительно различных перестановок за счет совпадения первых n₁ элементов будет в n₁! раз меньше, чем в случае всех различающихся элементов. Аналогично, совпадение n₂ элементов “b” уменьшает число различных перестановок в n₂! раз, и т.д. Поскольку при несовпадении всех n элементов количество перестановок было бы равно n!, то

Р(n₁, n₂,…, n_m) = .

Пример 1.4. Найти все перестановки букв в слове “мама”.

Решение. В данном слове есть объекты 2-х типов – “м” и “а”. Всего множество содержит 4 элемента. Следовательно, число перестановок равно . Действительно, имеем следующие комбинации: ”аамм”, “мама”, “амам”, “ммаа”, “амма”, “маам”.

Пример 1.5. Найти число перестановок букв в слове “Миссисипи”.

Решение. Длина этого слова – 9 букв. Из них буква “м” встречается 1 раз, “и” – 4 раза, “с” – 3, “п” – 1. Следовательно, число перестановок равно

Р(1, 4, 3, 1) = = 2520.

2.4. Сочетания без повторений. Так называются неупорядоченные r-выборки из n-множества (r < n).

Свойство. Число r-сочетаний без повторений из n предметов обозначается и равно .

Доказательство. Каждое неупорядоченное r-сочетание можно упорядочить r! способами и получить r-размещение. Следовательно, сочетаний в r! раз меньше, чем размещений, т.е.

= Р(r, n – r).

В примере 1.1.в) 6 делегатов из 125 человек можно выбрать = 4.691×10 ⁹ способами

Пример 1.6. В лотерее из 36 номеров будут выбраны 5. Какова вероятность угадать ровно 3 номера из 5?

Решение. 3 номера из 5 верных можно выбрать способами. На каждый угаданный номер могут приходиться любые 2 из 31 невыбранных номеров, т.е. сочетаний. Окончательное число благоприятных случаев равно 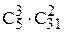. Общее же число случаев равно количеству выпадения 5 номеров из 36, т.е. .

Отсюда вероятность угадывания равна » 0.0123 – немногим более 1%.

2.5. Сочетания с повторениями. Это неупорядоченные r-выборки из (n)-множества. Они получаются, например, если необходимо r неразличимых предметов разместить по n ящикам, в частности возможно n > r.

Свойство. Число r-сочетаний с повторениями из n предметов обозначается и равно .

Доказательство. Обозначим r_j ³ 0 – количество элементов j-го типа в сочетании, (r_j можно интерпретировать как количество предметов в j-м ящике). Набор значений r_j однозначно определяет текущее сочетание. Представим этот набор в виде следующей бинарной последовательности. Числа r_j отобразим в группы из r_j единиц, каждую такую группу отделим от соседних одним нулем (если r_j = 0, то несколько нулей могут стоять подряд). Число промежутков равно n – 1. Например, набор (2, 0, 3, 1), n = 4, r = 6 соответствует последовательности (1, 1, 0, 0, 1, 1, 1, 0, 1).

Построенная конструкция – не что иное, как набор перестановок с повторениями объектов 2-х видов – 0 и 1. Число нулей в этих сочетаниях равно n – 1, а единиц – r. Следовательно, , что и требовалось доказать.

Пример 1.7. Определить количество N возможных сочетаний из 8 пирожных 4-х сортов.

Решение. В данном случае r_j– число пирожных j-го сорта. Следовательно, r = 8, n = 4 и N = = = 165.

Другой вариант доказательства основан на построении взаимно-однозначного отображения напрямую между элементами повторных и бесповторных сочетаний. Свяжем каждый набор r₁, r₂, …, r_n с элементами n – 1-сочетаний без повторений из множества чисел {1, 2,…, n + r – 1}. Обозначим К_j, j = 1,…, n –1– число, стоящее на j-м месте в отбираемом сочетании (К_j > К_j_–1), формально положим К₀ = 0. Построим взаимно-однозначное отображение

f: (r₁, r₂, …, r_n) ® (K₁, K₂, …, K_n_–1)

по следующему правилу:

r_j = К_j – К_j_{– 1} – 1, j = 1,…, n – 1; (1.1)

r_n = (n + r – 1) – К_n_–1.

Очевидно, обратное отображение строиться по формуле

К_j = 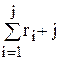, j = 1,…, n –1. (1.2)

Покажем, что числа, найденные по формулам (1.1) являются элементами r-сочетаний с повторениями. Действительно, т.к. при любом j и , то 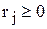. Кроме того

Несложно также убедиться, что числа К_j, полученные по формуле (1.2) являются натуральными, и обладают всеми свойствами элементов сочетаний:

;

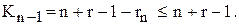
Следовательно, отображение f действительно устанавливает взаимно однозначное соответствие между элементами r-сочетания из (n)-множества и элементами n – 1-сочетания из n + r – 1-множества. Отсюда 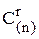= = . Последнее равенство вытекает из формулы числа сочетаний.

2.6. Свойства чисел сочетаний

1. = . Это свойство вытекает из формулы числа сочетаний.

2. = + .

Доказательство. Разобьем все r-сочетания на два класса. К первому классу отнесем сочетания, содержащие объект a_n, ко второму классу – не содержащие a_n. Так как в первом классе меняются только r – 1 элементов из n – 1 возможных, то он содержит r – 1-сочетания из n – 1-множества, следовательно, в нем элементов. Второй класс содержит все r-сочетания из n – 1-множества, т.к. в них нет одного элемента – a_n. Следовательно, в нем элементов. Общее число сочетаний, согласно правилу суммы равно + , что и требовалось доказать.

Данное свойство позволяет легко построить рекуррентный процесс вычисления всех чисел сочетаний. Положим по определению для любого n ³ 0 (ноль элементов из любого множества, в том числе – пустого, можно выбрать 1 способом, кроме того, по определению 0! = 1 – см. формулу из 2.4) и (отрицательное количество элементов выбрать невозможно). Организуем двойной цикл для вычисления всех , r £ m £ n:

for m:= 1 to n do

for r:= 0 to m do := +

Описанный процесс удобно представить в виде таблицы, называемой треугольником Паскаля:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………….

В таблице каждая m-я строка состоит из чисел , r = 0, … m, каждый элемент равен сумме двух элементов, расположенных над ним (пустое место считается нулем).

3.

Доказательство. Пусть имеем последовательность из n двоичных разрядов, содержащих 0 или 1. Очевидно, что каждую такую последовательность можно рассматривать, как n-размещение с повторениями из элементов 2-х типов, значит, количество этих размещений равно 2ⁿ.

Теперь рассмотрим некоторое множество из n объектов – а₁, … а_n, из которого будем образовывать все возможные сочетания без повторений, включая: 0-сочетания (не выбирается ни один объект), 1-сочетания и т.д., n-сочетания. При этом любую из упомянутых выше последовательностей из 0 и 1 можно интерпретировать, как перечень элементов, отбираемых в сочетание – если на k-м месте последовательности стоит 1 – элемент а_k отобран, если 0 – не отобран. Очевидно, что таким образом будут перечислены все бинарные n-последова-тельности. По правилу суммы общее число таких сочетаний, а, значит – и бинарных последовательностей равно Свойство доказано.

Замечание. Каждая отбираемая в сочетание группа элементов представляет собой некоторое подмножество исходного множества из n объектов. Следовательно, число всех подмножеств (включая пустое) множества из n элементов равно 2ⁿ.

Комбинаторные конфигурации в алгебре и анализе

Многие важные формулы алгебры и математического анализа (и других разделов математики) имеют наглядную комбинаторную интерпретацию или доказываются с использованием правил комбинаторики.

3.1. Бином Ньютона. – формула бинома Ньютона. В частности, (х + у)² = х² + 2ху + у²; (х + у)³ = х³ + 3х²у + 3ху² + у³ и т.д.

Доказательство. Раскроем скобки выражения (х + у)ⁿ = (x + y)(x + y)…(x + y). В результате получим сумму членов вида . Например (х + у)³ = ххх + хху + хух + хуу + ухх + уху + уух + ууу. Приведем подобные члены, подсчитав число таких произведений при каждом k = 0,…, n. Каждое такое выражение – не что иное, как перестановка повторениями из 2-х элементов. Полагая n₁ = k, n₂ = n – k, получим, что число этих перестановок равно Р(k, n – k) = (см. пп. 2.3, 2.4), т.е. множитель при х^kуⁿ^–^k совпадает с , что и требовалось доказать.

С помощью формулы бинома легко получить новые свойства чисел сочетаний.

5. . Доказать легко с использованием бинома Ньютона на основе тождества (1 – 1)ⁿ = 0.

6. .

Доказательство. Имеем: n×2ⁿ^–1 = n×(1 + 1)ⁿ^–1 = . В свою очередь при любом р выполняется равенство:

= = .

Следовательно, . Переобозначим индекс суммирования, положив p + 1 = k. Имеем:

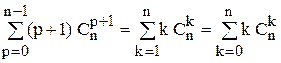что и требовалось доказать. В последнем равенстве формально введено равное нулю слагаемое при k = 0.

3.2. Полиномиальная формула. Формулу бинома можно обобщить на случай нескольких слагаемых: (х₁ + х₂ + … + х_k)ⁿ.

Запишем эту формулу в виде произведения одинаковых сомножителей и перемножим. Получим все возможные n-размещения с повторениями из объектов х₁, х₂, …, х_k. Приведем подобные, сосчитав число повторений каждого слагаемого вида . Для этого надо определить число слагаемых, в которых символ х₁ повторяется n₁ раз, х₂ – n₂ раз, и т.д., х_k повторяется n_k раз. Каждое такое слагаемое – это перестановка с повторением n_j раз элемента х_j, j = 1,…k. Число таких перестановок равно Р(n₁, n₂,…, n_k), å n_j = n. Следовательно

(х₁ + х₂ + … + х_k)ⁿ = .

Выражение n₁ + … + n_k = n в значке суммы означает, что перебираются все (целые неотрицательные) значения n₁,…, n_k, удовлетворяющие данному условию.

Например: (x + y + z)⁴ = P(4, 0, 0)×x⁴ + P(0, 4, 0)×y⁴ + P(0, 0, 4)×z⁴ + P(3, 1, 0)×x³y + P(3, 0, 1)×x³z + P(2, 2, 0)×x² y² + P(2, 1, 1)×x² y z + P(2, 0, 2)×x² z² + P(1, 3, 0)×x y³ + P(1, 0, 3)×x z³ + P(1, 1, 2)×x y z² + P(1, 2, 1)×x y²z + P(0, 3, 1)×y³ z + P(0, 1, 3)×y z³ + P(0, 2, 2)×y² z².

Напоминаем, что здесь Р(a, b, c) = , например Р(2, 1, 1) = = 12.

3.3. Ряд Ньютона. Формулу бинома можно обобщить на случай нецелой степени, в результате получим выражение:

(у + х)ⁿ = уⁿ+ n уⁿ^–1х + + … + + +…

При целом значении n формула содержит конечное число слагаемых, т.к. для k > n коэффициенты при уⁿ^–^kх^k обращаются в ноль. При нецелом n получается бесконечный степенной ряд. Найдем радиус его сходимости. Представим бином в виде:

(у + х)ⁿ = = уⁿ (1 + z)ⁿ=

уⁿ .

Воспользуемся формулой Даламбера:

, где .

Имеем: 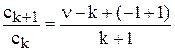= –1 + ® – 1. Отсюда R = 1. Следовательно, ряд сходится при |z| < 1, т.е. при |x| < |y|. Если разложение в ряд происходит по степеням у, то ряд сходится при |у| < |х|.

Пример 1.8. = (1 – х)^–1 = 1 + (– 1)×(– х) +

+ = 1 + х + х² +…

– формула бесконечно убывающей геометрической прогрессии, которая сходится при |x| < 1.

Тема 2. Комбинаторные алгоритмы

При поиске оптимального варианта из некоторого допустимого набора часто приходится перебирать все возможные альтернативы. Во многих задачах перебираемые варианты являются членами сочетаний, размещений и других комбинаторных конфигураций. Поэтому большое значение имеют алгоритмы генерации элементов соответствующих конечных множеств.

Главная сложность составления таких ”генераторов” состоит в необходимости сделать их структуру независимой от размерности порождаемых ими множеств, которая может очень сильно варьироваться в различных задачах. Например, алгоритм генерации r-размещений с повторениями очень легко реализовать с помощью r вложенных циклов:

for j1:= 1 to n do

for j2:= 1 to n do

…………………..

for jR:= 1 to n do writeln (j1, j2, … jR);

Ясно, что всякий раз при изменении значения r такую программу пришлось бы переделывать, добавляя или удаляя циклы, и на самом деле алгоритм генерации должен быть другим.

Другой особенностью предлагаемых алгоритмов является то, что в них вместо комбинаций самих объектов генерируются комбинации из их номеров. Очевидно, что такие расстановки легко преобразовать в манипуляции, например, с названиями объектов, введя в программу массив из строк символов соответствующей размерности.

Многие из комбинаторных конфигураций удобно генерировать с помощью алгоритма поиска с возвратом.

Общая схема рекурсивного поиска с возвратом. Пусть дано n упорядоченных множеств В₁, В₂,… В_n. Требуется найти набор векторов вида Х = (х₁, х₂,… х_n), где x_iÎВ_i, удовлетворяющих некоторым дополнительным условиям. Иными словами Х Î В₁´В₂ ´… ´В_n.

В алгоритме поиска с возвратом каждый вектор Х строится покомпонентно слева направо. Предположим, что уже найдены первые k – 1 компонент х₁, х₂,… х_k_–₁. Тогда их значения определяют некий набор условий, ограничивающих выбор k-й компоненты некоторым множеством S_k Í В_k. Если S_k не пусто, мы вправе выбрать в качестве х_k первый по порядку элемент из S_k, присоединить его к уже выбранным компонентам, и перейти к выбору х_k₊₁ и так далее. Однако, если набор условий таков, что S_k пусто, то мы возвращаемся к выбору k–1-й компоненты. При этом мы отбрасываем х_k_–₁ и выбираем в качестве новой k–1-й составляющей вектора Х тот элемент из S_k_–₁, который непосредственно следует за только что отброшенным х_k_–₁.

Предположим теперь, что в процессе поиска новых компонент мы дошли до конца, т.е. выбрали х_n. Теперь надо как-то использовать полученный вектор Х, в соответствие с условием задачи. Например, если в задаче требуется найти лучший из векторов, то нам следует сравнить построенный вектор Х с решением, которое до данного момента считалось оптимальным и если Х окажется лучше, то надо обновить текущее оптимальное решение, вернуться на шаг назад и продолжить поиски новых решений.

Этот процесс продолжается, пока не будут рассмотрены все возможные вектора решений.

Данная схема легко реализуется посредством рекурсивной процедуры.

procedure Solve (k);

{ k – номер подбираемой координаты (номер глубины рекурсии) }

{ Х – вектор текущего решения }

begin if á Х – решение ñ then á Использовать Х ñ

Else

begin á Определить S_k ñ;

for у Î S_k do

begin X_k:= y;

á Сузить S_k₊₁ с учетом выбранного X_k ñ;

Solve(k+1);

S_k:= S_k \ {y};

á Расширить S_k₊₁ с учётом сужения S_k ñ;

end;

{ Головная программа }

begin Solve (1);

End.

Конкретный набор требований, которым должны удовлетворять сгенерированные векторы, определяются множествами S_k, а также правилом проверки того, что Х – решение.

1. Алгоритм генерации r-размещений с повторениями. В размещениях с повторениями на k-месте должно стоять число из набора 1,…, n независимо от чисел, стоящих на предыдущих позициях. То есть для любого k всегда будет S_k= {1, …, n }.

Пример 2.1. Пусть r = 3; n =2. Надо получить следующие векторы Х: (1 1 1), (1 1 2), (1 2 1), (1 2 2), (2 1 1), … (2 2 2).

Обозначим А[j] – номер предмета, находящегося на j-м месте, j = 1,…r. Предлагается следующий алгоритм.

Procedure Razm_P(k);

Begin

if k=r+1 then write(A[1],…A[r]);

Else

for y:=1 to n do

begin A[k]:=y; Razm_P(k+1);

end;

Begin

Razm_P(1);

End.

Назначение процедуры Razm_P(k) – получение k-й компоненты вектора Х =(A[1],…A[r]). Если k = r+1 – это означает, что вектор полностью получен, и надо его использовать (вывести на экран). В противном случае надо получить следующую компоненту. Так как на ее месте может стоять любое число от 1 до n, то S_k = {1, … n}, перебор элементов этого множества обеспечивается циклом for y:=1 to n do

2. Алгоритм генерации r-размещений без повторений. Отличие данного алгоритма от предыдущего в том, что каждое из возможных значений 1, … n элементов размещений можно использовать только один раз. Поэтому в процедуре Razm_BP используется массив dop[j], j = 1,…n, в котором dop[j] = 1, если значение j не было использовано и dop[j] = 0, в противном случае. При продвижении вглубь рекурсии значение j блокируется, чтобы его нельзя было использовать повторно, а при откате – восстанавливается.

Procedure Razm_BP(k);

Begin

if k=r+1 then write(A[1],…A[r]);

Else

for y:=1 to n do

if dop[y] > 0 then

begin A[k]:=y; dop[y]:=dop[y]-1;

Razm_BP(k+1); dop[y]:=dop[y]+1;

end;

begin for i:=1 to n do dop[i]:= 1;

Razm_BP(1);

End.

Данный алгоритм можно также использовать для генерации перестановок без повторений при r = n.

3. Алгоритм генерации перестановок с повторениями. Этот алгоритм похож на предыдущий, только первоначально dop[j]=n[j] – число повторений j-го значения, j = 1,…m. По мере использования этого значения переменная dop[j] уменьшается, пока не станет равной 0. Это будет означать, что данное значение уже нельзя использовать. Предлагается следующий алгоритм генерации перестановок из m объектов при .

Procedure Perest_P(k);

begin if k=n0+1 then write(P[1],…P[n0]);

Else

for y:=1 to m do

if dop[y] > 0 then

begin P[k]:=y; dop[y]:=dop[y]-1;

Lex(k+1); dop[y]:=dop[y]+1;

end;

begin n0=0;

for j:=1 to m do

begin dop[j]:=n[j]; n0:=n0+n[j]; end;

Lex(1);

End.

4. Алгоритм генерации r-сочетаний без повторений. Алгоритм похож на генерацию размещений без повторений, отличие в том, что в каждом сочетании не допускаются перестановки элементов, т.е. каждый следующий элемент больше предыдущего.

Пример 2.2. Подобные 3-сочетания из 5 выглядят так: (1 2 3), (1 2 4), (1 2 5), (1 3 4), … (1 4 5), (2 3 4), … – т.е. генерируется возрастающая последовательность 3-значных чисел.

Для обеспечения этого условия в генерации сочетаний используется цикл for y:=t to n do, а не for y:=1 to n do, как в размещениях, где переменная t подбирается по правилу if k<=1 then t:=1 else t:=А[k-1]+1.

Procedure Sochet_BP(k);

begin if k=r+1 then write(А[1],…А[r]);

Else

begin if k<=1 then t:=1 else t:=А[k-1]+1;

for y:=t to n do

if dop[y] > 0 then

begin А[k]:=y; dop[y]:=dop[y]-1;

Sochet_BP(k+1);

dop[y]:=dop[y]+1;

end;

begin for i:=1 to n do dop[i]:= 1;

Sochet_BP(1);

End.

5. Разгадка числовых ребусов. В числовых ребусах зашифровывают некоторое арифметическое действие, буквами обозначают цифры. Разным цифрам соответствуют разные буквы. Требуется разгадать, какая цифра скрывается за каждой буквой. Это возможно, если воспользоваться программой генерации размещений без повторений.

Пример 2.3. ТОРГ ´ Г = ГРОТ. Имеем 4 различных цифры: Т, О, Р, Г. Следовательно, необходимо сгенерировать 4-размещения из 10 (всего 10 цифр), т.е. массив а[1], …, а[4], удовлетворяющий следующим условиям:

1) а[1] ¹ 0, а[4] ¹ 0 – т.к. число не может начинаться с 0.

2) (а[1]×1000 + а[2]×100 + а[3]×10 + а[4])×a[4] = а[4]×1000 + а[3]∙100 + а[2]∙10 + а[1] – это запись зашифрованного действия.

В процессе генерации каждое полученное сочетание проверяют на выполнение перечисленных условий и отбирают подходящие. В общем случае решений может быть несколько. В данном примере ТОРГ = 1089 (1089×9 = 9801).

Тема 3. АНАЛИТИЧЕСКИЙ АППАРАТ

КОМБИНАТОРИКИ

Формулы и алгоритмы, рассмотренные в теме 1, дают способы вычисления комбинаторных чисел для некоторых распространенных конфигураций. Однако практические задачи далеко не всегда непосредственно сводятся к ним. В этом случае чрезвычайно важно знание методов сведения одних конфигураций к другим, либо общих методов, не столь зависящих от конкретных комбинаторных структур. Рассмотрим наиболее популярные из таких методов.

12 Следующая ⇒

Воспользуйтесь поиском по сайту: