Главная | Обратная связь | Поможем написать вашу работу!

Задания для самостоятельного выполнения

ЛАБОРАТОРНАЯ РАБОТА №5

РАСТРОВАЯ ГРАФИКА

Во всех графических режимах видеопамять (ВП) организована как образ (подобие) растра экрана видеомонитора (ВМ). Это означает, что каждому пикселю графического экрана поставлена в соответствие некоторая ячейка ВП. Каждая ячейка хранит значения атрибута пикселя – информацию о яркости и цвете.

В растровой графике любой графический примитив (отрезок прямой, дуга окружности, любая аналитическая кривая, частично или целиком, в дальнейшем их будем называть векторами) моделируется на экране как последовательность точек в узлах сетки растра. При этом для каждой точки устанавливается адрес соответствующей ячейки ВП и туда записывается атрибут точки вектора. Таким образом, задача формирования видеокода вектора складывается из задачи нахождения точек в узлах сетки растра (моделирующих заданный вектор), вычислении соответствующих адресов ячеек ВП и записи по этим адресам атрибутов точек вектора.

Существует несколько способов построения растровых изображений векторов. Наиболее распространенный из них алгоритм Брозенхейма. Рассмотрим упрощенную модификацию такого алгоритма, который известен как метод оценочной функции.

Воспроизведение отрезка прямой линии. Поскольку точки растра формируются последовательно, то шаг в очередную точку можно рассматривать как движение по узлам сетки растра, а движущуюся точку будем называть изображающей точкой (ИТ). В дальнейшем будем изучать движение ИТ в xoy с шагом 1. Рассмотрим случай, когда отрезок задан в первой четверти (рис.1).

Уравнение прямой, на которой лежит заданный отрезок(A, B), имеет вид:

Ay – Bx =0.

Введем оценочную функцию таким образом: F (x, y) =Ay – Bx.

Оценочная функция обладает такими очевидными свойствами:

F (x, y) = 0, если точка (x, y) лежит на прямой;

F (x, y) > 0, если точка (x, y) выше прямой;

F (x, y)< 0, если точка (x, y) ниже прямой.

Движение ИТ должно сводиться к последовательному прохождению через узлы сетки, начиная с x =0, y =0, так, чтобы по возможности меньше отклоняться от заданной прямой и на определенном шаге движения попасть в точности в положение x = A, y = B. Такая задача получила в технических приложениях известность как задача интерполяции, а один шаг движения при этом реализуется одним циклом интерполяции. Решается эта задача использованием свойств F (x, y), из которых следует, что если в результате предыдущего шага ИТ оказалась в точке (x, y) то решение о следующем шаге следует принимать по правилам:

если F (x, y) < 0, то y:= y +1, делается шаг +1 по y;

если F (x, y) > 0, то x:= x +1, делается шаг +1 по x;

если F (x, y) = 0, то x:= x +1 при A ³ B; и y:= y +1 при A < B.

Движение начинается с начальными условиями x =0, y =0, F (x, y) =0 и заканчивается при x = A, y = B. После выполнения A + B циклов интерполяции ИТ окажется в точке (A, B).

Изложенный алгоритм предполагает вычисление F (x, y)в каждом цикле интерполяции. Эти вычисления могут выполняться следующим образом:

после шага равного +1 по координате X:

F (x +1, y)= Ay – B (x +1) = Ay – Bx – B = F (x, y) – B;

после шага равного +1 по координате Y:

F (x, y +1)= A (y + 1) – Bx = Ay + A – Bx = F (x, y)+ A.

Воспроизведение дуги окружности. Рассмотрим случай, представленный на рис. 2, когда дуга окружности в 1-й четверти, движение осуществляется против часовой стрелки от (x_H, y_H) до (x_K, y_K).

Уравнение окружности x ²+ y ² = R ², R – радиус окружности. Оценочная функция: F (x, y) = x ² + y ² – R ².

Свойства F (x, y):

F (x, y) = 0, если точка (x, y) лежит на окружности;

F (x, y) > 0, если точка (x, y) вне окружности;

F (x, y)< 0, если точка (x, y) внутри окружности.

Правила принятия решения об очередном шаге (для случая движения против часовой стрелки по дуге, заданной в первой четверти):

если F (x, y) < 0, то y:= y + 1, делается шаг +1 по y;

если F (x, y) > 0, то x:= x – 1, делается шаг –1 по x;

если F (x, y) = 0, то x:= x – 1 при x £ y и y:= y + 1 при x > y.

Движение начинается с начальными условиями x = x_H, y = y_H, F (x, y)=0 и заканчивается при x = x_K, y = y_K. Оценочная функция вычисляется в каждом цикле интерполяции по формулам:

F (x, y +1) = x ²+(y +1)² – R ² = F (x, y) +2 y +1;

F (x –1, y) = F (x, y) – 2 x +1.

Изложенный метод прост в реализации и позволяет обойтись только целочисленной арифметикой. Недостаток – необходимость в большом количестве модификаций алгоритма даже при воспроизведении одного вектора, но c разными начальными условиями.

Другой метод – метод цифровых дифференциальных анализаторов (ЦДА), основан на численном решении дифференциального уравнения движения точки по заданной кривой. Модель движения ИТ примем такой, как это показано на рис.3.

Описание движения ИТ по заданной кривой будет иметь вид:

x_i ₊₁ = x_i +D x_i,

y_i ₊₁ = y_i +D y_i,

i =1,2,...,

x ₀= x_н, y ₀= y_н.

Один цикл движения назовем циклом интерполяции. На D x_i и D y_i наложим такое условие – за один цикл интерполяции результирующее движение должно быть: D l_i £ 1. При выполнении данного условия теоретический шаг движения никогда не превысит единицы по каждой координате (следовательно, ни при каком цикле интерполяции не произойдет «перепрыгивания» через очередную точку растра).

Введем переменные X_i, Y_i – это ближайшие целые значения координат точного положения движущейся точки после очередного цикла интерполяции, т.е. это координаты точек растра.

С учетом изложенного, модель движения по узлам сетки с единичными шагами будет иметь вид:

x_i ₊₁ = x_i +D x_i,

X_i ₊₁ = (int) x_i ₊₁,

y_i ₊₁ = y_i +D y_i,

Y _i+1 = (int) y_i ₊₁,

, при i =1,2,..., x ₀= x_н, y ₀= y_н.

Операцию (int) y_i ₊₁ будем понимать как взятие ближайшего целого от y_i ₊₁.

Если реализуется указанная модель движения и циклы интерполяции выполняются с интервалом D t = 1/ F, то скорость движения ИТ по кривой будет v = 1/D t = F, где F – частота выполнения циклов интерполяции.

Пусть кривая задана уравнением в неявной форме F (x, y)=0,а v есть скорость движения ИТ по этой кривой. Если F (x, y)=0, то 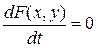и

Очевидно, что

, или , ,

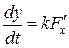где 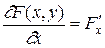, , 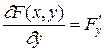обращают в нуль левую часть уравнения при всех (x, y), удовлетворяющих F (x,y)=0. Следовательно получены дифференциальные уравнения движения по кривой F (x,y)=0, а k – произвольный коэффициент, задающий направление и скорость движения.

При малых D t возможен переход к конечным разностям

и .

Тогда , . Для выбора D t примем, что 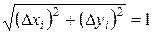, т.е.

, , .

Приведем возможную реализацию этого метода на примере окружности. Уравнение окружности в форме F (x, y)=0 имеет вид:

F (x, y) = x ² + y ² – R ².

При этом , , . Тогда

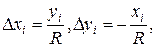
Изложенный алгоритм обеспечивает воспроизведение участка кривой длинной D l_i = 1 за один цикл интерполяции. При частоте интерполяции F вектор строится со скоростью v = F ед./сек. Изменяя F, можно управлять скоростью построения вектора. Для этого положим , что соответствует и 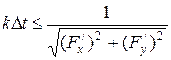. Выберем , где m – наименьшее целое, для которого выполняется , т.е. 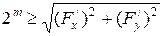. Тогда , . В этом случае, простота вычислений внутри цикла интерполяции делает этот алгоритм более эффективным.

Задания для самостоятельного выполнения

Методами оценочной функции и ЦДА построить заданную линию.

1. Отрезок прямой в заданной четверти в указанном направлении.

2. Дуга окружности в заданной четверти в указанном направлении.

3. y = 2 px.

4. .

5. x = – ay.

6. y ²= axy + bc.

Воспользуйтесь поиском по сайту: