 |
Это означает, что интервал любой прямой, лежащей в плоскости, больше интервала масштаба уклона или равен ему.
|
|
|
|
Рассмотрим случаи, когда требуется в заданной плоскости провести прямую с заданным уклоном и через данную прямую провести плоскость с заданным уклоном.
Пусть через точку А7, лежащую в плоскости Σi (рисунок 16) требуется провести прямую с заданным уклоном i = 1:2. Для этого из точки А как из центра проведем окружность с радиусом R, равным интервалу прямой заданного уклона.
i = 1:2.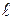 
= 2 R = 2 ед
В пересечении ее с соседними горизонталями обозначим КМ и NL. Прямые MN и KL, проходящие через точку А, лежат в плоскости Σ и имеют заданный уклон. Задача имеет два решения.
На рисунке 17 Решена обратная задача: через прямую АВ проведены плоскости Σ и Ω с заданным уклоном (задача тоже имеет два решения)
i = 1:2
= 2
Горизонтали плоскости с целочисленными отметками должны проходить через точки прямой, имеющие так же отметки и проекции этих горизонталей должны быть расположены на расстояниях, равных интервалу масштаба уклонов плоскости.
Для решения задачи выполняем следующие построения. Из точки, лежащей на прямой и имеющей целочисленную отметку, например, из точки 4, как из центра опишем дугу окружности с радиусом R, равным заданному интервалу масштаба уклона плоскости.
Рисунок 16
Рисунок 17
Из соседней точки с отметкой 3 проводим касательные к окружности, которые будут являться горизонталями плоскостей Σ и Ω. Остальные горизонтали плоскости проходят параллельно полученным через точки прямой, имеющие целочисленные отметки.
Масштабы уклонов плоскостей перпендикулярны горизонталям.
3.2. Проекции многогранников
Применяя метод проекций с числовыми отметками для изображения геометрических тел, необходимо на проекции данного тела указывать отметки характерных точек и линий.
|
|
|
В многограннике характерными точками являются его вершины.
На рисунке 16 дана проекция S, A, B, C пирамиды SABC, основание которой расположено в плоскости По, а вершина отстоит от нее на 3 м.
Рисунок 18 Рисунок19
3.3. Проекции кривых поверхностей
Если задана кривая поверхность, то для ее изображения в проекциях с числовыми отметками прибегают к горизонталям, представляющим собой линии пересечения поверхности плоскостями, параллельными П0 и отстоящими друг от друга на единицу высоты.
На рисунке 19 изображен прямой круговой конус, стоящий основанием на плоскости П0. Проекцией конуса являются концентрические окружности с числовыми отметками.
Кривые поверхности в проекциях с числовыми отметками задаются проекциями их горизонталей с числовыми отметками.
Такой способ задания поверхности является наиболее удобным для изображения неправильных поверхностей, так называемых графических или в применении к земной поверхности – топографических. По отметкам горизонталей можно судить о форме изображенной поверхности.
Рисунок 20
Так, на рисунке 20 изображена котловина, низшая горизонталь которой имеет отметку 7.
3.4. Поверхность одинакового ската
Поверхностью одинакового ската называется линейчатая
поверхность, все прямолинейные образующие которой составляют с плоскостью одинаковый угол.
Если прямой круговой конус перемещать так, чтобы его вершина скользила по некоторой направляющей MN, а его ось оставалось перпендикулярной к горизонтальной плоскости, то поверхность, обвертывающая различные положения конуса, будет являться поверхностью одинакового ската (рисунок 21).
Рисунок 21
Если на поверхности одинакового ската провести горизонтали этой поверхности, то они будут касаться соответствующих сечений круговых конусов, расположенных на определенных отметках.
|
|
|
На рисунке 22 показано построение горизонталей поверхности одинакового ската в проекциях с числовыми отметками.
Поверхности откосов, насыпей и выемок криволинейных участков дорог на подъемах и спусках представляют собой поверхности одинакового ската.
Рисунок 22
4. РЕШЕНИЕ ПОЗИЦИОННЫХ ЗАДАЧ
4.1. Пересечение двух поверхностей
Построение линии пересечения двух поверхностей в проекциях с числовыми отметками основано на общем методе вспомогательных секущих поверхностей. В качестве вспомогательных секущих поверхностей применяются горизонтальные плоскости.
Практически вспомогательные плоскости только подразумеваются, а на чертеже проводятся или используются готовые горизонтали поверхностей.
Порядок построения линии пересечения поверхностей:
- провести проекции горизонталей обеих пересекающихся
поверхностей;
- определить точки пересечения горизонталей одной поверхности с горизонталями другой поверхности, имеющими одинаковы отметки;
- полученные точки пересечения последовательно соединить линией, которая и будет искомой линией пересечения поверхностей.
Пример 1. Пересечение двух плоскостей (рисунок 23)
Для определения линии пересечения двух плоскостей достаточно определить точки пересечения двух горизонталей одной плоскости с двумя горизонталями, имеющими одинаковые отметки, другой плоскости и соединить прямой линией.
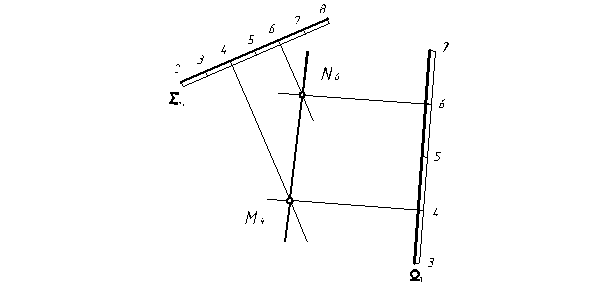
Рисунок 23
Пример 2. Пересечение плоскости и поверхности.
На рисунке 24 построена линия пересечения плоскости Σ и прямого кругового конуса.
Линия пересечения – эллипс – построен как результат пересечения горизонталей (прямых) плоскости с горизонталями конуса, имеющими одинаковые отметки (окружностей).
Рисунок 24
4.2. Пересечение прямой с поверхностью
Пересечение прямой с поверхностью в проекциях с числовыми отметками основано на общем методе вспомогательной секущей плоскости.
Порядок построения точек пересечения прямой с поверхностью:
- через прямую провести вспомогательную секущую плоскость общего положения, задав ее проекциями горизонталей;
|
|
|
- остроить линию пересечения данной поверхности и вспомогательной плоскости;
- определить точки пересечения прямой и полученной линии
пересечения.
Пример 1. Пересечение прямой и топографической поверхности (рисунок 25).
Построены точки пересечения MN прямой AB с топографическойповерхностью.
Проградуировав прямую АВ, проведем через нее плоскость общего положения, заданную проекциями горизонталей. Построена линия пересечения плоскости и поверхности. Определены точки M и N пересечения прямой АВ и полученной линии пересечения.
Рисунок 25
4.3. Примеры из инженерной практики
Пример 1. Определение границ насыпи и выемки на строительной площадке.
Пусть требуется определить границы земляных работ для создания горизонтальной строительной площадки с отметкой
+ 60 м, контур которой изображен на рисунке 27.
Уклоны откосов выемки iB = 1:1, насыпи IH = 1:1.5.
Прямоугольный въезд на площадку – аппарель имеет уклон i 
= 1:4.
Линия нулевых работ пройдет по 60-й горизонтали местности.
Часть площадки окажется в выемке, часть – на насыпи. Искомые границы земляных работ представляют собой линии пересечения топографической поверхности с откосами насыпей и выемок. Чтобы определить эти линии, необходимо построить горизонтали всех откосов.
Интервал выемок LB = 
= 1 м.
Интервал насыпей LН =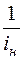 
= 1,5
Интервал аппарели LА = 
= 4 м
Горизонтали откосов будут прямыми линиями, параллельными соответствующим сторонам площадки.
Горизонтали аппарели строятся с учетом того, что они проходят через наклонные бровки (см. 3.1.1 рисунок 17).
В результате каждая плоскость откосов выемки и насыпи изображена своими горизонталями. Остается построить линии пересечения этих плоскостей друг с другом и с поверхностью земли. Искомые линии определяются точками пересечения горизонталей с одинаковыми отметками рассматриваемых плоскостей и поверхности земли.
Пример 2. Дана топографическая поверхность. Построить ее профиль по лини А-А (рисунок 26). В инженерно-строительном деле профилем называется вертикальное сечение поверхности.
|
|
|
Секущая плоскость перпендикулярна плоскости П0. Она пересекает горизонтали в точках В, С,... F. Для построения профиля совместим секущую плоскость вместе с точками В, С,... F с плоскостью П0 . Для этого построим горизонтали с отметками 4,5.... 10 и каждую точку пересечения проецируем на горизонталь с одинаковой отметкой
Полученные точки В,С....F соединим кривой линией, которая и будет искомым профилем поверхности по линии А-А.
Рисунок 26
ЛИТЕРАТУРА
1. Кузнецов Н.С. Начертательная геометрия. – М.: Высшая школа, 1981.
2. Русскевич Н.Д. Начертательная геометрия. – Киев: Буденильник. 1970.
3. Сборник задач по начертательной геометрии. Под редакцией профессора Н.Д. Русскевича. – Киев: Вища школа, 1978.
4. Крылов Н.Н., Иконников Г.С., Николаев В.А. и др. Под редакцией Н.Н. Крылова. Начертательная геометрия – М., 1984.
5. Винницкий И.Г. Начертательная геометрия – М., 1975.
СОДЕРЖАНИЕ
1. Сущность метода. Проекции точек…………………………..3
2. Проекции прямых линий…………………………………….. 4
2.1. Взаимное положение двух прямых линий……………... 6
3. Проекции плоскостей…………………………………………..
3.1. Проекции плоскостей……………………………………. 7
3.1.1. Прямая в плоскости…………………………………... 10
3.2. Проекции многогранников…………………………….. 12
3.3. Проекции кривых поверхностей………………………. 13
3.4. Поверхность одинакового ската………………………..13
4. Решение позиционных задач…………………………………...
4.1. Пересечение двух поверхностей………………………..15
4.2. Пересечение прямой с поверхностью………………….16
4.3. Примеры из инженерной практики…………………….17
5. Литература…………………………………………………… 22
|
|
|
