 |
Основные теоретические положения.
|
|
|
|
С.О. Волощук
МЕТОДИЧНИЙ ПОСІБНИК
ДО ЛАБОРАТОРНОЇ РОБОТИ №1
з навчальної дисципліни
« Теорія інформації та кодування »
Маріуполь, 2011
УДК 519.72(072)
Методические указания к лабораторным работам и практическим занятиям по курсу "Теория информации и кодирование" "Сжатие данных (кодирование текстовой информации алгоритмами Хаффмана и Лемпеля-Зива)" (для студентов специальности 7.080201 - "Информатика"). /Сост.: С.А. Волощук. – Мариуполь: ПГТУ, 2010 – 20с.
В пособии изложены основные элементы кодирования текстовой информации методами архивации без потерь: Хаффмана, Шеннона-Фано и Лемпеля-Зива. Рассмотрен пример решения задачи.
Рецензенты:
ст. пр. Алешин С.В.
доц., к.ф.-м.н. Гранкин Д.В.
Укладач:
ст. пр. Волощук С.А.
Ответственный за выпуск:
доцент, Чичкарев Е.А.
Схвалено на засіданні кафедри інформатики
«14» 11.2011, протокол № 5
Погоджено навчально-методичною комісією факультету
«01» 12.2011, протокол № 3
Лабораторная работа № 1
Кодирование текстовой информации методами архивации без потерь: Хаффмана, Шеннона-Фано и Лемпеля-Зива.
Цель работы: научиться кодировать текстовую информацию методами архивации без потерь: Хаффмана, Шеннона-Фано и Лемпеля-Зива и выполнять обратный процесс - декодирования.
Основные теоретические положения
Коды появились в глубокой древности в виде криптограмм, когда ими пользовались для засекречивания важного сообщения от тех, кому оно не было предназначено. Еще знаменитый греческий историк Геродот (V век до н.э.) приводил примеры писем, понятных лишь для одного адресата. Спартанцы имели специальный механический прибор, при помощи которого важные сообщения можно было писать особым способом, обеспечивающим сохранение тайны. Собственная секретная азбука была у Юлия Цезаря. В средние века и эпоху Возрождения над изобретением тайных шифров трудились философ Фрэнсис Бэкон, крупные математики того времени Франсуа Виет, Джероламо Кардано, Джон Валлис.
|
|
|
В этом разделе речь будет идти в основном об ином направлении в кодировании, которое возникло в близкую к нам эпоху. Связано оно с проблемой передачи сообщений по линиям связи, без которых (телеграфа, телефона, радио, телевидения и т.д.) немыслимо наше нынешнее существование. Задачей такого кодирования является сделать передачу сообщений быстрой, удобной и надежной. Предназначенное для этой цели кодирующее устройство сопоставляет каждому символу передаваемого текста, а иногда и целым словам или фразам (сообщениям) определенную комбинацию сигналов (применяемую для передачи по данному каналу связи), называемую кодом или кодовым словом. При этом операцию перевода сообщений в определенные последовательности сигналов называют кодированием, а обратную операцию, восстанавливающую по принятым сигналам (кодовым словам) передаваемые сообщения, - декодированием.
Исторически первый код, предназначенный для передачи сообщений, связан с именем изобретателя телеграфного аппарата Сэмюэля Морзе и известен как азбука Морзе. В этом коде каждой букве или цифре сопоставляется своя последовательность из кратковременных (называемых точками) и длительных (тире) импульсов тока, разделяемых паузами. Другой код, столь же распространенный в телеграфии (код Бодо), использует для кодирования два элементарных символа - импульс и паузу, при этом сопоставляемые буквам кодовые слова состоят из пяти таких сигналов.
Общая схема передачи сообщений представлена на рис.1.
|
|
|
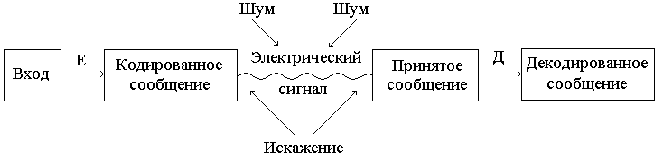
Рис. 1. Общая схема передачи сообщений.
Коды, использующие два различных элементарных сигнала, называются двоичными. Удобно обозначать эти два сигнала 0 и 1. Тогда кодовые слова можно представлять как последовательность из нулей и единиц.
Пример 1. Как можно закодировать четыре сообщения a, b, c, d, используя только два сигнала, 0 и 1?
Решение. Один из вариантов кодирования может быть следующим: 00, 01, 10, 11. При таком кодировании вероятность появления сообщений не учитывалась или предполагалась равновероятность (p=0,25). Между тем их появление в информационном тексте может происходить с различной частотой; предположим, вероятности появления сообщений равны: p=0,4; p=0,3; p=0,2; p=0,1.
Учитывая вероятность сообщений, Фано предложил следующее оптимальное кодирование
| Сообщения | a | b | c | d |
| Коды |
Показателем экономичности кода служит средняя длина кодового слова (математическое ожидание длины кодового слова). Для кодировки сообщений первым способом средняя длина равна 2, а по методу Фано - 1,75. Следовательно, закодированный по методике Фано информационный текст окажется короче.
На первый взгляд, кодирование по методу Фано кажется избыточным, поскольку представленные коды можно сократить, например, так
| Сообщения | a | b | c | d |
| Коды |
Однако если возьмем следующий закодированный текст: 011001, то по последней таблице данный текст не может быть однозначно дешифрован, так как непонятно, что, собственно, подразумевается: сообщение cada или саbbа, или baada и т.д. Расшифровка же текста по методу Фано однозначна - bac. Такой код называется префиксным. Никакое кодовое слово префиксного кода не является началом другого кодового слова. Наряду с кодом Фано, существует префиксное кодирование по методу Хаффмана, экономность которого еще выше.
Пусть двоичные сигналы 0, 1 последовательно передаются по каналу связи на приемник, тогда вероятности перехода в двоичном симметричном канале представлены следующим образом:
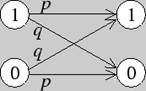
Рис. 2. Вероятности перехода в двоичном симметричном канале.
Для защиты передаваемых текстов от помех используются корректирующие коды, которые основаны на информационной избыточности. Самый простой способ создания избыточности достигается многократным дублированием передаваемых символов, т.е. образованием символьных блоков: 0→00000, 1→11111. В случае сбоя решение при дешифровке принимается по большинству оставшихся символов в блоке.
|
|
|
Существует очень простая, но эффективная защита информационного текста от единичного сбоя, которая требует минимальной избыточности в один дополнительный символ. Это проверка на четность. При кодировании к тексту добавляется 0 или 1 в зависимости от четности или нечетности суммы единиц в тексте. Если при декодировании обнаружится нечетное число единиц, значит, текст был принят неверно.
Процедура кодирования с помощью двух символов может быть представлена бинарным деревом. Длина ветвей, равная длине каждого кодового слова, определяет естественные порядковые уровни. Например, рассмотренный выше код Фано может быть представлен следующим бинарным деревом:

Рис. 3. Код Фано.
В нашем дереве символу 0 соответствует ребро, отклоняющееся влево, а символу 1 - ребро, отклоняющееся вправо.
Кодирование и декодирование используем для демонстрации передачи и хранения необходимой информации. Такой целостный взгляд на предложенную цепочку не только обогащает студента новыми знаниями, но и показывает целостность математики. Так, рассматриваемый материал дает представление, сколь широки и разнообразны связи теории кодирования и декодирования с разными разделами математики (алгебра, геометрия, комбинаторный анализ) и как порой абстрактные математические теории могут с успехом применяться для решения практических задач.
Двоичным (m,n) - кодом называется пара, состоящая из схемы кодирования Е: 2m→2n и схемы декодирования Д: 2n→2nm, где 2n - множество всех двоичных последовательностей длины n. Функции Е и D выбираются так, чтобы функция H=E*T*D (T - "функция ошибок") с вероятностью, близкой к единице, была тождественной.
Коды делятся на два класса. Коды с исправлением ошибок имеют целью правильно восстановить с вероятностью, близкой к единице, посланное сообщение. Коды с обнаружением ошибок имеют целью выявить с вероятностью, близкой к единице, наличие ошибок.
|
|
|
 Существуют две большие группы алгоритмов архивации: сжатие без потерь - биективно перекодирует информацию, то есть возможно абсолютно идентичное ее восстановление; сжатие с потерями необратимо удаляет из информации некоторые сведения, оказывающие наименьшее влияние на смысл сообщения.
Существуют две большие группы алгоритмов архивации: сжатие без потерь - биективно перекодирует информацию, то есть возможно абсолютно идентичное ее восстановление; сжатие с потерями необратимо удаляет из информации некоторые сведения, оказывающие наименьшее влияние на смысл сообщения.
Как Вам известно, подавляющее большинство современных форматов записи данных содержат их в виде, удобном для быстрого манипулирования, для удобного прочтения пользователями. При этом данные занимают объем больший, чем это действительно требуется для их хранения. Алгоритмы, которые устраняют избыточность записи данных, называются алгоритмами сжатия данных, или алгоритмами архивации. В настоящее время существует огромное множество программ для сжатия данных, основанных на нескольких основных способах.
Зачем же нужна архивация в криптографии? Дело в том, что в современном криптоанализе, то есть науке о противостоянии криптографии, с очевидностью доказано, что вероятность взлома криптосхемы при наличии корреляции между блоками входной информации значительно выше, чем при отсутствии таковой. А алгоритмы сжатия данных по определению и имеют своей основной задачей устранение избыточности, то есть корреляций между данными во входном тексте.
Все алгоритмы сжатия данных качественно делятся на 1) алгоритмы сжатия без потерь, при использовании которых данные на приемной восстанавливаются без малейших изменений, и 2) алгоритмы сжатия с потерями, которые удаляют из потока данных информацию, незначительно влияющую на суть данных, либо вообще невоспринимаемую человеком (такие алгоритмы сейчас разработаны только для аудио- и видео- изображений). В криптосистемах, естественно, используется только первая группа алгоритмов.
Существует два основных метода архивации без потерь:
- алгоритм Хаффмана (англ. Huffman), ориентированный на сжатие последовательностей байт, не связанных между собой,
- алгоритм Лемпеля-Зива (англ. Lempel, Ziv), ориентированный на сжатие любых видов текстов, то есть использующий факт неоднократного повторения "слов" – последовательностей байт.
Практически все популярные программы архивации без потерь (ARJ, RAR, ZIP и т.п.) используют объединение этих двух методов – алгоритм LZH.
Алгоритм Хаффмана
Алгоритм сжатия ориентирован на неосмысленные последовательности символов какого-либо алфавита. Необходимым условием для сжатия является различная вероятность появления этих символов (и чем различие в вероятности ощутимее, тем больше степень сжатия).
|
|
|
Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.
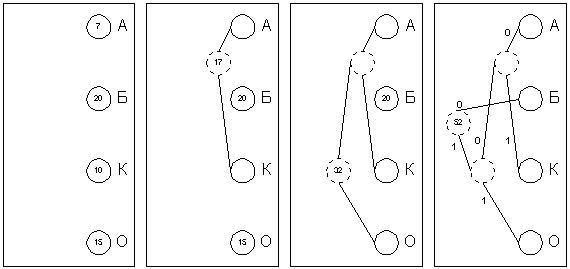
| а | б | в | г |
Рис. 4. Префиксный код Хаффмана.
Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии (то есть информационной насыщенности). Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа (рис. 4а). Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов (рис. 4б). Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом (рис. 4в и 4г). Для проверки: очевидно, что в ней будет записана длина кодируемого файла (текста). Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".
В теории кодирования информации показывается, что код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б": "01-00010100001", затем снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".
Работа алгоритма с файлами
Сначала кажется, что создание файла меньших размеров из исходного без кодировки последовательностей или исключения повтора байтов будет невозможной задачей. Но давайте мы заставим себя сделать несколько умственных усилий и понять алгоритм Хаффмана.
Сжимая файл по алгоритму Хаффмана первое что мы должны сделать - это необходимо прочитать файл полностью и подсчитать сколько раз встречается каждый символ из расширенного набора ASCII. Если мы будем учитывать все 256 символов, то для нас не будет разницы в сжатии текстового и EXE файла. После подсчета частоты вхождения каждого символа, необходимо просмотреть таблицу кодов ASCII и сформировать мнимую компоновку между кодами по убыванию. То есть не меняя местонахождение каждого символа из таблицы в памяти отсортировать таблицу ссылок на них по убыванию. Каждую ссылку из последней таблицы назовем "узлом". В дальнейшем (в дереве) мы будем позже размещать указатели которые будут указывает на этот "узел". Для ясности давайте рассмотрим пример:
Мы имеем файл длиной в 100 байт и имеющий 6 различных символов в себе. Мы подсчитали вхождение каждого из символов в файл и получили следующее:
┌─────────────────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ cимвол │ A │ B │ C │ D │ E │ F │
├─────────────────┼─────┼─────┼─────┼─────┼─────┼─────┤
│ число вхождений │ 10 │ 20 │ 30 │ 5 │ 25 │ 10 │
└─────────────────┴─────┴─────┴─────┴─────┴─────┴─────┘
Теперь мы берем эти числа и будем называть их частотой вхождения
для каждого символа. Разместим таблицу как ниже.
┌─────────────────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ cимвол │ C │ E │ B │ F │ A │ D │
├─────────────────┼─────┼─────┼─────┼─────┼─────┼─────┤
│ число вхождений │ 30 │ 25 │ 20 │ 10 │ 10 │ 5 │
└─────────────────┴─────┴─────┴─────┴─────┴─────┴─────┘
Мы возьмем из последней таблицы символы с наименьшей частотой. В нашем случае это D (5) и какой либо символ из F или A (10), можно взять любой из них например A.
Сформируем из "узлов" D и A новый "узел", частота вхождения для которого будет равна сумме частот D и A:
Частота 30 10 5 10 20 25
Символа C A D F B E
│ │
└──┬──┘
┌┴─┐
│15│ = 5 + 10
└──┘
Номер в рамке - сумма частот символов D и A. Теперь мы снова ищем два символа с самыми низкими частотами вхождения. Исключая из просмотра D и A и рассматривая вместо них новый "узел" с суммарной частотой вхождения. Самая низкая частота теперь у F и нового "узла". Снова сделаем операцию слияния узлов:
Частота 30 10 5 10 20 25
Символа C A D F B E
│ │ │
│ │ │
│ ┌──┐│ │
└─┤15├┘ │
└┬─┘ │
│ │
│ ┌──┐ │
└────┤25├─┘ = 10 + 15
└──┘
Рассматриваем таблицу снова для следующих двух символов (B и E). Мы продолжаем в этот режим пока все "дерево" не сформировано, т.е. пока все не сведется к одному узлу.
Частота 30 10 5 10 20 25
Символа C A D F B E
│ │ │ │ │ │
│ │ │ │ │ │
│ │ ┌──┐│ │ │ │
│ └─┤15├┘ │ │ │
│ └┬─┘ │ │ │
│ │ │ │ │
│ │ ┌──┐ │ │ ┌──┐ │
│ └────┤25├─┘ └─┤45├─┘
│ └┬─┘ └┬─┘
│ ┌──┐ │ │
└────┤55├──────┘ │
└─┬┘ │
│ ┌────────────┐ │
└───┤ Root (100) ├────┘
└────────────┘
Теперь когда наше дерево создано, мы можем кодировать файл. Мы должны всегда начинать из корня (Root). Кодируя первый символ (лист дерева С) Мы прослеживаем вверх по дереву все повороты ветвей и если мы делаем левый поворот, то запоминаем 0-й бит, и аналогично 1-й бит для правого поворота. Так для C, мы будем идти влево к 55 (и запомним 0), затем снова влево (0) к самому символу. Код Хаффмана для нашего символа C - 00. Для следующего символа (А) у нас получается - лево,право,лево,лево, что выливается в последовательность 0100. Выполнив выше сказанное для всех символов получим
C = 00 (2 бита)
A = 0100 (4 бита)
D = 0101 (4 бита)
F = 011 (3 бита)
B = 10 (2 бита)
E = 11 (2 бита)
Каждый символ изначально представлялся 8-ю битами (один байт), и так как мы уменьшили число битов необходимых для представления каждого символа, мы следовательно уменьшили размер выходного файла.
Сжатие складывается следующим образом:
┌──────────┬────────────────┬───────────────────┬──────────────┐
│ Частота │ первоначально │ уплотненные биты │ уменьшено на │
├──────────┼────────────────┼───────────────────┼──────────────┤
│ C 30 │ 30 x 8 = 240 │ 30 x 2 = 60 │ 180 │
│ A 10 │ 10 x 8 = 80 │ 10 x 3 = 30 │ 50 │
│ D 5 │ 5 x 8 = 40 │ 5 x 4 = 20 │ 20 │
│ F 10 │ 10 x 8 = 80 │ 10 x 4 = 40 │ 40 │
│ B 20 │ 20 x 8 = 160 │ 20 x 2 = 40 │ 120 │
│ E 25 │ 25 x 8 = 200 │ 25 x 2 = 50 │ 150 │
└──────────┴────────────────┴───────────────────┴──────────────┘
Первоначальный размер файла: 100 байт - 800 бит;
Размер сжатого файла: 30 байт - 240 бит;
240 - 30% из 800, так что мы сжали этот файл на 70%.
Все это довольно хорошо, но неприятность находится в том факте, что для восстановления первоначального файла, мы должны иметь декодирующее дерево, так как деревья будут различны для разных файлов. Следовательно мы должны сохранять дерево вместе с файлом. Это превращается в итоге в увеличение размеров выходного файла.
В нашей методике сжатия и каждом узле находятся 4 байта указателя, по этому, полная таблица для 256 байт будет приблизительно 1 Кбайт длинной.
Таблица в нашем примере имеет 5 узлов плюс 6 вершин (где и находятся наши символы), всего 11. 4 байта 11 раз - 44. Если мы добавим после небольшое количество байтов для сохранения места узла и некоторую другую статистику - наша таблица будет приблизительно 50 байтов длинны.
Добавив к 30 байтам сжатой информации, 50 байтов таблицы получаем, что общая длинна архивного файла вырастет до 80 байт. Учитывая, что первоначальная длинна файла в рассматриваемом примере была 100 байт - мы получили 20% сжатие информации.
Не плохо. То что мы действительно выполнили - трансляция символьного ASCII набора в наш новый набор требующий меньшее количество знаков по сравнению с стандартным.
Что мы можем получить на этом пути?
Рассмотрим максимум который мы можем получить для различных разрядных комбинаций в оптимальном дереве, которое является несимметричным.
Мы получим что можно иметь только:
4 - 2 разрядных кода;
8 - 3 разрядных кодов;
16 - 4 разрядных кодов;
32 - 5 разрядных кодов;
64 - 6 разрядных кодов;
128 - 7 разрядных кодов;
Необходимо еще два 8 разрядных кода.
4 - 2 разрядных кода;
8 - 3 разрядных кодов;
16 - 4 разрядных кодов;
32 - 5 разрядных кодов;
64 - 6 разрядных кодов;
128 - 7 разрядных кодов;
--------
Итак мы имеем итог из 256 различных комбинаций которыми можно кодировать байт. Из этих комбинаций лишь 2 по длинне равны 8 битам. Если мы сложим число битов которые это представляет, то в итоге получим 1554 бит или 195 байтов. Так в максимуме, мы сжали 256 байт к 195 или 33%, таким образом максимально идеализированный Huffman может достигать сжатия в 33% когда используется на уровне байта.
Все эти подсчеты производились для не префиксных кодов Хаффмана т.е. кодов, которые нельзя идентифицировать однозначно. Например код A - 01011 и код B - 0101. Если мы будем получать эти коды побитно, то получив биты 0101 мы не сможем сказать какой код мы получили A или B, так как следующий бит может быть как началом следующего кода, так и продолжением предыдущего.
Необходимо добавить, что ключем к построению префиксных кодов служит обычное бинарное дерево и если внимательно рассмотреть предыдущий пример с построением дерева можно убедится, что все получаемые коды там префиксные.
Одно последнее примечание - алгоритм Хаффмана требует читать входной файл дважды, один раз считая частоты вхождения символов, другой раз производя непосредственно кодирование.
Программная реализация алгоритма Huffman
Сразу хочу заметить, что описываемая ниже программная реализация алгоритма Huffman предназначается для сжатия файлов самого различного содержания и использует для каждого файла оптимальный вид бинарного дерева, т.е. один файл можно сжать используя несколько видов деревьев, но лишь одно из этих деревьев обеспечит для данного файла максимальное сжатие.
Например: строка "Business information systems"
Первое дерево: ("sp" - space)
s[6] i[3] n[3] t[2] o[2] e[2] sp[2] m[2] B[1] u[1] f[1] r[1] a[1] y[1]
│ │ │ │ │ │ │ │ │┌──┐│ │┌──┐│ │┌──┐│
│ │ │ │ │ │ │ │ 0└┤ 2├┘1 0└┤ 2├┘1 0└┤ 2├┘
│ 0│┌──┐│1 0│┌──┐│1 │ 0┌──┐1│ 0│┌───┐└─┬┘ └─┬┘ ┌───┐└─┬┘1
│ └┤ 6├┘ └┤ 4├┘ └──┤ 4├─┘ └┤ 4 ├──┘ └──┤ 4 ├──┘
│ └─┬┘ └─┬┘ └┬─┘ └─┬─┘1 0 └─┬─┘ 1
│0┌───┐1│ │ 0┌───┐1 │ │ 0┌────┐1 │
└─┤ 12├─┘ └──┤ 8 ├───┘ └──────┤ 8 ├───────┘
└─┬─┘ └─┬─┘ 0┌────┐1 └──┬─┘
│ └─────────┤ 16 ├────────────┘
│ 0┌──────────┐1 └──┬─┘
└───────────┤ Root ├────────┘
└──────────┘
Второе дерево:
s[6] i[3] n[3] t[2] o[2] e[2] sp[2] m[2] B[1] u[1] f[1] r[1] a[1] y[1]
│ │ │ │ │ │ │ │ │ │ │ │ │┌──┐│
│ │ │ │ │ 0│┌───┐1 │ ┌┘ └─┐ │ │ │ 0└┤ 2├┘1
│ │ │ │ │ └┤ 12├┐ │ 0│┌───┐1 │ │ │ 0│┌──┐ └─┬┘
│ │ │ │ 0│┌───┐└─┬─┘│ │ └┤ 8 ├┐ │ │ │ └┤ 3├───┘
│ │ │ │ └┤ 14├──┘ │ │┌──┐└─┬─┘│┌┘ │ 0│┌──┐1└─┬┘1
│ │ │ 0│┌───┐└─┬─┘1 │ └┤10├──┘ ││ │ └┤ 4├───┘
│ │ │ └┤ 16├──┘ │ 0└─┬┘1 ││ 0│┌──┐ └─┬┘
│ │ 0│┌───┐└─┬─┘1 └────┘ ││0 └┤ 5├───┘
│ │ └┤ 19├──┘ ││┌──┐└─┬┘1
│ 0 │┌───┐└─┬─┘1 │└┤ 6├──┘
│ └┤ 22├──┘ │ └─┬┘1
│ └─┬─┘1 └───┘
│ └───────────┐
│0┌─────────────┐1 │
└─┤ Root (28) ├───┘
└─────────────┘
Распишем коды полученные по различным деревьям:
по первому: по второму:
s[6] - 00 - 6*2=12 s[6] - 0 - 6*1 =6
i[3] - 010 - 3*3= 9 i[3] - 10 - 3*2 =6
n[3] - 011 - 3*3= 9 n[3] - 110 - 3*3 =9
t[2] - 1000 - 2*4= 8 t[2] - 1110 - 2*4 =8
o[2] - 1001 - 2*4= 8 o[2] - 11110 - 2*5 =10
e[2] - 1010 - 2*4= 8 e[2] - 111110 - 2*6 =12
sp[2] - 1011 - 2*4= 8 sp[2] - 1111110 - 2*7 =14
m[2] - 1100 - 2*4= 8 m[2] - 11111110 - 2*8 =16
B[1] - 11010 - 1*5= 5 B[1] - 111111110 - 1*9 =9
u[1] - 11011 - 1*5= 5 u[1] - 1111111110 - 1*10=10
f[1] - 11100 - 1*5= 5 f[1] - 11111111110 - 1*11=11
r[1] - 11101 - 1*5= 5 r[1] - 111111111110 - 1*12=12
a[1] - 11110 - 1*5= 5 a[1] - 1111111111110 - 1*13=13
y[1] - 11111 - 1*5= 5 y[1] - 1111111111111 - 1*13=14
─────────────────────── ────────────────────────────────
всего бит 100 байт 13 всего бит 150 байт 19
Из первоначальных 304 бит в первом случае осталось всего 100 бит, а во втором 150 бит. Из этого можно сделать вывод, что первое дерево является оптимальным (оно строится именно по алгоритму Huffman). Но не во всех приложениях возможно применение алгоритма построения дерева, поэтому нельзя сбрасывать со счета и использования "усредненного" дерева для многих, близких по статистической таблице, блоков данных.
В нашем случае мы строим для каждого отдельного файла свое дерево.
|
|
|


