Выражение (2.27) можно записать в виде 12 глава

Заметим, что предельное давление (5.52) не зависит от собственного веса грунта, хотя мы рассматривали весомую среду. С физической точки зрения это можно объяснить отсутствием внутреннего трения.

В общем случае весомого сыпучего основания, когда в замкнутом виде решения получить не удается. Здесь прибегают к численному интегрированию канонической системы уравнений статики сыпучей среды (5.16) по краевым задачам (см. п. 7.1). Впервые эту задачу для случая одностороннего выпора грунта решил В.В. Соколовский, а наиболее общее и важное с практической точки зрения решение для двухстороннего выпора было дано М.В. Малышевым и Ю.И. Соловьевым, которое мы и рассмотрим.

Расчетная схема задачи дана на рис. 5.10. Аналогично рассмотренным частным случаям здесь можно выделить зону максимального напряженного состояния OAB, область радиального веера OBC, зону под штампом O ¢ OC. Обратим внимание, что характеристики представлены прямыми только в зоне OAB, в остальных областях они криволинейны, т.е. и в OBC, и в O ¢ OC полученные ранее замкнутые решения не применимы. Для построения решения в этих зонах будем вынуждены обратиться к понятиям краевых задач, техника решения которых подробно рассмотрена в п. 7.1. Здесь же проследим основной ход построения поля напряжений, делая необходимые ссылки на указанный параграф.

 

Рисунок 5.10. - Сетка линий скольжения в задаче Прандтля для общего случая весомого сыпучего основания и эпюры предельных нормальных и касательных напряжений

по подошве штампа

 

Итак, предельное равновесие в зоне OAB определяется согласно (5.24), тогда на границе OB параметры канонической системы уравнений (5.16) равны

,

(5.53)

Зона OBC аналогична областям радиального веера, рассмотренным нами ранее, однако здесь, как уже указывалось, выполняется численное интегрирование канонической системы уравнений (5.16). В результате определяем характеристику OC.

После нахождения характеристики OC можно поступить двояко. Во-первых, можно рассмотреть равновесие части основания ABCC ¢, учитывая, что на CC ¢ в силу симметрии касательные напряжения отсутствуют, а на линии скольжения ABC определены все напряжения. В этом случае получим вертикальную равнодействующую предельного давления. Во-вторых, можно численно решить уравнения (5.16) при известных на характеристике OC и условиях на оси симметрии CC ¢:

(5.54)

Оказалось, что полученный таким путем результат можно привести к виду, аналогичному (5.47):

,

(5.55)

где N _g, N_q, N_c - коэффициенты несущей способности, причем значения N_q, N_c, получаемые в численных решениях, с большой точностью совпадают с рассчитанными по формулам (5.48).

Коэффициент также зависит только от угла внутреннего трения j. Коэффициент определяется только в численных решениях, на основании которых составлены соответствующие таблицы. Приведем несколько его значений (табл. 5.2).

 

Таблица 5.2 - Значения коэффициента

j	5°	10°	15°	20°	25°	30°	35°	40°	45°
N g	0,20	0,6	1,35	2,88	5,87	12,39	27,50	66,01	177,61

 

Из приведенных данных видно, что на значение коэффициента , также как и на , существенное влияет величина угла внутреннего трения j.

Для удобства практического использования результатов полученного решения при работе на ЭВМ можно предложить какую-либо аппроксимационную зависимость, например,

.

Данная формула в сочетании с (5.48) и (5.57) позволяет определять предельное давление на основание в общем случае весомого сыпучего грунта для вертикально приложенной нагрузки и с учетом трения по подошве фундамента (штампа).

Обращает на себя внимание тот факт, что если в случаях невесомого и идеально-связного основания эпюра предельных нормальных напряжений по подошве была равномерной, а касательные напряжения отсутствовали, то в общем случае эпюра нормальных напряжений имеет выпуклую форму с максимальным значением под серединой штампа (фундамента), и, кроме того, появляются касательные напряжения. Это означает наличие трения по подошве штампа, который в этом случае называют шероховатым. Таким образом, формула (5.55) определяет среднее значение предельного давления по подошве.

Можно решить аналогичную задачу с несколько иной последовательностью краевых задач, потребовав отсутствие трения по подошве штампа, который в этом случае будет называться гладким. Такое решение, как уже отмечалось, было получено и подробно проанализировано В.В. Соколовским. В рассмотренном нами случае жесткого штампа имеет место двухсторонний выпор грунта, как говорят, по схеме Прандтля, при гладком штампе - односторонний выпор по схеме Хилла. При этом по схеме Хилла среднее предельное давление по подошве окажется меньше, чем по схеме Прандтля. Для частных случаев невесомого и идеально-связного оснований предельное давление по обеим схемам совпадает.

Отметим, что формула (5.55) используется в нормах проектирования для расчета несущей способности оснований.

В заключение коснемся случая весомого идеально-сыпучего основания. Очевидно, что при определении предельного давления по формуле (5.55) нужно принять . Для непригруженного () идеально сыпучего основания (5.55) примет вид

.

(5.56)

Данный предельный переход подтверждает гипотезу, выдвинутую еще Н.М. Герсевановым, о том, что при одинаковых граничных условиях предельное состояние весомого сыпучего грунта суммируется из двух частных случаев - невесомого сыпучего и весомого идеально-сыпучего.

 

5.2.6. О построении осесимметричных решений

 

В осесимметричных задачах теории предельного равновесия грунтов ось симметрии принимается совпадающей с направлением силы тяжести, т.е. вертикальной. Осесимметричное напряженное состояние рассматривается в цилиндрической системе координат . На рис. 5.11 в системе координат показаны положительные направления напряжений , действующих по площадкам элементарного объема грунта, выделенного двумя бесконечно близкими плоскостями, проходящими через вертикальную ось , двумя цилиндрическими поверхностями и двумя горизонтальными плоскостями. Единственная объемная сила - удельный вес грунта - действует вертикально вниз.

 

 

 

Рисунок 5.11. - Напряженное осесимметричное состояние

 

Дифференциальные уравнения равновесия в цилиндрической системе координат при осесимметричном напряженном состоянии имеют вид:

, .

(5.57)   (5.58)

Система двух уравнений (5.57)…(5.58) содержит четыре неизвестные функции напряжений s _z, s _r, s_q и t _rz от координат . Для замыкания этой системы необходимы еще два дополнительных условия.

В качестве первого дополнительного условия в теории предельного равновесия грунтов принимается условие прочности Кулона-Мора:

.

(5.59)

В качестве второго условия принимается равенство главного напряжения s_q наибольшему или наименьшему главному напряжению:

или .

(5.60)

Причем s_q = s₃ при деформациях в основании, направленных от оси симметрии, а s_q = s₁ при деформациях, направленных к оси симметрии. Условность такого подхода заключается в том, что в статическом методе ТПРГ деформации не рассматриваются (см. п.4.2.2). Однако в большинстве работ по осесимметричному предельному напряженному состоянию придерживаются данной гипотезы.

Равенства (5.60) еще называют концепцией полной плстичности или гипотезой полной плстичности.

Аналитических решений для осесимметричного напряженного состояния в основании получено не было. Для выполнения численных решений методом конечных разностей система уравнений (5.57)…(5.60) преобразуется к системе дифференциальных уравнений, справедливых вдоль линий скольжения, т.е. к каноническому виду. Обозначим через угол - наклон первого главного напряжения к оси , а величиной - приведенное среднее напряжение.

Тогда напряжения s _z, s _r, s_q и t _rz можно определить формулами:

, , ; при sq = s3, при sq = s1.

(5.61)

Подставляя выражения (5.61) в уравнения равновесия (5.57)…(5.58) и выполнив необходимые преобразования аналогично описанным в п. 5.2.3, получаем каноническую систему уравнений осесимметричной задачи статики сыпучей среды, записанную по характеристикам:

, , , ,

(5.62)

где .

Эта система впервые была получена В.Г. Березанцевым. Верхние знаки в уравнениях (5.62) соответствуют деформациям основания, направленным от оси, а нижние - деформациям, направленным к оси.

В качестве примера на рис. 5.12 приведены результаты построения сетки линий скольжения и определения предельного давления в основании под цилиндрическим круговым фундаментом по В.Г. Березанцеву. Это решение содержит следующее упрощение - очертание линий скольжения получено не прямым интегрированием канонической системы уравнений (5.62), а взято из решения плоской задачи для невесомой среды.

 

 

Рисунок 5.12. - Сетка линий скольжения в осесимметричной задаче Прандтля

по В.Г. Березанцеву

 

Предельная нагрузка дается аналогичной (5.55) формулой

,

где N _g, N_q, N_c - коэффициенты несущей способности круглого штампа (табл. 5.3), r - радиус штампа.

 

Таблица 5.3. - Коэффициенты несущей способности круглого штампа (по В.Г. Березанцеву)

j	5°	10°	15°	20°	25°	30°	35°	40°	45°
N g	0,725	1,694	3,564	7,385	15,63	34,64	82,45	216,5
Nq	1,428	2,493	4,469	8,308	16,19	33,56	75,32	187,5	535,7
Nc	6,797	9,411	13,57	20,54	32,94	56,69	106,4	222,5	5,348

 

Надо сказать, что при построении осесимметричных решений приходится сталкиваться с наибольшим количеством трудностей. Во-первых, как уже отмечалось, это - отсутствие аналитических решений даже в простейших случаях. Во-вторых, в рамках концепции полной пластичности удается получить решения для ограниченного диапазона граничных условий. Это вызвано тем, что уже в первой краевой задаче линии скольжения обладают существенной кривизной. В-третьих, сравнивая (5.60) и (5.62) можно убедиться, что на оси симметрии правые части третьего и четвертого уравнений (5.62) обращаются в неопределенности типа .

В заключение отметим, что некоторые приближенные решения осесимметричных задач ТПРГ используются в нормах проектирования при определении расчетного сопротивление грунта под нижним концом буронабивной сваи.

5.3 Устойчивость откосов и склонов

 

5.3.1. Предельная высота вертикального откоса

 

Рассмотрение проблемы устойчивости откосов и склонов начнем с наиболее простой задачи определения предельной высоты вертикального откоса. В строительстве, особенно при производстве работ, этот вопрос имеет самостоятельное значение.

Из практического опыта известно, что грунт в состоянии держать весьма крутые и даже вертикальные откосы. Однако также понятно, что высота такого откоса не может быть бесконечно большой - она зависит от прочности грунта и внешнего давления на бровке откоса.

Рассмотрим схему, показанную на рис. 5.13. Грунт характеризуется параметрами прочности j и c, удельным весом g. Для общности предположим, что на бровке действует нагрузка интенсивностью p. Предельную высоту вертикального откоса обозначим через h _пр. Таким образом, откос находится в предельном напряженном состоянии. Поскольку граница откоса принимается свободной, то напряжения s _z и s _x на ней - главные, причем в нижней точке откоса

 

 

Рисунок 5.13. - К определению предельной высоты вертикального откоса

 

 

.

(5.63)

Подставим напряжения (5.63) в условие прочности Кулона-Мора в главных напряжениях:

,

(5.64)

Тогда для свободного от внешней нагрузки вертикального откоса его предельная высота определится как

(5.65)

 

5.3.2. Предельное давление на невесомый откос

 

Прежде чем переходить к более общим случаям, рассмотрим задачу о предельном давлении на невесомый откос в рамках строгого метода ТПРГ. На практике такая идеализация может быть допустима, если собственный вес откоса считать незначительным по сравнению с ожидаемой на него нагрузкой.

Область предельного напряженного состояния ОАВСD, представленная на рис. 5.14, состоит из области максимального ОАВ, переходного ОВС и минимального ОСD напряженных состояний грунта. На свободной поверхности откоса ОА 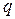= 0. Поэтому здесь можно считать действующей приведенную пригрузку , и напряженное состояние в области ОAВ определится формулами (5.21) при = 0, если заменить s _x и s _z на s₁ и s₃ соответственно. В частности, согласно (5.22) приведенное среднее напряжение

 

 

Рисунок 5.14. - Схема к определению предельного давления на невесомый откос

 

.

(5.66)

Граница ОВ составляет с осью Oz угол

,

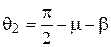(5.67)

где b - угол наклона откоса к оси Oх.

Заметим, что в области ОAВ .

Как и в задаче о предельном давлении на невесомое горизонтальное основание, в зоне ОВС согласно (5.31)

.

(5.68)

Произвольную постоянную s₀ определим, приравняв (5.68) к (5.66) при :

.

Отсюда

(5.69)

В результате полностью определяются напряжения и в области ОВС. При этом вдоль границы ОС согласно (5.68) при с учетом (5.69) имеем

.

(5.70)

Наконец, приравнивая (5.70) к (5.22) при = 0 и p = p_u

,

определим предельное давление на откос:

.

(5.71)

Полагая в (5.71) , имеем формулу Прандтля (5.46) для случая горизонтального основания при .

 

5.3.3. Равноустойчивый контур откоса

 

В предыдущем пункте мы рассмотрели задачу о предельном давлении на откос в предположении о невесомости грунта. На практике наряду с внешней нагрузкой собственный вес является существенным фактором, способствующим обрушению склонов. Поскольку решения, приводимые в настоящем пункте являются строгими решениями ТПРГ, грунт, как и ранее, принимается однородным и изотропным.

Рассмотрим вначале задачу о равноустойчивом очертании естественного откоса. Расчетная схема показана на рис. 5.15, а. Как следует из п. 5.3.1, грунт может держать вертикальный откос, максимальная высота которого h _пр рассчитывается по формуле (5.65). Очевидно, что если высота откоса будет меньшей, то предельное состояние в нем не достигается. Следовательно, чтобы склон находился в предельном состоянии необходимо на границе OD приложить давление p, равное бытовому давлению от веса слоя грунта мощностью h _пр.

 

Рисунок 5.15. - Схемы определению контура равноустойчивого склона: (а) - при давлении сверху, равному бытовому от предельной высоты вертикального откоса, (б) - при давлении большем, чем бытовое от предельной высоты вертикального откоса

.

(5.72)

Теперь в откосе можно выделить две зоны - зона минимального напряженного состояния OCD и приоткосный участок ACO. В зоне OCD согласно (5.22) имеют место равенства:

.

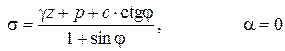(5.73)

В приоткосном участке ACO приходим к необходимости численной реализации канонической системы уравнений (5.16). Принципы этого решения изложены ниже в п.7.1.3. Особенность данного решения заключается в том, что очертание контура заранее неизвестно, оно определится лишь в результате решения.

На рис. 5.16 даны схемы равноустойчивых контуров для весомой идеально-сыпучей среды (а), весомой идеально-связной среды (б) и общего случая сыпучей среды (в). Из рисунка видно, что случаи идеально-сыпучего и идеально-связного грунта являются предельными для общего случая.

Рассмотрим построение равноустойчивого склона, если на бровке действует нагрузка (рис. 5.15, б)

.

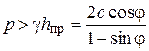Рисунок 5.16. - Очертание равноустойчивых откосов для случаев (а) - идеально-сыпучего грунта, (б) - идеально-связного грунта, (в) - весомого сыпучего грунта

Здесь выделяют три зоны: зона минимального напряженного состояния OCD, приоткосный участок ACB и переходная область OCB. Таким образом, компоновка краевых задач совпадает с рассмотренной в п. 5.3.2 с тем отличием, что в невесомом откосе решение строилось с границы AO к границе OD, а в нашем случае наоборот - с OD к OA. В остальном схема численного решения та же.

На рис. 5.17 показаны различные очертания равноустойчивого контура при различных давлениях p на бровке.

 

Рисунок 5.17. - Очертание равноустойчивого склона при различном давлении на бровке

 

 

5.3.4. Расчет устойчивости откосов и склонов методами отсеков

 

Перейдем к рассмотрению наиболее общего случая определения устойчивости откосов и склонов, когда очертание склона и геологическое строение может быть произвольным, а положение и величина нагрузок, действующих на склон, заданы. Как уже отмечалось, при столь общих предположениях строгих решений ТПРГ получить не удается. Поэтому здесь прибегают к приближенным методам расчета, так называемым, «методам отсеков».

Напомним принципиальную суть этих методов (п. 3.1.2) на примере плоской задачи. В заданном склоне, устойчивость которого требуется определить, проводят некоторую поверхность скольжения, выделяя, таким образом, область обрушения грунта. Далее эту область условно разбивают на отсеки, для каждого из которых рассматривают систему действующих на него сил. Рассмотрев равновесие всего массива в целом или только сил, действующих на выбранной поверхности скольжения, делают вывод об общей устойчивости склона. При этом в процессе расчета требуется определить наиболее опасную линию скольжения, форма и положение которой также заранее неизвестны. Поэтому приходится выполнять несколько расчетов с разными поверхностями скольжения.

Рассмотрим последовательность вычислений. Пусть дан склон, очертание и геологическое строение которого показано на рис. 5.18. Зададимся некоторой поверхностью скольжения, форму и положение которой в первом приближении можно назначить, например, исходя из характера напластования слоев, или общих соображений о характере возможного обрушения склона. Поскольку решается плоская задача, будем поверхность скольжения иногда называть линией скольжения.

Рисунок 5.18. - Схема у расчету устойчивости произвольного склона

 

Вертикальными линиями выделенную область обрушения разобьем на n отсеков. Рассмотрим систему сил, действующих на произвольный i -ый отсек (рис. 5.19). Здесь придется сделать несколько допущений, без которых расчет существенно усложняется.

Для простоты предположим, что верхняя грань отсека свободна от нагрузки, которую, как будет показано ниже, при необходимости нетрудно учесть. По боковым граням действуют силы взаимодействия с соседними отсеками F_i ¢ и F_i ¢¢. В простейшем варианте методов отсеков принимают, что эти силы взаимно уравновешены.

Далее определим собственный вес отсека

, (5.74)

где g _i - средневзвешенный удельный вес грунтов, попадающих в i -ый отсек; A_i - площадь отсека, численно равная его объему, так как имеет место плоская задача.

 

Рисунок 5.19. - Система сил, действующих на i -ый отсек

Силу собственного веса приложим в центре подошвы отсека и разложим на нормальную и касательную составляющие к подошве

, , (5.75)

где a _i - угол наклона подошвы к горизонту.

Касательная составляющая Q_i, как видно из рис. 5.19, будет стремиться сдвинуть отсек по линии скольжения. Этому препятствует сила трения T_i, возникающая по подошве, которую определим по закону Кулона в зависимости от нормальной составляющей N_i.

Таким образом, собственный вес каждого отсека с одной стороны способствует его смещению вниз по поверхности скольжения, а с другой - прижимает к несмещающимся породам, определяя величину удерживающей силы трения.

Чтобы перейти от напряжений, фигурирующих в законе Кулона, к силам умножим обе части (3.9) на площадь подошвы отсека l_i ´1, по которой и действуют рассматриваемые силы:

.

, (5.76)

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: