6.5.1 Сравнительная оценка коэффициентов регулятора положения для малого и средних перемещений

6. 5. 1 Сравнительная оценка коэффициентов регулятора положения для малого и средних перемещений

 

Для режима малых перемещений (РМП) при настройке контуров тока, скорости и положения на модульный оптимум

Т_с = 2Т_т, Т_т = 2Т_m, Т_m = 0, 005с.

Пусть максимальный момент равен М_м^*=2 и Т_м^/=1с, тогда численное значение коэффициента регулятора положения будет равно

К_рп* = 1/2Т_с = 1/8 Т_m = .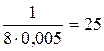

Для режима средних перемещений

К_рп^* = 2М_м^*/Т_м^/= .

Таким образом, контур положения, оптимизированный для режима малых перемещений, имеет коэффициент значительно больший, чем настроечное значение коэффициента для режима средних перемещений, поэтому отработка заданий будет, как правило, осуществляться с перерегулированием.

 

6. 6 Режим больших перемещений

 

К большим перемещениям относят перемещения больше настроечного q^*_з> q^*_{з(настр)}.

Рисунок 6. 14                                        Рисунок 6. 15

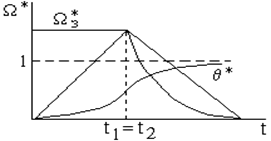
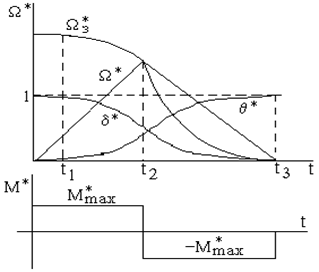
Тахограмма отработки больших перемещений показана на рисунке 6. 14. Так как в этом случае торможение начинается при максимальной скорости, равной единице в относительных единицах, поэтому коэффициент регулятора должен быть таким же, как и для настроечного перемещения. Поэтому все перемещения будут происходить оптимально (см. рисунок 6. 15).

 

6. 7 Применение параболического регулятора положения

 

Для того чтобы перемещения меньше настроечного, отрабатывались оптимально, регулятор положения должен быть нелинейным. Для подтверждения проанализируем отработку перемещения, меньшего настроечного, которое будет оптимальным (см. рисунок 6. 16).

Рисунок 6. 16

 

К_рп^*=2 .

В момент времени t £ t₁ U_рп^*= 1; в момент времени t > t₁ U_рп^*= К_рп^* (q^*_з – q^*).

Тогда U_рп^*= ,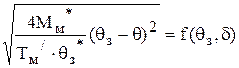

где d = q^*_з – q^*.

В момент времени t = t₂: d₍₂₎ = q^*_з/2.

Тогда U_рп^* = .

Если выходной сигнал регулятора в каждой точке является функцией ошибки, то и в точке, соответствующей моменту времени t₂ выходной сигнал будет также являться функцией этой ошибки. Для этого выходной сигнал должен быть равен

U_рп^* = .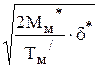

Такую статическую характеристику имеет параболический регулятор (рисунок 6. 17).

Рисунок 6. 17                                                 Рисунок 6. 18

 

Найдем коэффициент параболического регулятора

К_рп^*= .

При d^*®¥ К_рп^*®0; при d^*®0 К_рп^*®¥.

Осциллограмма сигналов при отработке заданных перемещений позиционной системой с параболическим регулятором представлена на рисунке 6. 18.

U_рп^*_(нач) = К_рп^*× q_з^* = ;

q^*_З(МАКС) = .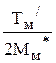

Сравнивая с настроечным перемещение q^*_З(МАКС) можно сделать вывод, что оптимальность отработки сигналов с параболическим регулятором положения возможно в диапазоне перемещений, вдвое меньше настроечных q^*_З(МАКС) = q^*_{З(настр)}/2.

В момент времени t₂ U_рп^* = .

Рисунок 6. 20                                                          Рисунок 6. 21

Для общего случая практическая реализация параболического регулятора положения (ПРП) имеет вид, представленный на рисунке 6. 19. При практической реализации начальный угол должен быть ограничен коэффициентом, который имеет контур положения в режиме малых перемещений. Реализация такой нелинейной зависимости осуществляется методом кусочно-линейной аппроксимации (рисунок 6. 20).

Рисунок 6. 19

 

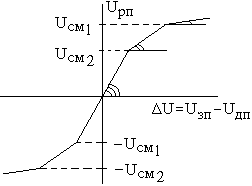
В соответствии с рисунком 6. 21, при реализации ПРП используется принцип смещенных диодов, который включается при достижении сигнала с выхода определенного уровня, и включает параллельно основному резистору R₀ резистор R₀₁, либо еще R₀₂.

ПРП позволяет адаптировать (приспособить) позиционную систему, делая оптимальными процессы отработки задающих сигналов, меньших максимального значения.

К₀ = R₀/R_дп; К₁ = ; .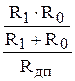

⇐ Предыдущая32333435363738394041Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: