Основные определения и аксиомы

Обоснование выбора решения в предыдущих главах выпол­нялось с позиции объективиста. Если же ЛПР - субъективист, то он будет руководствоваться индивидуально определенным БДЭ. Поясним смысл этой величины. Рассмотрим ситуацию, когда игрок с вероятностью 0,8 выигрывает 40 дол. и с вероятностью 0,2 проигрывает 20 дол. Попробуем выяснить, за какую сумму ЛПР уступит свое право участвовать в игре. Как отмечалось, объективист пользуется правилом: БДЭ = ОДО = 0,8*40 + 0,2 (–20) = 28 дол. Поэтому свое право на игру он уступит не менее чем за 28 дол. Субъективист, как правило, готов уступить свое право на игру за меньшую сумму, поскольку для него БДЭ < ОДО. Причинами такого поведения могут быть:

• финансовое состояние игрока (возможно, он на грани бан­кротства и ему необходимы денежные средства);

• отношение игрока к риску вообще (склонность к риску);

• настроение или состояние здоровья игрока;

• множество других, даже непосредственно не относящихся к бизнесу причин.

Величина БДЭ может изменяться со временем в зависимости от обусловленных указанными причинами обстоятельств. Например, в случае катастрофической нехватки финансовых средств (наличных денег) право на игру можно уступить и за более низкий эквивалент.

Исследуем реалистичность критерия выбора решения, осно­ванного на расчете ОДО. Рассмотрим две альтернативы:

1) выигрыш 1 000 000 дол. с вероятностью 1;

2) игра (лотерея): выигрыш 2 100 000 дол. с вероятностью 0,5 и проигрыш 50 000 дол. с вероятностью 0,5. В этом случае

ОДО= 0,5* 2 100 000 - 0,5* 50 000 = 1 025 000 дол.

Относительно получаемого среднего выигрыша указанные альтернативы практически эквивалентны, и если игрок безраз­личен к риску, он выберет вторую альтернативу. Если он к риску не безразличен, а подавляющее число людей именно таковыми являются, то выбор будет зависеть главным образом от финансо­вого состояния игрока. Игроки, имеющие скромный денежный доход, предпочтут не рисковать и выберут гарантированный выигрыш. Для ЛПР, обладающего достаточно крупным капита­лом, проигрыш в 50 000 дол. невелик, и он предпочтет рискнуть. Рисковать будут также игроки, патологически склонные к фи­нансовым авантюрам.

В данной главе будут изложены основы математической те­ории принятия субъективных решений [13]. Методология раци­онального принятия решений в условиях неопределенности, основанная на функции полезности индивида, опирается на пять аксиом, которые отражают минимальный набор необходимых условий непротиворечивого и рационального поведения игрока. Для компактного изложения аксиом нам потребуется следующее определение.

Определение 4.1. Предположим, что конструируется игра, в которой индивид с вероятностью а получает денежную сумму х и с вероятностью (1 – a) - сумму z. Эту ситуацию будем обозна­чать G(x, z: a).

Аксиома 1. Аксиома сравнимости (полноты). Для всего мно­жества S неопределенных альтернатив (возможных исходов) индивид может сказать, что либо исход х предпочтительнее ис­хода у (х у), либо у х, либо индивид безразличен в отноше­нии к выбору между х и у (х у). Запись х у означает, что исход х предпочтительнее исхода у либо индивид безразличен в отношении к выбору между х и у.

Аксиома 2. Аксиома транзитивности (состоятельности). Если х у и у z, то х z. Если х у и у z, то х z.

Аксиома 3. Аксиома сильной независимости. Предположим, что мы конструируем игру, в которой индивид с вероятностью а получает денежную сумму х и с вероятностью (1 - α) — сумму z, т.е. G(x, z: α). Сильная независимость означает, что если ин­дивид безразличен в отношении к выбору между х и у (х у),то он также будет безразличен в отношении к выбору между игрой (лотереей) G (x, z: α) и игрой G (y, z: α), т.е. из х у следует G (x, z: α) G (y, z: α).

Аксиома 4. Аксиома измеримости. Если х у z или х у z, то существует единственная вероятность α, такая, что у G (x, z: α).

Поясним смысл этой аксиомы. Пусть, например, имеем три исхода: х = 1000; у = 0; z означает смерть игрока. Исходя из здра­вого смысла смерть нельзя сравнивать ни с каким выигрышем, и соответствующего этому исходу значения вероятности α суще­ствовать не может. Однако в жизни бывают ситуации, когда некий проигрыш равнозначен смерти. Тогда утверждение у G (x, z: α) можно считать справедливым для некоторого значения .

Аксиома 5. Аксиома ранжирования. Если альтернативы у и и находятся по предпочтительности между альтернативами х и z и можно построить игры, такие, что индивид безразличен в отно­шении к выбору между у и G (x, z: α₂), a также к выбору между и и G(x, z: α₂), то при у и.

Поясним смысл этой аксиомы. Пусть существуют следующие альтернативы: х = 1000; у = 500; и = 200; z = –10. Пусть эквива­лентны две пары ситуаций, одна из которых неигровая, а другая игровая:

1) гарантированно получить 500 или игра: с вероятностью α₁, выиграть 1000 и с вероятностью (1 – α₁) проиграть 10, т.е.

500 G (1000, -10: α₁);

2) гарантированно получить 200 или игра: с вероятностью α₂ выиграть 1000 и с вероятностью (l - α₂) проиграть 10, т.е.

200 G (1000, -10: α₂).

Очевидно, что при указанных условиях α₁ α₂. Если α₁ + α₂, то у и.

Утверждение аксиомы вполне соответствует здравому смыс­лу: чем больше вероятность крупного выигрыша, тем больше игра «стоит», т.е. тем большая плата потребуется за приобретение права участвовать в этой игре.

Если принять приведенные аксиомы и предположить, что люди предпочитают большее количество некоторого блага мень­шему, то все это в совокупности определяет рациональное пове­дение ЛПР.

При названных предположениях американскими учеными Дж. Нейманом и О. Моргенштерном было показано, что ЛПР при принятии решения будет стремиться к максимизации ожи­даемой полезности. Другими словами, из всех возможных реше­нии он выберет то, которое обеспечивает наибольшую ожидае­мую полезность. Сформулируем определение полезности по Нейману-Моргенштерну.

Определение 4.2. Полезность - это некоторое число, припи­сываемое лицом, принимающим решение, каждому возможному исходу. Функция полезности Неймана - Моргенштерна для ЛПР показывает полезность, которую он приписывает каждому воз­можному исходу. У каждого ЛПР своя функция полезности, ко­торая показывает его предпочтение к тем или иным исходам в зависимости от его отношения к риску.

Определение 4.3. Ожидаемая полезность события равна сум­ме произведений вероятностей исходов на значения полезностей этих исходов.

Проиллюстрируем практическую реализацию введенных по­нятий на примере расчета ОДО и сопоставления этого значения с полезностью.

Задача 4.1. Нефтеперерабатывающая фирма решает вопрос о бурении скважины. Известно, что если фирма будет бурить, то с вероятностью 0,6 нефти найдено не будет; с вероятностью 0,1 запасы месторождения составят 50 000 т; с вероятностью 0,15 -100 000 т; с вероятностью 0,1 - 500 000 т; с вероятностью 0,05 -1 000 000 т. Если нефть не будет найдена, то фирма потеряет 50 000 дол.; если мощность месторождения составит 50 000 т, то потери снизятся до 20 000 дол.; мощность месторождения в 100 000 т принесет прибыль 30 000 дол.; 500 000 т- 430 000 дол.; 1 000 000 т - 930 000 дол. Дерево решений данной задачи пред­ставлено на рис. 4.1. Нетрудно рассчитать ожидаемое значение вы­игрыша:

ОДО = 0,6(-50 000) + 0,1 (-20 000) + 0,15*30 000 + + 0,1*430 000 + 0,05*930 000 = 62 000 дол.

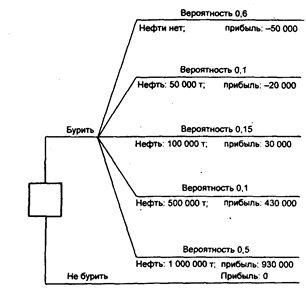
Рис. 4.1. Дерево решений для задачи 4.1 (прибыль указана в долларах)

 

Если ЛПР, представляющий фирму, безразличен к риску и принимает решение о проведении буровых работ на основании рассчитанного ОДО, то он воспринимает ожидаемую полезность как пропорциональную ОДО, полагая U = 62. Учитывая, что U - индивидуальное число, характеризующее ЛПР, нули, отвечаю­щие расчету ОДО, можно отбросить. В этом случае функция полезности U(v), где v - прибыль, получаемая при различных исходах, является прямой с положительным наклоном. Ниже бу­дет показано, что U можно задавать с точностью до некоторого монотонного преобразования.

Для принятия решения в случае небезразличия ЛПР к риску необходимо уметь оценивать значения полезности каждого из допустимых исходов. Дж. Нейман и О. Моргенштерн предложи­ли процедуру построения индивидуальной функции полезности, которая (процедура) заключается в следующем: ЛПР отвечает на ряд вопросов, обнаруживая при этом свои индивидуальные предпочтения, учитывающие его отношение к риску. Значения полезностей могут быть найдены за два шага.

Шаг 1. Присваиваются произвольные значения полезностей выигрышам для худшего и лучшего исходов, причем первой величине (худший исход) ставится в соответствие меньшее чис­ло. Например, для приведенной выше задачи U (-50 000 дол.) = 0, а U (930 000 дол.) = 50. Тогда полезности промежуточных выиг­рышей будут находиться в интервале от 0 до 50. Полезность исхода даже для одного индивида определяется не однозначно, а с точностью до монотонного преобразования. Пусть, напри­мер, имеем x₁, х₂,..., х_n - полезности, приписываемые п ожида­емым значениям выигрышей. Тогда α+β x₁, α + β х₂,..., α + β х_n (где (β > 0) также будут полезностями. Если в задаче 4.1 при рас­чете полезности отбросить последние нули, это будет эквивален­тно линейному преобразованию функции полезности при α = 0и β = 0,001.

Шaг 2. Игроку предлагается на выбор: получить некоторую гарантированную денежную сумму , находящуюся между луч­шим и худшим значениями S и s, либо принять участие в игре, т.е. получить с вероятностью р наибольшую денежную сумму S и с вероятностью (1 - р) - наименьшую сумму s. При этом ве­роятность следует изменять (понижать или повышать) до тех пор, пока ЛПР станет безразличным в отношении к выбору между получением гарантированной суммы и игрой. Пусть указанное значение вероятности равно р₀. Тогда полезность гарантирован­ной суммы определяется как среднее значение (математическое ожидание) полезностей наименьшей и наибольшей сумм, т.е.

U ( ) = p₀ U (S) + (1 – p₀) U(s). (4.1)

Рассчитаем полезность результатов любого из возможных исходов для задачи 4.1. Пусть для ЛПР безразлично: потерять 20 000 дол. или принять участие в игре (выигрыш 930 000 дол. с вероятностью 0,1 или проигрыш 50 000 дол. с вероятностью 0,9). Согласно формуле (4.1) имеем:

U (-20) = 0,1 U (930) + 0,9 U (-50) = 5,

при этом по определению принято, что U (-50) = 0, U (930) = 50, откуда следует, что U (-20) = 5.

Таким образом, если определена шкала измерения, то может быть построена функция полезности ЛПР (рис. 4.2).

Рис. 4.2. График полезности для задачи 4.

Рис. 4.3. Типы функции полезности Неймана — Моргенштерна для ЛПР, не склонного к риску (а), безразличного к риску (б), склонного к риску (в)

В общем случае график функции полезности может быть трех типов (рис. 4.3):

• для ЛПР, не склонного к риску, — строго вогнутая функция, у которой каждая дуга кривой лежит выше своей хорды (рис. 4.3 а);

• для ЛПР, безразличного к риску, — прямая линия (рис. 4.3 б),

• для ЛПР, склонного к риску, — строго выпуклая функция, у которой каждая дуга кривой лежит ниже своей хорды (рис. 4.3 в).

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: