 |
Пример №8. Поскольку поворот — это движение, то образом прямой будет прямая. Подобие фигур
|
|
|
|
Пример №8
Даны прямая 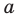 и точка
и точка 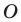 вне ее. Постройте образ прямой
вне ее. Постройте образ прямой  при повороте вокруг точки
при повороте вокруг точки 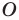 против часовой стрелки на угол
против часовой стрелки на угол 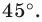

Решение:
Поскольку поворот — это движение, то образом прямой 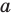 будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой 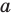 произвольные точки
произвольные точки  (рис. 19. 15). Построим точки
(рис. 19. 15). Построим точки  — их образы при повороте вокруг точки
— их образы при повороте вокруг точки  против часовой стрелки на угол
против часовой стрелки на угол  Тогда прямая
Тогда прямая 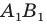 — образ прямой
— образ прямой 
Пример №9
Точка 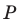 принадлежит углу
принадлежит углу  но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой
но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой 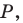 а две другие принадлежат сторонам
а две другие принадлежат сторонам 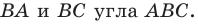
Решение:
Пусть прямая  — образ прямой
— образ прямой 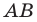 при повороте вокруг центра
при повороте вокруг центра 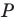 против часовой стрелки на угол
против часовой стрелки на угол  (рис. 19. 16). Обозначим буквой
(рис. 19. 16). Обозначим буквой  точку пересечения прямых
точку пересечения прямых 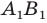 и
и 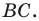
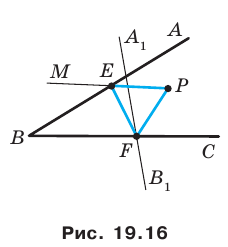
Пусть точка 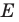 — прообраз точки
— прообраз точки 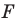 при рассматриваемом повороте. Точка
при рассматриваемом повороте. Точка  принадлежит стороне
принадлежит стороне 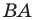 угла
угла 
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую  как образ прямой
как образ прямой  при повороте вокруг центра
при повороте вокруг центра 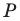 против часовой стрелки на угол
против часовой стрелки на угол 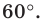 Пусть
Пусть 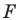 — точка пересечения прямых
— точка пересечения прямых 
Строим угол  равный
равный  Пусть прямые
Пусть прямые 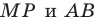 пересекаются в точке
пересекаются в точке 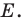 Эта точка и является прообразом точки
Эта точка и является прообразом точки 
Имеем:  Следовательно, треугольник
Следовательно, треугольник 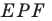 равносторонний.
равносторонний. 
Подобие фигур
На рисунке 20. 1 изображены точки  такие, что
такие, что  Говорят, что точка
Говорят, что точка 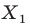 — это образ точки
— это образ точки  при гомотетии с центром
при гомотетии с центром  и коэффициентом 2.
и коэффициентом 2. 
На рисунке 20. 2 изображены точки  такие, что
такие, что  Говорят, что точка
Говорят, что точка  — это образ точки
— это образ точки  при гомотетии с центром
при гомотетии с центром 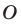 и коэффициентом
и коэффициентом 
Вообще, если точки  таковы, что
таковы, что 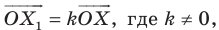 то говорят, что точка
то говорят, что точка  — это образ точки
— это образ точки  при гомотетии с центром
при гомотетии с центром 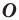 и коэффициентом
и коэффициентом 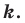
Точку  называют центром гомотетии, число
называют центром гомотетии, число 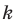 — коэффициентом гомотетии,
— коэффициентом гомотетии, 
|
|
|
Рассмотрим фигуру 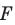 и точку
и точку  Каждой точке
Каждой точке  фигуры
фигуры  поставим в соответствие точку
поставим в соответствие точку  являющуюся образом точки
являющуюся образом точки 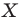 при гомотетии с центром
при гомотетии с центром  и коэффициентом
и коэффициентом  (если точка
(если точка 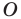 принадлежит фигуре
принадлежит фигуре  то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры  получим фигуру
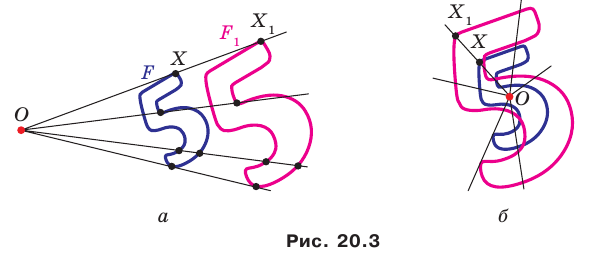
получим фигуру 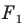 (рис. 20. 3). Такое преобразование фигуры
(рис. 20. 3). Такое преобразование фигуры  называют гомотетией с центром
называют гомотетией с центром и коэффициентом
и коэффициентом 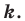 Также говорят, что фигура
Также говорят, что фигура  гомотетична фигуре
гомотетична фигуре  с центром
с центром 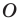 и коэффициентом
и коэффициентом 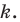
Например, на рисунке 20. 4 треугольник  гомотетичен треугольнику
гомотетичен треугольнику 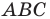 с центром
с центром  и коэффициентом, равным -3.
и коэффициентом, равным -3.
можно сказать, что треугольник  гомотетичен треугольнику
гомотетичен треугольнику  с тем же центром, но коэффициентом гомотетии, равным
с тем же центром, но коэффициентом гомотетии, равным 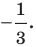
Отметим, что при  гомотетия с центром
гомотетия с центром  является центральной симметрией с центром
является центральной симметрией с центром  (рис. 20. 5). Если
(рис. 20. 5). Если 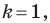 то гомотетия является тождественным преобразованием.
то гомотетия является тождественным преобразованием.
Очевидно, что при  гомотетия не является движением.
гомотетия не является движением.

Теорема 20. 1. При гомотетии фигуры  с коэффициентом
с коэффициентом  все расстояния между ее точками изменяются в
все расстояния между ее точками изменяются в 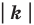 раз, то есть если
раз, то есть если  — произвольные точки фигуры
— произвольные точки фигуры  а точки
а точки  и
и  — их соответствующие образы при гомотетии с коэффициентом
— их соответствующие образы при гомотетии с коэффициентом 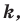 то
то 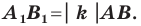
Доказательство: Пусть точка  — центр гомотетии. Тогда
— центр гомотетии. Тогда 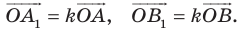 Имеем:
Имеем: 
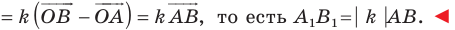
Следствие. Если треугольник 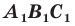 гомотетичен треугольнику
гомотетичен треугольнику  с коэффициентом гомотетии
с коэффициентом гомотетии 
Для доказательства этого утверждения достаточно воспользоваться теоремой 20. 1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
- образом прямой является прямая;
- образом отрезка является отрезок;
- образом угла является угол, равный данному;
- образом треугольника является треугольник, подобный данному;
- образом окружности является окружность;
- площадь многоугольника изменяется в
 раз, где
раз, где  — коэффициент гомотетии.
— коэффициент гомотетии.
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
|
|
|
На рисунке 20. 6 фигура  гомотетична фигуре
гомотетична фигуре  а фигура
а фигура  симметрична фигуре
симметрична фигуре  относительно прямой
относительно прямой 
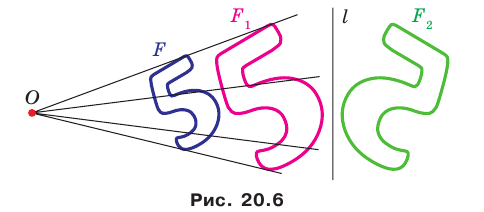
Говорят, что фигура  получена из фигуры
получена из фигуры 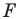 в результате композиции двух преобразований: гомотетии и осевой симметрии.
в результате композиции двух преобразований: гомотетии и осевой симметрии.
Поскольку  то фигуры
то фигуры 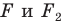 имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура
имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура  получена из фигуры
получена из фигуры  в результате преобразования подобия.
в результате преобразования подобия.
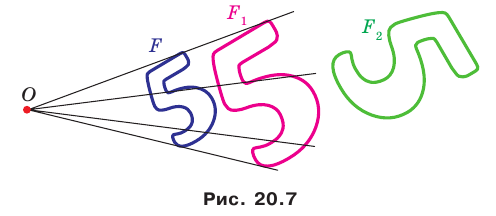
На рисунке 20. 7 фигура 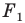 гомотетична фигуре
гомотетична фигуре  а фигура
а фигура  — образ фигуры
— образ фигуры 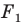 при некотором движении. Здесь также можно утверждать, что фигуры
при некотором движении. Здесь также можно утверждать, что фигуры  подобны.
подобны.
Из сказанного следует, что целесообразно принять такое определение.
|
|
|


