 |
Определение производной. Геометрический и физический смысл.
|
|
|
|
Лекции 4 Производная функции одной переменной. Дифференциал
Содержание лекции: Задачи, приводящие к понятию производной. Определение производной, геометрический и физический смысл. Дифференцируемость функции в точке. Дифференциал функции, его приложения. Линеаризация функции. Правила дифференцирования. Таблица производных. Производные функций, заданных неявно и параметрически. Производные высших порядков.
1. Задачи, приводящие к понятию производной
Задача о скорости: Пусть материальная точка М движется по прямой. Положение ее определяется расстоянием S, отсчитываемым от некоторой «начальной» точки О. Время движения t отсчитывается от некоторого начального момента (причем, совсем не обязательно, чтобы точка М в этот момент находилась в точке О). Очевидно, S есть функция времени t. Движение считается вполне заданным, если известно уравнение движения: S = f (t). Это уравнение называют законом движения точки.
 Найдем мгновенную скорость точки М, т.е. ее скорость в заданный момент времени t. Придадим переменной t некоторое приращение D t и рассмотрим момент времени t + D t, когда точка окажется в положении М1.
Найдем мгновенную скорость точки М, т.е. ее скорость в заданный момент времени t. Придадим переменной t некоторое приращение D t и рассмотрим момент времени t + D t, когда точка окажется в положении М1.
Приращение пути ММ1 за промежуток D t обозначим DS, причем
DS = f (t +D t) – f (t).
Разделим обе части этого равенства на D t. Тогда  есть средняя скорость v ср точки на участке ММ1, т.е. за промежуток времени D t: v ср =
есть средняя скорость v ср точки на участке ММ1, т.е. за промежуток времени D t: v ср =  . Эта скорость меняется вместе с изменением D t, причем, чем меньше D t, тем лучше v ср характеризует скорость движения точки М в момент t. Исходя из этого, скоростью v точки в момент времени t (мгновенной скоростью) называют предел, к которому стремится средняя скорость v ср при D t ® 0. Таким образом,
. Эта скорость меняется вместе с изменением D t, причем, чем меньше D t, тем лучше v ср характеризует скорость движения точки М в момент t. Исходя из этого, скоростью v точки в момент времени t (мгновенной скоростью) называют предел, к которому стремится средняя скорость v ср при D t ® 0. Таким образом,
 .
.
 Следовательно, задача об отыскании мгновенной скорости точки сводится к вычислению предела отношения приращения пути к приращению времени, когда последнее стремится к нулю.
Следовательно, задача об отыскании мгновенной скорости точки сводится к вычислению предела отношения приращения пути к приращению времени, когда последнее стремится к нулю.
|
|
|
Задача о касательной. Прежде чем сформулировать задачу, дадим определение касательной. Рассмотрим кривую L, и пусть М – какая-либо точка этой кривой. Рассмотрим еще одну точку М1 кривой L и проведем секущую ММ1. Когда точка М1 будет перемещаться вдоль кривой L, приближаясь к М, секущая ММ1 будет менять свое положение и стремится к положению МТ.
Касательной к кривой L в точке М называется предельное положение секущей ММ1, когда точка М1 вдоль кривой стремится к точке М.
Из этого определения следует, что угол М1МТ стремится к нулю, когда к нулю стремится хорда ММ1.
Не всякая кривая в любой своей точке может иметь касательную:
 | |||||
 | |||||
 | |||||
Пусть непрерывная кривая L задана уравнением у = f (x), а М(х, у) – некоторая точка этой кривой. Имеет ли заданная кривая касательную в точке М?
Рассмотрим на этой кривой точку М1(х +D х; у + D у) и проведем секущую ММ1.
 |
 Секущая образует с осью ОХ угол b. Из рисунка видно, что
Секущая образует с осью ОХ угол b. Из рисунка видно, что  . Но когда D х ® 0, точка М1 вдоль кривой стремится к точке М, |MM1| ® 0, секущая ММ1 стремится занять положение касательной МТ, а Ð М1МТ® 0. При этом угол Ð b = Ða + ÐМ1МТ стремится к Ða. Значит,
. Но когда D х ® 0, точка М1 вдоль кривой стремится к точке М, |MM1| ® 0, секущая ММ1 стремится занять положение касательной МТ, а Ð М1МТ® 0. При этом угол Ð b = Ða + ÐМ1МТ стремится к Ða. Значит,
 .
.
Таким образом, чтобы ответить на вопрос, существует ли касательная к кривой у = f (x) в заданной точке М, нужно убедиться в существовании конечного или бесконечного предела отношения приращения функции f (x) к приращению аргумента в этой точке, при стремлении приращения аргумента к нулю.
Обе рассмотренные задачи привели к необходимости вычисления предела по существу одного и того же типа: отношения приращения одной величины к приращению другой, когда последнее стремится к нулю.
Поэтому есть смысл изучать подобные пределы, абстрагируясь от конкретной природы вопроса.
|
|
|
Определение производной. Геометрический и физический смысл.

Пусть функция у = f (x) определена на множестве D. Возьмем некоторое значение х Î D аргумента и придадим ему приращение D х (положительное или отрицательное) так, чтобы х + D х Î D. Тогда значение функции у = f (x) в начальной точке изменится и станет равным у + D у = f (х + D х), т.е. функция получит приращение D у = f (х + D х) – f (x) (рис.).
Определение 4.1. Предел отношения приращения D у функции у = f (x) к вызвавшему его приращению D х аргумента при стремлении D х к нулю называется производной функции у = f (x) в точке х и обозначается f ¢(x).
Таким образом,
 . (1)
. (1)
Наряду с обозначением f ¢(x), используется обозначения
у ¢, ух ¢,  ,
, 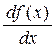 ,
, 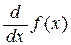 .
.
Равенство (1) определяет правило (закон) по которому каждому значению х ÎD ставится в соответствие конечное или бесконечное значение производной, т.е. производная есть функция переменной х.
Используя определение производной, можно теперь сказать, что скорость движущейся точки в каждый момент времени есть производная от пути по времени. Если эту физическую иллюстрацию обобщить на случай произвольной функции, рассматривая изменение функции как пройденный путь, а изменение аргумента как время, то получим
Физический смысл производной: производная функции есть скорость изменения функции при изменении ее аргумента.
Аналогично, используя результаты задачи о касательной, получим
Геометрический смысл производной: производная функции у = f (x) в точке х есть тангенс угла наклона к оси ОХ касательной, проведенной к графику функции в точке (х, f (x)).
Теорема 4.1.(необходимое условие существования производной)
Если функция у = f (x) имеет в точке х 0 производную, то она непрерывна в этой точке.
Доказательство: Если для функции у = f (x) в точке х 0 существует производная, то существует предел
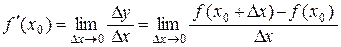
Если этот предел конечный, то по теореме 2.4 имеем
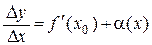 ,
,
где a(х) есть бесконечно малая при D х ® 0. Отсюда получаем
D у = f ¢(x 0)D x + a(x)D x.
Рассмотрим
 = 0,
= 0,
а это, согласно второму определению непрерывности функции в точке, означает, что функция у = f (x) непрерывна в точке х 0.
Предположим теперь, что  = + ¥ (или –¥), причем это возможно тогда и только тогда, когда односторонние пределы бесконечны и одинакового знака. Пусть, для определенности,
= + ¥ (или –¥), причем это возможно тогда и только тогда, когда односторонние пределы бесконечны и одинакового знака. Пусть, для определенности,
|
|
|

Тогда  и
и  .
.
Но это означает, что числитель и знаменатель дроби имеют одинаковый знак. В первом случае f (х 0 + D х) – f (x 0) > 0, т.к.D х ® +0, т.е. D х > 0. Во втором случае f (х 0 + D х) – f (x 0) < 0 при D х < 0. А такое возможно только если
f (х 0 + D х) ® f (x 0) при х ® х 0,
т.е. функция у = f (x) непрерывна в точке х 0. ЧТД.

 Случай бесконечной производной графически можно представить так:
Случай бесконечной производной графически можно представить так:
Таким образом, в каждой точке, в которой существует производная функции, эта функция обязательно непрерывна. Обратное утверждение неверно, т.е. из непрерывности функции в точке не следует существование в этой точке конечной производной. Продемонстрируем это на примере.
 Рассмотрим функцию
Рассмотрим функцию

Эта функция непрерывна в точке х 0 = 1, т.к.
f (1) = 1,
f (1+0) =  = 1,
= 1,
f (1– 0) =  = 1.
= 1.
Но в этой точке не существует производная функции. Действительно, если D х = х – 1> 0, то
 .
.
Если же D х = х – 1< 0, то

Значит, 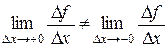 , а это, согласно критерию существования предела означает, что
, а это, согласно критерию существования предела означает, что  не существует.
не существует.
Заметим, что в этом случае можно говорить о существовании односторонних производных:
f ¢(x 0+0) = 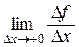 и f ¢(x 0 –0) =
и f ¢(x 0 –0) = 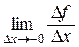 .
.
Тогда существование производной функции f (x) в точке x 0 равносильно существованию f ¢(x 0+0), f ¢(x 0 –0) и выполнению условия f ¢(x 0+0) = f ¢(x 0 –0).
В рассмотренном примере f ¢(1+0) = 2, f ¢(1 –0) = 1.
Дифференцируемость функции в точке. Правила дифференцирования. Таблица производных.
Дадим еще одно важное
Определение 4.2.
Функция у = f (x) называется дифференцируемой в точке х 0, если ее приращение D у в этой точке, соответствующее приращению D х, представимо в виде D у = А.D х + о(D х), где А – некоторая константа.
Справедлива
Теорема 4.2. (критерий дифференцируемости)
Функция у = f (x) дифференцируема в точке х 0 тогда и только тогда, когда она в этой точке имеет конечную производную.
Доказательство: 1) Достаточность. Пусть функция у = f (x) дифференцируема в точке х 0. Значит, ее приращение в этой точке представимо в виде
D у = А.D х + о(D х),
|
|
|
где А – некоторая константа. Разделим обе части этого равенства на D х и перейдем к пределу при D х ® 0:
 .
.
Значит, данная функция в точке х 0 имеет конечную производную, равную А.
2) Необходимость. Если функция у = f (x) в точке х 0 имеет конечную производную, т.е.  , то согласно теореме 2.4,
, то согласно теореме 2.4,
 , откуда D у = f ¢(x 0)D x + a(x)D x,
, откуда D у = f ¢(x 0)D x + a(x)D x,
где a(х) – бесконечно малая при D х ® 0.
Так как  , то a(x)D x = о(D х). Значит,
, то a(x)D x = о(D х). Значит,
D у = А.D х + о(D х), где А = f ¢(x 0). ЧТД.
Таким образом, понятия «дифференцируемая функция» и «функция, имеющая конечную производную» – равносильные. Поэтому операцию нахождения производной называют дифференцированием.
Функция f (x) дифференцируема на множестве Х, если она имеет производную в каждой точке этого множества.
Основные правила дифференцирования вам известны еще из школьного курса, поэтому здесь мы их только напомним (доказательство этих правил разберите самостоятельно). Пусть с -постоянная, u = u(x) и v = v(x) – дифференцируемые функции. Тогда
1. (с)¢ = 0
2. (c×u)¢ = c×u¢
3. (u + v)¢ = u¢ + v¢
4. (u - v)¢ = u¢ - v¢
5. (u× v)¢ = u¢v + uv¢
6. 
6.а. 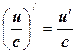
7. (F (u (x)))¢ = F ¢(u)× u ¢(x)
8. 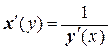 , если у (х) и х (у) – взаимно обратные функции.
, если у (х) и х (у) – взаимно обратные функции.
Докажемдва последних правила:
7) Если функция и = и (х) дифференцируема в точке х 0, а функция у = F(u) имеет производную в точке и 0 = и (х 0), то функция F(u(x))имеет производную в точке х 0, причем
(F(u(x 0)))¢ = F ¢(u 0)× u ¢ (x 0)
Доказательство: Пусть х = х 0, придадим переменной х приращение D х и рассмотрим точку х 0 + D х. Тогда функция и = и (х) получит приращение
D и = и (х 0 + D х) – и (х 0).
Этому приращению будет соответствовать приращение
DF = F(u 0+D и) – F(u 0).
Причем, в силу существования производных заданных функций, а следовательно, их непрерывности в соответствующих точках, имеем
D х ® 0 Þ D и ® 0 Þ DF ® 0.
Поскольку
 , то
, то  ,
,
где a бесконечно малая при D и ® 0, а, значит, и при D х ® 0. Из этого равенства имеем
DF = F ¢(u 0)×D и + aD и.
Разделив обе части этого равенства на D х, и переходя к пределу при D х ®0, получим
F ¢(х 0) = 
=  . ЧТД.
. ЧТД.
8) Если функция у = у (x) и ее обратная х = х (y) дифференцируемы, причем у ¢(x) ¹ 0, то

Доказательство: По определению обратной функции, х (y (х)) = х для всех х из области определения этой функции. Поэтому, согласно предыдущей теореме,
(х (y (х)))¢ = х ¢(у). у ¢(х) = 1,
откуда и следует равенство  . ЧТД.
. ЧТД.
Заметим, что в доказательстве использован известный из школьного курса факт, что производная независимой переменной равна 1. Доказательство этого факта очень просто: если у = х, то по определению
у ¢ = х ¢ = 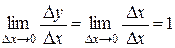 .
.
Кроме правил вычисления производной, в школе вы доказывали и использовали формулы вычисления производных основных элементарных функций. Сведем эти формулы в единую таблицу, которую следует заучить наизусть.
|
|
|
В левой колонке таблицы указаны производные основных элементарных функций, а в правой – производные сложной функции соответствующего вида.
| Таблица производных основных элементарных функций x - независимая переменная, u = и (х) – дифференцируемая функция, | |
1.1. х ¢ = 1
1.2.  1.3.
1.3.  1.4.
1.4.  1.5.
1.5. 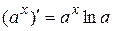 1.6.
1.6.  1.7.
1.7.  1.8. (sin x)¢ = cos x
1.9. (cos x)¢ = – sin x
1.10.
1.8. (sin x)¢ = cos x
1.9. (cos x)¢ = – sin x
1.10.  1.11.
1.11.  1.12.
1.12.  1.13.
1.13.  1.14.
1.14.  1.15.
1.15. 
|
2.2.  2.3.
2.3. 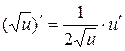 2.4.
2.4. 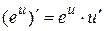 2.5.
2.5.  2.6.
2.6.  2.7.
2.7. 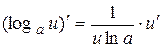 2.8. (sin и)¢ = cos и × и ¢
2.9. (cos u)¢ = – sin и× и ¢
2.10.
2.8. (sin и)¢ = cos и × и ¢
2.9. (cos u)¢ = – sin и× и ¢
2.10.  2.11.
2.11. 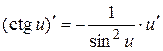 2.12.
2.12.  2.13.
2.13.  2.14.
2.14.  2.15.
2.15. 
|
|
|
|


