 |
Спектральная плотность импульсного дискретного сигнала.
|
|
|
|
Дискретный сигнал, представленный в форме (18.1) представляет собой произведение:
(18.2)
образованной дельта импульсами, следующими через интервалы D и исходного сигнала х(t). Спектр произведения двух сигналов, как известно, выражается через свёртку их спектральных плотностей. Поэтому если известны спектры исходных сигналов 
и 
, то спектральная плотность дискретного сигнала будет: 
(18.3)
Представим периодическую функцию h(t) в виде ряда Фурье: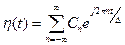 
. Коэффициенты этого ряда: 
(18.4)
Таким образом, получили: 
(18.5)
Для сигнала в виде экспоненты спектральная плотность, как известно: 
(7.18)
т.е. спектральная плотность функции h(t) будет: 
(18.6)
т.е. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта-импульсов в частотной области, расположенных через интервалы 
.
Подставив значение Sh(w) в формулу 18.3 и изменив порядок суммирования и интегрирования получим: 
(18.7)
Итак, спектр дискретизированного сигнала представляет собой с точностью до масштабного множителя 
результат суммирования бесконечного числа значений спектра исходного сигнала. Эти значения располагаются на оси частот через интервалы 
, равные значению частоты дискретизации. На рис.18.2а) показан спектр исходного сигнала, а на рис.18.2б) спектр продискретизированного дельта - импульсами сигнала при выборе достаточно высокой частоты дискретизации 
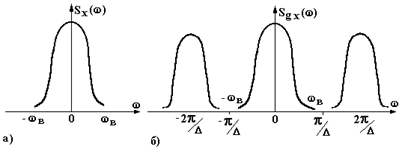Из рисунка видно, что спектр продискретизированного сигнала по форме повторяет спектр исходного сигнала вблизи частот 
. При малой частоте дискретизации спектральные диаграммы на рис.18.2б) могут пересекаться и в этом случае возникают при восстановлении сигнала
Рис. 18.2
ошибки. При большой же частоте дискретизации с помощью фильтров сигнал, в соответствии с теоремой Котельникова, может быть восстановлен без ошибок. Если дискретизирующий сигнал имеет форму отличающуюся от дельта - импульсов, то в этом случае максимумы спектральных диаграмм на рис.18.2б) будут не постоянными и расположатся по огибающей повторяющей форму спектральной диаграммы дискретизирующих импульсов. Этот случай больше соответствует практике дискретизации сигналов.
|
|
|
57. ТЕОРИЯ Z- ПРЕОБРАЗОВАНИЯ.
Для определения Z - преобразования воспользуемся выражением для ДПФ дискретного сигнала рассмотренного в лек. 18 (формула 18.10), записав его в виде:
(18.10)
Вводя новое обозначение 
этот ряд можно переписать в виде: 
(19.1)
В такой форме полученная сумма носит название Z - преобразования последовательности дискретных сигналов 
. Новая переменная Z представляет собой комплексное число. Использование Z - преобразования позволяет перейти в задачах анализа от трансцендентных функций еpt к алгебраическим рядам с комплексной переменной Z.
Рассмотрим несколько простых примеров.
1. Допустим сигнал задан в виде дельта - функции: 
В этом случае 
(19.2)
Смещение на один такт во временной области соответствует умножению на Z-1 в области Z - изображения, на два такта на Z-2 и т.д.
2. Дискретный сигнал моделирует скачок напряжения 
. Учитывая что при сдвиге происходит умножение на Z-n получим бесконечный ряд: 
, который сходится при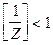 
. Если рассматривать этот ряд как геометрическую прогрессию со знаменателем 
, то получим Z - преобразование скачка в виде: 
(19.3)
3.Экспоненциальная функция 
при подстановке в ряд (19.1) и использовании формулы суммы геометрической прогрессии даёт:
(19.4)
Свойства Z - преобразования обстоятельно исследованы и разработаны таблицы Z - преобразований для многих известных функций.
58.СВОЙСТВА Z- ПРЕОБРАЗОВАНИЯ.
1. Линейность. Если {xK} и {yK} - две числовые последовательности, отображающие некоторые дискретные сигналы, причем известны соответствующие Z - преобразования X(Z) и Y(Z), то сигналу 
соответствует Z - преобразование справедливое при любых a и b и равное:
|
|
|
(19.7)
2. Z - преобразование смещенного сигнала. Рассмотрим дискретный сигнал {YK}, получившийся из дискретного сигнала {XK} путем сдвига на одну позицию в сторону запаздывания, т.е. когда YK=XK-1. Непосредственное вычисление Z - преобразования приводит к следующему результату:
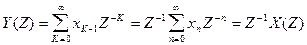(19.8)
Таким образом, умножение на Z-1 характеризует задержку на один интервал дискретизации в Z - области.
3. Z - преобразование свертки. Пусть x(t) и y(t) - непрерывные сигналы, для которых определена свертка: 
(19.9)
По аналогии с этим выражением для дискретных сигналов можно записать выражение для дискретной свертки {fK} - последовательность чисел, общий член которой:
(19.10)
Вычислим Z - преобразование дискретной свертки:
(19.11)
Итак, свертке двух дискретных сигналов соответствует произведение их Z - преобразований.
|
|
|
