 |
Вариационные задачи на условный экстремум
|
|
|
|
Классификация вариационных задач.
Вариационная задача означает нахождение функции (в рамках вариационного исчисления — уравнения на функцию), удовлетворяющей условию стационарности некоторого заданного функционала, то есть такой функции, (бесконечно малые) возмущения которой не вызывают изменения функционала по крайней мере в первом порядке малости. Также вариационной задачей называют тесно связанную с этим задачу нахождения функции (уравнения на функцию), на которой данный функционал достигает локального экстремума (во многом эта задача сводится к первой, иногда практически полностью). Обычно при таком употреблении терминов подразумевается, что задача решается методами вариационного исчисления.
Типичными примерами вариационной задачи являются изопериметрические задачи в геометрии и механике; в физике — задача нахождения уравнений поля из заданного вида действия для этого поля.
Изопериметрическими являются две классические задачи вариационного исчисления:
Задача Дидоны и задача о цепной линии.
Зада́ча Дидо́ны — исторически первая задача вариационного исчисления. адача сводится к нахождению экстремума функционала
с граничными условиями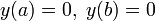 
, и при фиксированном параметре (длине)
a и b просто точки закрепления каната. Решением является дуга окружности, если концы нельзя двигать по побережью, и полуокружность в противном случае.
Задача Бо́льца — это задача теории оптимального управления вида
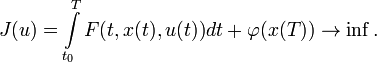
Простейшей задачей классического вариационного исчисления называется следующая экспериментальная задача в пространстве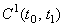 
:
(7.1)
‑ называется интегрантом. Экстремум в задаче (7.1) рассматривается среди функций 
, удовлетворяющих условиям на концах, или краевым условиям 
, такие функции 
называются допустимыми.
|
|
|
Лагранжа задача - одна из основных задач классич. вариационного исчисления. Состоит в минимизации функционала
при наличии дифференциальных ограничений типа равенств:
и граничных условий:
Обычно Л. з. рассматривается при условии, что имеет место регулярность системы (1), состоящая в том, что матрица 
имеет максимальный ранг:
Задачей с подвижными концами называется следующая задача в пространстве 
:
(8.1)
, 
(8.2)
Здесь 
– заданный конечный отрезок, 
– функция трех, а 
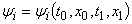– четырёх переменных.
Задача оптимального управления заключается в нахождении функций состояния x(t) и управления u(t) для времени 
, которые минимизируют функционал.
Уравнения состояния: 
(1).
Граничные условия 
, 
(2).
Минимизируемый функционал: 
.
здесь x(t) — вектор состояния u(t) — управление, t0,t1 — начальный и конечный моменты времени.
Задача со старшими производными.
Задача о брахистотроне и быстродействии.
Необходимое условие экстремума. Уравнение Эйлера.
Функционал Лагранжа.
Задача Лагранжа: определить минимум функционала
при условии
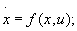
фазовый вектор x (t) должен удовлетворять ещё некоторым граничным условиям.
В своей классической постановке условия задачи Лагранжа не предусматривают никаких ограничений на управление u (t). Выше (см. раздел Условный экстремум. Задача Лагранжа) подчёркивалась тесная связь между задачей Лагранжа и задачей управления. В рассмотренном там примере u (t) — тяга ракетного двигателя. Эта величина подчинена ограничениям: тяга двигателя не может превосходить некоторой величины, и угол поворота вектора тяги также ограничен. В данном конкретном примере компонента ui (i = 1,2,3) вектора тяги двигателя подчинена ограничениям
где а-i и a+i — некоторые заданные числа. Подобных примеров можно привести много.
Таким образом, в технике появилось много задач, которые сводятся к задаче Лагранжа, но при дополнительных ограничениях типа (10), записываемых в форме u Î Gu, где Gu — некоторое множество, которое, в частности, может быть замкнутым. Такие задачи получили название задач оптимального управления. В задаче Лагранжа можно исключить управление u (t) при помощи уравнения (8) и получить систему уравнений, которая содержит только фазовую переменную х и множитель Лагранжа j. Для теории оптимального управления должен был быть разработан специальный аппарат. Эти исследования привели к открытию принципа максимума Л. С. Понтрягина. Он может быть сформулирован в форме следующей теоремы: для того чтобы функции 
и 
были решением задачи оптимального управления чтобы они доставляли минимум функционалу (9)], необходимо, чтобы u (t) доставляла максимум функции Гамильтона
где y — множитель Лагранжа (импульс), который является ненулевым решением векторного уравнения
Принцип максимума позволяет свести задачу оптимального управления к краевой задаче для системы обыкновенных дифференциальных уравнений порядка 2n (n — размерность фазового вектора). Принцип максимума и в этом случае даёт более сильный результат, чем теорема Лагранжа, поскольку он требует, чтобы 
было не стационарным значением функции Гамильтона Н, а доставляло максимум Н.
|
|
|
Вариационные задачи на условный экстремум
Основные виды задачи на условный экстремум, которые имеет смысл рассмотреть, таковы:
· Надо найти экстремум функционала 
при условии равенства нулю другого функционала 
; (то, что в правой части нуль, не нарушает общности).
· Надо найти экстремум функционала при условии 
.
· Надо найти экстремум функционала при условии выполнения для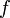 
уравнения 
, где 
— некоторая функция 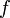и/или производных 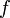, обозначенных штрихами.
(Третий тип условия выписан здесь не в самом общем виде, но для наших целей этого достаточно.)
К первым двум случаям практически прямо (на принятом сейчас нами уровне строгости нет смысла проводить тут границу между случаем функций конечномерного аргумента, и функционалами) применим метод неопределенных множителей Лагранжа. А именно, для нахождения условного экстремума при наложении соответстсующих условий, нужно решить вариационную задачу для функционала 
в первом и 
во втором случае, а затем подобрать (решив уравнение 
в первом случае и N уравнений с частными производными по каждому из λi во втором) такие λ, которые реализуют минимум в найденном семействе функций f, для котого эти λ являются параметрами. То есть, что касается вариационного исчисления, то ключевым моментом является нахождение и приравнивание нулю вариации (или вариационной производной) для некоего нового функционала 
, для этих двух случаев:
|
|
|
Третий же случай рассмотрим здесь для интегрального функционала 
. Тогда нахождение условного экстремума сводится сначала к варьированию функционала
,
где x — переменная, принадлежащая области интегрирования Ω (одномерной или n-мерной), аλ(x) — некая неопределенная функция x, которая войдет в уравнение, полученное после вычисления вариационной производной и приравнивания ее нулю.
Обоснованием такого решения для случая 3 может служить представление для каждой точкиx0 из Ω выполнения равенства 
в x0 как приравнивание нулю функционала 
с использованием дельта-функции Дирака. Далее можно считать на рассматриваемом здесь неформальном уровне очевидным, что задача стала аналогичной варианту 2, и, после суммирования по всем x0, ее решение сводится к описанному выше.
Таким образом, ключевой момент с точки зрения вариационного исчисления в нахождении условного экстремума третьего типа сводится к
3. 
Под производными при многомерном x можно иметь в виду, например, частные производные разного порядка, в том числе смешанные.
|
|
|
