 |
Частная и множественная корреляция
|
|
|
|
Частная и множественная корреляция обычно рассматриваются при изучении совокупности многомерных измерений. Рассмотрим её кратко на промере трёхмерного пространства.
Пусть имеем три переменные – x, y, z.
Частным коэффициентом корреляции между x и y при фиксированном значении z или, другими словами, при исключении влияния на них переменной z является величина, определяемая из выражения:
 =
=  .
.
Остальные частные коэффициенты корреляции определяются путём замены в приведённой формуле соответствующих индексов.
Частные коэффициенты корреляции можно рассчитать, рассматривая корреляцию не непосредственно между переменными, а между отклонениями, в которых влияние других переменных исключено.
Для трёх переменных это выглядит следующим образом. Пусть х и у корреляционно зависят от z. Выразим эту зависимость в виде:  = f1(z),
= f1(z),  = f2(z). Рассмотрим разности ех = (x -
= f2(z). Рассмотрим разности ех = (x -  ) и еу = (y -
) и еу = (y -  ). Ясно, что в них влияние переменной z исключено, поэтому коэффициент корреляции между остатками ех и еу будет отражать связь между исходными переменными х и у с исключением влияния переменной z. Таким образом
). Ясно, что в них влияние переменной z исключено, поэтому коэффициент корреляции между остатками ех и еу будет отражать связь между исходными переменными х и у с исключением влияния переменной z. Таким образом  =
=  .
.
Частные коэффициенты корреляции обладают всеми свойствами парных коэффициентов корреляции. Они служат показателями чистой линейной корреляционной связи между переменными с исключением влияния учтённых переменных.
Частная корреляция очищает взаимосвязи между переменными от опосредованных зависимостей и помогает обнаружить величины, которые усиливают или ослабляют связи между конкретными переменными.
В развитие дальнейшего рассмотрения корреляции распространим понятие корреляционной связи на более чем две переменные. Тесноту линейной корреляционной связи между одной переменной и несколькими другими измеряют с помощью коэффициента множественного корреляции. Множественный коэффициент корреляции, например, между величиной z и двумя величинами x и y определяется по формуле
|
|
|
 .
.
Такой коэффициент заключён между нулём и единицей и равен единице, когда связь между величинами z и (x,y) является линейной функциональной, и равен нулю, если линейная связь между z и (x,y) отсутствует. Другие множественные коэффициенты корреляции определяются путём замены соответствующих индексов в приведённой формуле.
Коэффициент множественный корреляции можно определить, рассчитав коэффициент корреляции между z и  , где
, где  = f(x,y) –модельные значения z, вычисленные по уравнению регрессии от х и у. Таким образом
= f(x,y) –модельные значения z, вычисленные по уравнению регрессии от х и у. Таким образом 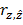 =
=  .
.
Понятия частного и множественного коэффициентов корреляции можно распространить на случай более 3 переменных. Вычисляются они на основе матрицы парных коэффициентов корреляции.
Так, коэффициент частной корреляции между переменными x i и x j при фиксированных значениях всех остальных рассматриваемых переменных X(i,j) рассчитывается из соотношения
ri,j.X(i,j) = –Ri,j / (RiiRjj)1/2,
а коэффициент множественной корреляции между переменной x i и всеми другими переменными X(i), т. е. коэффициент Ri.X(i) рассчитывается из соотношения
Ri. X (i) =  .
.
Здесь Rkl – алгебраическое дополнение для элемента rkl в определителе корреляционной матрицы R анализируемых признаков, а det R – определитель этой матрицы.
При определении значимости частных коэффициентов корреляции пользуются теми же методами, что и для парных коэффициентов корреляции, уменьшая число степеней свободы на число исключаемых переменных, а для множественных коэффициентов корреляции используется F-статистика:
F = 
 ,
,
где m – число анализируемых переменных.
При верности гипотезы о равенстве нулю коэффициента множественной корреляции F-статистика следует распределению Фишера с числом степеней свободы числителя, равным m, и знаменателя, равным n – m – 1.
|
|
|
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации. Коэффициент множественной детерминации показывает долю вариации одной переменной, обусловленную изменением других, включенных в анализ, переменных.
|
|
|


