Примитивно рекурсивные функции (ПРФ)

Определение. Элементарными функциями называются:

1) Функция константы , где n = 0,1,2,…, q = 0,1,2,…, в частности нулевая функция .

2) Функция следования .

3) Функция выбора , где 1≤ m ≤ n, n = 1,2,…,.

Все элементарные функции - всюду определенные и алгоритмически

вычислимые. Имеется небольшое число операций над элементарными функциями, переводящими вычислимые функции снова в вычислимые.

Операция подстановки (суперпозиции)

Пусть задана функция и функции . Говорят, что функция получена из этих функций с помощью операции подстановки, если выполняется следующее равенство

и обозначается 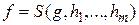, где S – означает операцию подстановки.

Пример. Пусть и . Тогда

.

Основные свойства операции подстановки

1. Операция подстановки сохраняет свойство всюду определенности функций, т. е. если функция g(y₁,…,y_m) и функции h₁(x₁,…,x_n), h₂(x₁,…,x_n), h_m (x1,…,xn) всюду определенные функции и функция f получается из них с помощью операции подстановки, то f также является всюду определенной функцией.

2. Операция подстановки сохраняет свойство алгоритмической вычислимости функций, т.е. если функции g(y1,…, ym) и h1,…,hm алгоритмически вычислимы, и f = S(g; h1,…, hm), то существует алгоритм A _f, вычисляющий функцию f.

Операция примитивной рекурсии

Пусть задана функция и функция .

Определение. Говорят, что функция получена из функций и с помощью операции примитивной рекурсии, если выполняются следующие равенства:

.

Это определение имеет смысл, когда n ≠ 0, при этом записывается

.

При задании примитивно рекурсивного описания функции , зависящей от одной переменной, схема примитивной рекурсии имеет вид

,

где .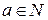

Класс ПРФ всех примитивно рекурсивных функций представляет собой множество всех функций, которые могут быть получены из простейших функций с помощью операций суперпозиции и примитивной рекурсии.

Основные свойства операции примитивной рекурсии

1) Операция примитивной рекурсии, так же как и операция подстановки, сохраняет свойство всюду определенности и алгоритмической вычислимости.

2) Сохранение алгоритмической вычислимости функций.

Пример. Применить операцию примитивной рекурсии к функции и . Функцию записать в «аналитической» форме.

Решение. , . Согласно операции примитивной рекурсии , .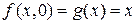

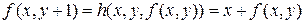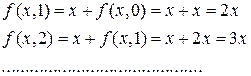
Пусть на 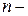ом шаге будет верным 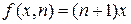. Тогда

Таким образом, в результате примитивной рекурсии .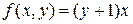

 

III. Машина Тьюринга

 

Алгоритм – это определенное на некотором языке конечное предписание (способ, рецепт), задающее дискретную последовательность исполнимых элементарных операций для решения проблемы. Процесс выполнения предписания состоит из отдельных шагов, на каждом из которых выполняется одна очередная операция.

По сути своей алгоритм есть механический процесс обработки информации. Впервые Алан Тьюринг определил понятие алгоритма исходя из понятия автоматически работающей машины; более того он предложил формальную модель такого устройства, которое интуитивно моделирует действия человека, решающего задачу, руководствуясь некоторым алгоритмом. Это устройство было названо машиной Тьюринга.

В своем вычислительном устройстве Тьюринг смоделировал доведенный до самых элементарных операций процесс выполнения произвольного алгоритма человеком. Человек имеет конечную память, и в этом смысле его можно представить системой с конечным числом состояний. Исходная информация к алгоритму обычно представляется в виде цепочки символов. Можно себе представить, что это информация представлена в виде слова (конечной последовательности символов) конечного словаря. Выполняя алгоритм, человек вычислитель использует дополнительную память (которая может быть потенциально бесконечной, например листы бумаги) для записи информации, причем эта запись производится последовательно символ за символом. При вычислениях человек может возвращаться к ранее записанной информации, стирать некоторую информацию и т.д. Таким образом, элементарными операциями при выполнении алгоритма можно считать запись и стирание символа, а также перенесение внимания с одного участка записи на другой. Предложенная Тьюрингом модель имеет одну бесконечную рабочую ленту, с которой читает и куда пишет символы и одну головку чтения-записи, которая может двигаться по рабочей ленте в любую сторону.

Машина Тьюринга работает по тактам. На каждом такте она читает символ из обозреваемой ячейки рабочей ленты, изменяет свое состояние в зависимости от своего внутреннего состояния и прочитанного символа и печатает символ в обозреваемую ячейку рабочей ленты, после чего ее головка чтения-записи может переместиться на одну позицию влево, вправо или остаться на месте. Описание функционирования МТ можно считать ее программой, которая представлена набором пятерок (команд) < s, a, p, y, D>, где s – текущее состояние, a – очередной входной сигнал, p – следующее состояние, y – очередной выходной сигнал, а D – направление перемещения головки по рабочей ленте, которое может принимать одно из трех значений Л – влево, П – вправо, Н – оставаться на месте.

Опишем теперь машину Тьюринга более тщательно. Машина располагает конечным числом знаков (символов, букв), образующих так называемый внешний алфавит А = {а0, а1..., аn}. В каждую ячейку обозреваемой ленты в каждый дискретный момент времени может быть записан только один символ из алфавита А. Ради единообразия удобно считать, что среди букв внешнего алфавита А имеется «пустая буква», и именно она записана в пустую ячейку ленты. Условимся, что «пустой буквой» или символом пустой ячейки является буква Λ. Лента предполагается неограниченной в обе стороны, но в каждый момент времени на ней записано конечное число непустых букв

Далее, в каждый момент времени машина способна находиться в одном состоянии из конечного числа внутренних состояний, совокупность которых Q = {q0, q1,.., qm}. Среди состояний выделяются два — начальное q1 и заключительное (или состояние остановки) q0. Находясь в состоянии q1, машина начинает работать. Попав в состояние q0, машина останавливается.

Работа машины определяется программой (функциональной схемой). Программа состоит из команд. Каждая команда T(i, j) (i = 1, 2,..., n; j = 0, 1,..., m) представляет собой выражение одного из следующих видов: , где , 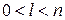и Х ={Л, П, Н}.

Как же работает машина Тьюринга? Находясь в какой-либо момент времени в не заключительном состоянии (т.е. в состоянии, отличном от q0) машина совершает шаг, который полностью определяется ее текущим состоянием qj и символом ai, воспринимаемым ею в данный момент на ленте. При этом содержание шага регламентировано соответствующей командой T(i, j): , где X = {H, П, Л}. Шаг заключается в том, что: 1) содержимое ai обозреваемой на ленте ячейки стирается и на его место записывается символ аl, (который может совпадать с ai); 2) машина переходит в новое состояние qk (оно также может совпадать с предыдущим состоянием qj); 3) машина переходит к обозрению следующей правой ячейки от той, которая обозревалась только что, если Х=П, или к обозрению следующей левой ячейки, если Х= Л, или же продолжает обозревать ту же ячейку ленты, если Х= H.

В следующий момент времени (если qk ≠ q0) машина делает шаг,

регламентированный командой T(l,k): alqk → asqrX и т.д.

Поскольку работа машины, по условию, полностью определяется ее состоянием qj в данный момент и содержимым обозреваемой в этот момент ячейки, то для каждых qj и ai, (i= 1, 2,..., n; j = 0, 1,..., m) программа машины должна содержать одну и только одну команду, начинающуюся символами qiaj. Поэтому программа машины Тьюринга с внешним алфавитом А = {Λ, а1,...,аn} и алфавитом внутренних состояний Q ={q0, q1,.., qm} содержит m(n + 1) команд.

Словом в алфавите А или в алфавите Q, или в алфавите AUQ называется любая последовательность букв соответствующего алфавита. Под k-й конфигурацией будем понимать изображение ленты машины с информацией, сложившейся на ней к началу k-го шага (или слово в алфавите А, записанное на ленту к началу k-го шага), с указанием того, какая ячейка обозревается в этот шаг, и в каком состоянии находится машина. Имеют смысл лишь конечные конфигурации, т.е. такие, в которых все ячейки ленты, за исключением, быть может, конечного числа, пусты. Конфигурация называется заключительной, если состояние, в котором при этом находится машина, заключительное.

Если выбрать какую-либо не заключительную конфигурацию машины Тьюринга в качестве исходной, то работа машины будет состоять в том, чтобы последовательно (шаг за шагом) преобразовывать исходную конфигурацию в соответствии с программой машины до тех пор, пока не будет достигнута заключительная конфигурация. После этого работа машины Тьюринга считается закончившейся, а результатом работы считается достигнутая заключительная конфигурация.

Будем говорить, что непустое слово α в алфавите А \ {Λ} = {а1,...,an} воспринимается машиной в стандартном положении, если оно записано в последовательных ячейках ленты, все другие ячейки пусты, и машина обозревает крайнюю справа ячейку из тех, в которых записано слово α. Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении, находится в начальном состоянии q1 (соответственно в состоянии остановки q0). Наконец, будем говорить, что слово α перерабатывается машиной в слово β, если от слова α, воспринимаемого в начальном стандартном положении, машина после выполнения конечного числа команд приходит к слову β, воспринимаемому в положении остановки.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: