 |
Пример решения контрольной работы
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ФИЛИАЛ МОСКОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ в г. СТАВРОПОЛЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ НАПРАВЛЕНИЯ 230100 «ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА»
Содержание
1. Методические указания по изучению курса
2. Формулировка задания и его объем
3. Таблица вариантов контрольной работы
4. Общие требования к оформлению контрольной работы
5. Порядок защиты и ответственность студента за выполнение контрольной работы
6. Контрольная работа.
7. Список рекомендуемой литературы
Методические указания по изучению курса
В процессе изучения на первом курсе студенты обязаны:
1) Прослушать курс лекций, изучить теоретический материал в соответствии с программой и написать конспект по вопросам программы.
2) Выполнить контрольную работу и представить ее в установленный срок.
При возникновении трудностей при решении отдельных задач, необходимо обратиться к преподавателю для консультаций.
В настоящем методическом пособии приведены вопросы по программе, разработанные на основе Государственного стандарта, даны примеры решения задач и задания контрольной работы.
Формулировка задания и его объем
Контрольные работы по «математическому анализу» для студентов направления 230100 «Информатика и вычислительная техника» состоит из двух частей: теоретической и практической.
|
|
|
Теоретическая часть включает в себя конспектирование в тетради ответов на все теоретические вопросы. Объем теоретической части зависит от объема самого вопроса, а также от развернутости конспекта. Конспекты являются помощью при ответе на теоретические вопросы при собеседовании по контрольной работе. Конспектом можно пользоваться и на экзамене (зачете), в том числе при решении задач в билетах или зачетных карточках. Если на некоторые теоретические вопросы студент может ответить без конспекта, то их конспектировать необязательно.
Практическая часть состоит из решения семи практических заданий. Объем этой части контрольной работы зависит от способа решения задач.
Контрольная работа считается выполненной, если законспектированы все теоретические вопросы и правильно решены все практические задания варианта.
Варианты контрольной работы
Вариант контрольной работы, а также номер задания определяется по журналу в зависимости от порядкового номера в списке группы
Общие требования к оформлению контрольной работы
При выполнении контрольной работы следует соблюдать указанные ниже правила. Работа, выполненная без соблюдения этих правил, не зачитывается и возвращается студенту для переработки.
1. Контрольную работу следует выполнять в тетради пастой любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть указаны: дисциплина, по которой выполнена контрольная работа, фамилия, имя и отчество студента, шифр группы.
3. На 1-ой странице тетради следует записать тему контрольной работы, номер варианта и номера задач.
4. Решение задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью выписать ее условие.
5. Решения задач нужно излагать подробно и аккуратно, объясняя все действия. В конце решения следует записать ответ.
|
|
|
Порядок защиты и ответственность студента за выполнение контрольной работы
Студент обязан предоставить решенную контрольную работу на рецензию преподавателю за 1 неделю до сессии.
Контрольная работа, выполненная не по своему варианту, не допускается к собеседованию. К собеседованию не допускается также работа, в которой выполнены не все задания.
После получения прорецензированной работы студент должен исправить в ней все отмеченные рецензентом ошибки и недочеты. С исправленной работой следует явиться на повторное собеседование, во время которого студент обязан ответить на два любых теоретических вопросов из списка. При положительном ответе на вопросы и верном исправлении решений студент получает зачет по контрольной работе.
Без зачета по контрольной работе студент не допускается к зачету или экзамену по данной дисциплине.
Контрольная работа.
Вопросы к экзамену (теоретические вопросы).
- Система действительных чисел и её свойства.
- Абсолютные величины и их свойства
- Ограниченные числовые множества. Точные границы множества
- Понятие действительные функции
- Элементарные функции и их классификация
- Числовая последовательность. Предел числовой последовательности
- Свойства пределов числовой последовательности.
- Ограниченные и монотонные последовательности.
- Свойства пределов, связанные с арифметическими операциями над последовательностями
- Число е. Лемма Бернулли.
- Критерий Коши сходимости последовательностей.
- Предел функции.
- Свойства пределов функции
- Первый замечательный предел.
- Бесконечно малые и бесконечно большие функции.
- Второй замечательный предел.
- Сравнение бесконечно малых и бесконечно больших функций.
- Непрерывность функции в точке.
- Свойства функций, непрерывных в точке.
- Свойства функций, непрерывных на отрезке [а;b].
- Непрерывность элементарных функций (многочлены и дробно-рациональные функции; степенные функции хn ,где n? Q, показательная функция, тригонометрические функции и обратные им).
- Понятие производной функции.
- Дифференциал функции.
- Геометрический смысл производной функции. Физический смысл производной функции.
- Дифференцирование сложной функции.
- Дифференцирование обратной функции.
- Инвариантность формы записи дифференциала.
- Арифметические операции над дифференцируемыми функциями.
- Дифференцирование элементарных функций.
- Производные высших порядков.
- Производные n-го порядка и их свойства.
- Дифференциалы высших порядков.
- Раскрытие неопределенностей по правилу Лопиталя.
- Сравнение роста степенной и показательной функций.
- Условие постоянства возрастания и убывания функции.
- Экстремум функции. Наибольшее и наименьшее значения.
- Направления выпуклости и вогнутости кривой и точки перегиба.
- Исследование функций и построение графиков.
|
|
|
Варианты контрольных заданий
I. Доказать, что
-
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,1.
не превосходит 0,1. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,1.
не превосходит 0,1. -
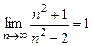 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,1.
не превосходит 0,1. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001. -
 . Начиная с какого n, величина не
. Начиная с какого n, величина не 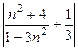 превосходит 0,001.
превосходит 0,001. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,1.
не превосходит 0,1. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,01.
не превосходит 0,01. -
 . Начиная с какого n, величина
. Начиная с какого n, величина  не превосходит 0,001.
не превосходит 0,001.
|
|
|
II. Вычислить предел последовательности:
1.  . 2.
. 2. 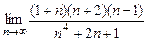 .
.
3.  . 4.
. 4.  .
.
5.  6.
6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10. 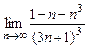
11.  12.
12. 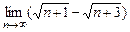
13.  14.
14. 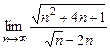
15.  16.
16. 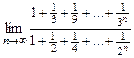
17.  18.
18. 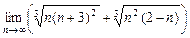
19.  20.
20. 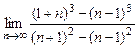
21.  22.
22. 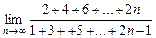
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 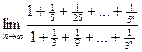
29.  30.
30. 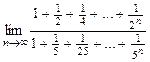
III. Вычислить предел функции:
1.  , ,
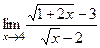 . .
| 2.  , ,
 . .
|
3.  , ,
 . .
| 4.  , ,
 . .
|
5.  , ,
 . .
| 6.  , ,

|
7.  , ,
 . .
| 8.  , ,

|
9.  , ,

| 10.  , ,

|
11.  , ,

| 12.  , ,
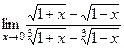 . .
|
13. 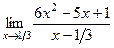 , ,
 . .
| 14.  , ,
 . .
|
15.  , ,
 . .
| 16.  , ,
 . .
|
17.  , ,
 . .
| 18.  , ,
 . .
|
19.  , ,

| 20.  , ,
 . .
|
21.  , ,
 . .
| 22.  , ,
 . .
|
23.  , ,

| 24.  , ,

|
25.  , ,
 . .
| 26.  , ,
 . .
|
27.  , ,
 . .
| 28.  , ,

|
29.  , ,

| 30.  , ,

|
IV. Вычислить предел функции
1.  ;
; 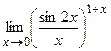
2.  ;
; 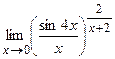
3.  ;
; 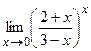
4.  ;
;  ;
;
5.  ;
; 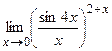
6.  ;
; 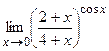
7.  ;
; 
8.  ;
; 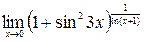
9. 
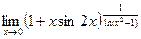
10. 
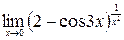
11. 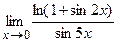
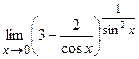
12. 
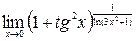
13. 
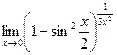
14. 
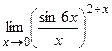
15. 
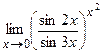
16. 
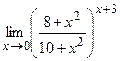
17. 
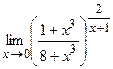
18. 
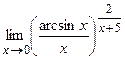
19. 
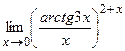
20. 
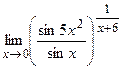
21. 

22. 

23. 
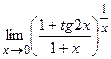
24. 
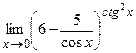
25. 

26. 
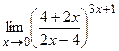
27. 

28. 
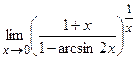
29. 
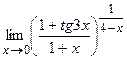
30. 
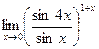
V.Найти производную функции

|
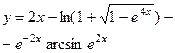
|

| ||||

|

|

| ||||

|

|

| ||||

|

|

| ||||

|

|

| ||||

|
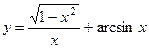
|

| ||||

|

|

| ||||

|

|

| ||||

|

|

| ||||

|

|

|
VI. Приложение производной
1.Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

| ||||
Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

| ||||
Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

|
Найти приближенное значение функции с помощью дифференциала:

| ||||
Найти приближенное значение функции с помощью дифференциала:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

|
Найти уравнение касательной к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

| ||||
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
Найти уравнение нормали к данной кривой в точке с абсциссой х о:

|
|
|
|
VII. Провести полное исследование функций и построить их графики:
 ; ;
 . .
|
 ; ;  . .
|
 ; ;
 . .
| ||||
 ; ; 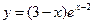 . .
|
 ; ;  . .
|
 ; ;
 . .
| ||||
 ; ;
 . .
|
 ; ;
 . .
|
 ; ;
 . .
| ||||
 ; ;
 . .
|
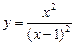 ; ;  . .
|
 ; ;  . .
| ||||
 ; ;
 . .
|
:
 ; ;  . .
|
 ; ;
 . .
| ||||
 ; ;
 . .
|
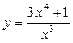 ; ;  . .
|
 ; ;
 . .
| ||||
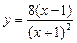 ; ;
 . .
|
 ; ;  . .
|
 ; ;
 . .
| ||||
 ; ;
 . .
|
 ; ;  . .
|
 ; ;  . .
| ||||
 ; ;
 . .
|
 ; ;  . .
|
 ; ;
 . .
| ||||
 ; ;  . .
|
 ; ;  . .
|
 ; ;  . .
|
Пример решения контрольной работы
1. Доказать, что 

Решение:
Используя определение предела числовой последовательности на языке «ε - δ»:  зададим произвольно сколь угодно малое число
зададим произвольно сколь угодно малое число  и покажем, что для него можно найти такое число
и покажем, что для него можно найти такое число  , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами  будет выполняться неравенство
будет выполняться неравенство
 (1)
(1)
Для отыскания числа  решим неравенство (1) относительно
решим неравенство (1) относительно  . Так как
. Так как  , то от этого неравенства переходим к следующему неравенству
, то от этого неравенства переходим к следующему неравенству
 Из последнего выражения следует, что за
Из последнего выражения следует, что за  можно принять число удовлетворяющее условию
можно принять число удовлетворяющее условию
 (2)
(2)
Таким образом, при произвольном  найдено число
найдено число  , такое, что для любого
, такое, что для любого  выполняет
выполняет
|
|
|


