 |
The technique of fiber optic low-coherence interferometry and its applications for fiber optic sensors.
|
|
|
|
Бурков В.Д., Потапов В.Т., Потапов Т.В., Удалов М.Е.
МЕТОДЫ ВОЛОКОННО-ОПТИЧЕСКОЙ НИЗКОКОГЕРЕНТНОЙ ИНТЕРФЕРОМЕТРИИ И ИХ ПРИМЕНЕНИЕ В РАЗРАБОТКАХ ВОЛОКОННО-ОПТИЧЕСКИХ ДАТЧИКОВ ФИЗИЧЕСКИХ ВЕЛИЧИН.
Приведен сравнительный анализ методов волоконно-оптической низкокогерентной когерентной интерферометрии для измерения малых расстояний и перемещений объектов в пространстве. Проанализирована возможность применения этих методов в разработках миниатюрных ВОД физических величин на основе микроинтерферометров Фабри-Перо.
Ключевые слова: волоконно-оптические датчики, низкокогерентная интерферометрия, микроинтерферометр Фабри-Перо.
Burkov V.D., V.T. Potapov V.T., T.V. Potapov T.V., Udalov M.E.
THE TECHNIQUE OF FIBER OPTIC LOW-COHERENCE INTERFEROMETRY AND ITS APPLICATIONS FOR FIBER OPTIC SENSORS.
Abstracts: the technique of fiber optic low-coherence interferometry for applications in the field fiber optic sensors in presented. The possibilities of use this technique for designing miniature fiber optic sensors are discussed.
Key words: fiber-optics sensors, low-coherence interferometry, microinterferometer Fabry-Perot.
В.Д. БУРКОВ, проф. МГУЛ, д. т. н., burkov@mgul.ac.ru
В.Т. ПОТАПОВ, проф. МГУЛ, д. т. н.,
Т.В. ПОТАПОВ, Фрязинский филиал Института радиотехники и электроники РАН, к. ф.–м. н.
М.Е. УДАЛОВ, доц. МГУЛ, к. т. н.
МЕТОДЫ ВОЛОКОННО-ОПТИЧЕСКОЙ НИЗКОКОГЕРЕНТНОЙ ИНТЕРФЕРОМЕТРИИ И ИХ ПРИМЕНЕНИЕ В РАЗРАБОТКАХ ВОЛОКОННО-ОПТИЧЕСКИХ ДАТЧИКОВ ФИЗИЧЕСКИХ ВЕЛИЧИН.
Значительная часть современных оптических датчиков физических величин основана на измерении оптического пути световых лучей и его изменений под влиянием внешних воздействий в заданном пространстве или объеме, т.е. на измерениях расстояний и перемещений, в которые конвертируются различные физические величины, такие, как давление, температура, магнитное поле [1,3,5,6], деформации [4] и т.д. К настоящему времени известно большое число оптических методов и схем измерения расстояний и перемещений различных объектов в пространстве. В последние годы благодаря освоению волоконно-оптических технологий получили развитие волоконно-оптические методы и устройства измерения расстояний и перемещений и, в частности, метод волоконно-оптической низкокогерентной интерферометрии (ВОНКИ) [4,2]. Основным отличием низкокогерентной интерферометрии от классической когерентной является применение низкокогернтных источников излучения, длина когерентности которых может быть меньше длины измеряемого оптического пути, например, суперлюминесцентных светодиодов. В когерентной или лазерной интерферометрии наоборот применяются высококогерентные источники – лазеры, имеющие длину когерентности намного превышающую длину измеряемого оптического пути. В случае когерентного источника излучения (лазера) зависимость интенсивности излучения от разности фаз  интерферирующих лучей на выходе интерферометра Фабри-Перо низкого контраста (прошедших или отраженных), когда значения коэффициентов отражения ИФП много меньше 1, носит строго периодический характер и описывается выражением
интерферирующих лучей на выходе интерферометра Фабри-Перо низкого контраста (прошедших или отраженных), когда значения коэффициентов отражения ИФП много меньше 1, носит строго периодический характер и описывается выражением
|
|
|
 , (1)
, (1)
где  - интенсивность на входе ИФП; V – константа, описывающая видность интерференционной кривой и зависящая от характеристики отражателей ИФП и расходимости лучей; n – коэффициент преломления среды; d – расстояние между отражателями; λ – длина волны света.
- интенсивность на входе ИФП; V – константа, описывающая видность интерференционной кривой и зависящая от характеристики отражателей ИФП и расходимости лучей; n – коэффициент преломления среды; d – расстояние между отражателями; λ – длина волны света.
Оптический путь (расстояния между зеркалами ИФП) можно определить путем подсчета интерференционных максимумов (или минимумов) на кривой, описываемой формулой (1) и расположенных на расстояниях равных  . Кроме этого для измерения перемещений необходимо определять еще и направление изменения оптического пути, что является непростой задачей и приводит к усложнению схемы. Точность измерений абсолютных расстояний таким методом составляет величину равную
. Кроме этого для измерения перемещений необходимо определять еще и направление изменения оптического пути, что является непростой задачей и приводит к усложнению схемы. Точность измерений абсолютных расстояний таким методом составляет величину равную  , а динамический диапазон может достигать значений 105 – 107. Однако при этом требуется применение дорогостоящего оборудования.
, а динамический диапазон может достигать значений 105 – 107. Однако при этом требуется применение дорогостоящего оборудования.
|
|
|
С лазерным интерферометром можно получить и значительно более высокую точность измерений, вплоть до нескольких нанометров при измерениях малых расстояний, соответствующих измерениям фаз в пределах  , т.е. при расстояниях
, т.е. при расстояниях  , где λ – длина волны света (λ
, где λ – длина волны света (λ  1 мкм; d ≤500 нм). Однако и при этом также приходится сильно усложнять схемы измерения, в частности, с высокой степенью стабилизировать рабочую точку интерферометра. Таким образом, когерентная лазерная интерферометрия позволяет получать более высокие точности измерений, но требует разработки сложного и дорогостоящего оборудования [4].
1 мкм; d ≤500 нм). Однако и при этом также приходится сильно усложнять схемы измерения, в частности, с высокой степенью стабилизировать рабочую точку интерферометра. Таким образом, когерентная лазерная интерферометрия позволяет получать более высокие точности измерений, но требует разработки сложного и дорогостоящего оборудования [4].
Одним из перспективных и практичных решений измерений абсолютных расстояний и перемещений, на наш взгляд, являются методы низкокогерентной волоконно-оптической интерферометрии (ВОНКИ), в которых применяются низкокогерентные источники, такие как лампы белого света и светодиоды [6,7]. Главными достоинствами ВОНКИ является достаточно высокая точность измерений, которая практически не зависит от флуктуаций оптической мощности в линии, дистанционность измерений и возможность создания миниатюрных чувствительных элементов ВОД. Методы ВОНКИ основаны на измерении автокорреляционной функции зондирующего излучения после его взаимодействия с образцом (чувствительным элементом, выполненным в виде ИФП). Эта автокорреляционная функция может быть измерена с помощью интерферометра с модулируемой разностью плеч – оптического коррелометра [5] или методом спектральной интерферометрии, который заключается в измерении спектра мощности излучения на выходе системы с последующей математической обработкой результатов.
В схемах с оптическим коррелометром возможны две конфигурации: тандемная и томографическая. В томографической конфигурации объект помещается внутрь оптического коррелометра и является его частью, такая схема, как следует из названия, реализуется в оптической когерентной томографии (ОКТ). Эта схема реализуется на основе интерферометра Майкельсона, одно из плеч которого образовано интерферометром Майкельсона с подвижным зеркалом, а в другом размещен исследуемый образец (рис. 1).
|
|
|
| Образец |
| СЛД |
| 3 dB |
| Подвижное зеркало |
| Фотодетектор |
Рис. 1. Оптическая схема томографического варианта
низкокогерентного интерферометра.
Когда разность оптических путей для двух разных плеч интерферометра становится близкой к длине когерентности источника излучения, на выходе схемы наблюдается интерференционная картина, которая изображена на рис. 2.
| I |
| φ |
Рис. 2. Изображение интерференционной картины интерферометра.
Для источника с гауссовым распределением интенсивности излучения по длинам волн (например, для суперлюминисцентного диода СЛД) интенсивность оптического сигнала на выходе оптического коррелометра (на входе фотодиода) имеет вид:
 , (2)
, (2)
где φ – это разность фаз двух лучей, Lc – длина когерентности источника.
Когда разность фаз равна нулю, эта функция имеет максимум. Таким образом, изменяя разность фаз с помощью подвижного зеркала интерферометра, можно установить момент, когда функция I максимальна, и отсюда определить фазовую задержку в образце [2, 5] и по её значению вычислить длину оптического пути света в образце. Если за время измерения длины одного из плеч интерферометра успевает измениться на некоторую величину, то изменяется и разность фаз, поэтому исследуемая величина измеряется с ошибкой, то же происходит при изменении температуры или вибрации. Таким образом, томографическая конфигурация не устойчива по отношению к изменениям внешних условий, что ограничивает область ее применения.
Лучшей помехоустойчивостью обладает схема, приведённая на рис. 3, в которой чувствительный и сканирующий интерферометры разделены и располагаются последовательно – тандемный вариант.
| Сканирующий (опорный) интерферометр - коррелометр |
| Р- внешнее воздействие |
| Делительная призма |
| Волоконный ответвитель |
| Широкополосный оптический источник |
| Чувствительный интерферометр Фабри-Перо |
  |
|
|
|
Рис. 3. Схема тандемного низкокогерентного интерферометра.
В этой схеме излучение широкополосного источника через одно из плеч волоконного разветвителя подается в чувствительный элемент (например, ИФП), а затем отраженный сигнал через другое плечо разветвителя поступает в сканирующий интерферометр с изменяющейся по линейному закону длиной оптического пути одного из плеч, характеристики которого должны быть жестко застабилизированы от внешних воздействий и возмущений. Разность хода лучей в двух плечах сканирующего интерферометра значительно превышает длину когерентности источника, поэтому интерференция от каждого интерферометра (измерительного и опорного) по отдельности не может наблюдаться. Если же оптическую разность хода сканирующего интерферометра, сделать достаточно близкой (в пределах длины когерентности источника) к разности хода в чувствительном интерферометре, то возникает интерференция лучей, поступающих на фотоприемник от двух интерферометров. Фаза и видность пичков интерференционной картины является функцией отличия разностей оптических путей (разностей фаз) двух интерферометров.
Функция пропускания такой системы имеет вид:
 , (3)
, (3)
где φ – разность фаз в чувствительном интерферометре, а φs – разность фаз в сканирующем интерферометре. По мере изменения разности фаз в сканирующем интерферометре, интенсивность на выходе такой тандемной системы изменяется согласно рис. 4.
| I |
| φ |
| Lc |
| φ-φs |
Рис. 4. Схематическое изображение функции пропускания тандемного низкокогерентного интерферометра
Функция пропускания максимальна в том случае, если φ=φs, таким образом, определяя максимум этой функции, мы определяем разность фаз в сканирующем интерферометре, а следовательно, и разность фаз в чувствительном интерферометре. Важно обратить внимание, что картина интерференции может наблюдаться, только если разность фаз чувствительного и сканирующего интерферометров не превышают длину когерентности источника излучения. При изменении разности фаз в чувствительном интерферометре, т.е. при изменении величины измеряемого внешнего параметра, максимум функции пропускания смещается; настраивая сканирующий интерферометр на этот максимум, можно вновь определить величину измеряемого параметра по изменению фаз. Следует отметить, что варианты метода ВОНКИ с оптическим коррелометром довольно сложны и дороги для практической реализации ВОД на их основе вследствие сложности их схем, требующих жесткой стабилизации параметров коррелометра.
|
|
|
Спектральный метод ВОНКИ
На наш взгляд, для практической реализации в настоящее время наиболее подходящим является метод спектральной ВОНКИ, т.к. он наиболее прост и дешев в реализации. Однако до сих пор остается неясным вопрос о точности измерений, которая может быть достигнута этим методом. Спектральный метод ВОНКИ заключается в измерении спектра мощности излучения образца (автокорреляционной функции зондирующего излучения после его взаимодействия с образцом) с последующей математической обработкой этого спектра. На рис. 5 приведена схема установки, реализующей спектральный метод ВОНКИ [1]. Здесь в качестве чувствительного элемента (образца) применяется интерферометр Фабри-Перо слабого контраста, образуемый, с одной стороны, торцoм оптического волокна, а с другой – какой-либо отражающей поверхностью, например, мембраной или торцом другого оптического волокна. Установка состоит из источника излучения, волоконно-оптической линии с разветвителем и спектрометра, включающего в себя отражательную дифракционную решетку (эшелет), объектив и ПЗС матрицу. Излучение широкополосного источника суперлюминесцентного светодиода SLD471, излучающего в диапазоне ~920-960 нм с центром на длине λ ≈940 нм по оптическому волокну попадает на ИФП, образованный на торце волокна. Отраженный от ИФП сигнал через разветвитель подается на вход спектрометра. Спектрометр выполнен по автоколлимационной схеме, свет проходит через объектив дважды - туда и обратно, при этом отраженный от решетки спектр излучения первого порядка регистрируется ПЗС матрицей с числом пикселей 640×512. Фокусное расстояние объектива составляет 50 мм, светосила 2,8,
| Широкополосный оптический источник |
| Дифракционная решетка |
| Разветвитель 2х2 |
| ПЗС матрица |
| Компьютер |
| Объектив |
| ИФП |
Рис. 5. Схема установки для измерения базы ИФП и перемещений.
диаметр аберрационного пятна  20 мкм. Дифракционная решетка представляет собой реплику на стекле, покрытую металлом. Размеры решетки 40×40 мм, число штрихов 600 шт/мм. Эффективность решетки в первом порядке дифракции составляет
20 мкм. Дифракционная решетка представляет собой реплику на стекле, покрытую металлом. Размеры решетки 40×40 мм, число штрихов 600 шт/мм. Эффективность решетки в первом порядке дифракции составляет  70%.
70%.
Известно [3,4], что спектр SLD имеет гауссово распределение в данном случае с центром на 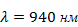 . Поэтому интенсивность отраженного сигнала будет представлять собой произведение функций отражения интерферометра Фабри-Перо слабого контраста (коэффициент отражения на границе кварц-воздух равен 0,04) и гауссовой функции источника, т.е. имеет вид:
. Поэтому интенсивность отраженного сигнала будет представлять собой произведение функций отражения интерферометра Фабри-Перо слабого контраста (коэффициент отражения на границе кварц-воздух равен 0,04) и гауссовой функции источника, т.е. имеет вид:
 , (4)
, (4)
где  – мощность излучения на входе волоконного тракта;
– мощность излучения на входе волоконного тракта;  - константа, зависящая от величины потерь излучения и эффективности связи между ИФП и оптическим волокном, которые в условиях эксперимента можно считать постоянным;
- константа, зависящая от величины потерь излучения и эффективности связи между ИФП и оптическим волокном, которые в условиях эксперимента можно считать постоянным;  – коэффициент отражения от отражателей ИФП;
– коэффициент отражения от отражателей ИФП;  – коэффициент преломления среды (для воздуха
– коэффициент преломления среды (для воздуха  )
)
На рис. 6 в качестве иллюстрации приведен спектр отраженного сигнала от ИФП, образованного торцами двух оптических волокон, расположенных на расстоянии  .
.

Рис. 6. Спектр интерферометра Фабри-Перо
Из формулы (4) следует, что максимумы в спектре отражения при фиксированном значении  находятся один от другого на расстояниях, определяемых из условия разности фаз, равной
находятся один от другого на расстояниях, определяемых из условия разности фаз, равной  :
:
 . (5)
. (5)
Отсюда выражение для базы ИФП  имеет вид:
имеет вид:
 при
при  =1. (6)
=1. (6)
Таким образом, для вычисления  необходимо определить длины волн, на которых располагаются (или минимумы) спектра отражения ИФП
необходимо определить длины волн, на которых располагаются (или минимумы) спектра отражения ИФП
Точность измерения  в этом случае будет определяться точностью измерения
в этом случае будет определяться точностью измерения  , т.е. спектральными характеристиками прибора, в том числе характеристиками ПЗС матрицы и отношением сигнал/шум [8]. В настоящее время существующие спектральные приборы на основе дифракционных решеток позволяют измерять спектры излучения в ближней ИК области с разрешением в сотые доли нанометров. В этом случае, как показывают оценки, точность измерения расстояний методом ВОНКИ может достигать 10 нм в диапазоне расстояний от 50 до 250 мкм. Тогда на базе описанного выше метода ВОНКИ возможно создание высокоточных датчиков для измерения абсолютных расстояний с динамическим диапазоном ≃104. В данном макете устройства точность измерений ограничивалась шумами ПЗС-матрицы и составляла примерно ±100 нм при измерении расстояния между торцами оптических волокон в пределах 100 мкм.
, т.е. спектральными характеристиками прибора, в том числе характеристиками ПЗС матрицы и отношением сигнал/шум [8]. В настоящее время существующие спектральные приборы на основе дифракционных решеток позволяют измерять спектры излучения в ближней ИК области с разрешением в сотые доли нанометров. В этом случае, как показывают оценки, точность измерения расстояний методом ВОНКИ может достигать 10 нм в диапазоне расстояний от 50 до 250 мкм. Тогда на базе описанного выше метода ВОНКИ возможно создание высокоточных датчиков для измерения абсолютных расстояний с динамическим диапазоном ≃104. В данном макете устройства точность измерений ограничивалась шумами ПЗС-матрицы и составляла примерно ±100 нм при измерении расстояния между торцами оптических волокон в пределах 100 мкм.
Библиографический список
1. В.Д. Бурков, В.Т. Потапов, Т.В. Потапов, М.Е. Удалов, «Волоконно-оптические датчики физических величин на основе низкокогерентной интерферометрии», Вестник Московского государственного университета леса: «Лесной вестник» №5(74) 2010 г., стр. 157-161.
2. Bing Yu, Dae Woong Kim, Jiang Deng, Hai Xiao and Anbo Wang, “Fiber Fabry-Perot senses for detection of partial discharges in power transformers”, Appl.optics, vol.42, №16, 2003.
3. Y.J.Rao and D.Jackson, “Recent progress in fiber optic low-coherence interferometry”, Meas.Sci.Technol., 1996, pp. 981-989.
4. Patricia M. Hieva, “New trends on MEMS sensor technology for harsh environmental applications”, Sensors And Transducers Journal, Special Issue, Oct. 2007, pp.10-30 (имеется русский перевод в журнале «Датчики и системы», №5, 2008 г., стр. 38-46, «Новые тенденции в технологии MEMS-датчиков для применения в жестких условиях»).
5. Ki D. Oh, J. Ranade, V. Arya, A. Wang, R.O. Claus “Miniaturized fiber optic magnetic field sensors”, SPIE, v.3538, pp.136-142, 1998.
6. В.В.Иванов, В.А.Маркелов, М.А.Новиков, С.С.Уставщиков, «Дифференциальная низкокогерентная интерферометрия для in situ диагностики прозрачных микроструктур», Письма в ЖТФ, 2004 г., т.30, выпуск 9, стр.82-87.
7. S.Taplin, A.Gh.Podoleanu, D.J.Webb and D.A.Jackson, “Displacement Sensor Using Channeled Spectrum Dispersed on a Linear CCD Array”, Electron.Lett., v.29, pp.893, 1993.
8. A.Gh.Podoleanu, S.Taplin, D.J.Webb and D.A.Jackson, “Channelled Spectrum Liquid Refractometer”, Rev. Sci. Instr., vol. 64, No.10, pp. 3028-9, 1993.
|
|
|


