Основные логические законы.

Главная | Обратная связь | Поможем написать вашу работу!

(А Ù В) Ú ( Ù )

Элементы математической логики.

Высказывания и операции над ними.

Определение. Высказывание – повествовательное предложение (утвержде-ние, суждение), о котором имеет смысл говорить, что оно истинно или ложно. Истинность принимается за 1, ложь за 0.

Пример. Обозначим высказывания p,q. p=0 означает, что p – ложное высказывание.

Определение. Математическая логика - наука, изучающая методы установления истинности или ложности высказываний.

Из одних высказываний можно формировать другие.

Определение. Будем называть высказывание простым (элементарным), если оно рассматривается нами как некое неделимое целое (аналогично элементу множества). Сложным (составным) называется высказывание, составленное из простых с помощью логических связок (логических операций).

Каждое высказывание может быть истинным или ложным, результат операции с высказываниями также может быть ложным или истинным. Операции над высказываниями удобно представлять с помощью таблиц истинности.

Операция	Обозначение	Определение истинности результата	Таблица истинности
Отрицание	(┐ p) (не р)	Отрицание истинно, если высказывание ложно и наоборот
Конъюнкция – логическое произведение	p ^ q p «и» q	Конъюнкция истинна тогда и только тогда, когда истинны оба высказывания
Дизъюнкция – логическая сумма	p V q p «или» q	Дизъюнкция истинна тогда и только тогда, когда истинно хотя бы одно высказывание
Импликация – логическое следование	p ® q (p É q) (из р следует q) (если р, то q)	Импликация ложна тогда и только тогда, когда условие истинно, а заключение ложно
Эквивален-ция – логическое равенство	p «q (p~ q) p º q р эквивалентно q	Эквиваленция истинна тогда и только тогда, когда высказывания при-нимают одинако-вое значение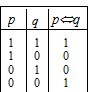

Пример 1. Высказывание «идет дождь или снег» истинно тогда, когда выполняется хотя бы одна его часть.

Пример 2. Высказывание «идет дождь и снег» истинно тогда, когда выполняются обе его части.

Логика высказываний - раздел логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения. Внутренняя структура простых высказываний не рассматривается, а учитывается лишь, с помощью каких связок и в каком порядке простые высказывания соединяются в сложные.

Буквы, обозначающие высказывания, логические связки и скобки, составляют алфавит языка логики высказываний.

Логические формулы.

С помощью элементов алфавита из произвольных высказываний последовательным применением логических операций могут быть образованы новые высказывания сколь угодно сложного вида. Такие высказывания называются логическими формулами.

Определение. Выражение, составленное из обозначений высказываний, связок и скобок, назовем логической формулой, если оно удовлетворяет следующим условиям:

· любая переменная, обозначающая высказывание, – формула;

· если А и В – формулы, то (А Ù В), (А Ú В), , (А ® В), (А «В) – формулы;

· других формул нет.

С помощью формул логики высказываний можно описать и исследовать структуру сложных высказываний, установить их истинность или ложность в зависимости от истинности или ложности входящих в нее простых высказываний. Язык логики применяется также для записи математических определений и теорем.

Пример. Пусть А,В,С – высказывания. Тогда формулами будут:

А®В (А®В) Ù С (АÙС)®(ВÚА) ù (ВÚА) (ВÚА)Ù(СÚА)

Если логическое выражение не содержит скобок, то приоритет выполнения логических операций таков:

1. Выражение в скобках

2. ù (НЕ)

3. Ù (И)

4. Ú (ИЛИ)

5. ®

6. «

Пример. Расставьте скобки:

А ® В Ú С С «А Ù В ® Ú С
А ® (В Ú С) С «(А Ù В) ® ( Ú С). – 1 шаг

С «((А Ù В) ® ( Ú С)). – 2 шаг

Пример. Представить логическими формулами следующие высказывания:

«Если идет дождь, то на асфальте лужи. Дождя нет, а лужи есть».

Обозначим: А=«идет дождь». В= «на асфальте лужи». Тогда наше высказывание запишется так: (А->В)^ (┐А^ В)

Если задана логическая формула с некоторыми переменными, то значение формулы удобно вычислять с помощью таблиц истинности..

Пример. Определить, когда формула (А Ù В) Ú ( Ù ) принимает значения истина, а когда ложь.

Определение. Логические формулы называются равносильными, если при всех истинностных значениях переменных они одноврем. истинны или ложны.

Пример 6. Доказать равносильность формул: А ® B Û Ú B;

Если из А следует В, это означает то же, что выполняются или неА, или В

А	В	А®В	ÚВ

В произвольных высказываниях мы можем заменять их части на равносильные им выражения, часто это позволяет упростить исходные высказывания.

Основные логические законы.

Приведем некоторые важные (в том числе для приложений к высказываниям естественного языка) логические законы.

Законы для операций и, или (остальные операции могут быть выражены через и, или):

операции	коммутативность	ассоциативность	дистрибутивность
Конъюнкция	p Ù q º q Ù p	(p Ù q)Ù r º p Ù(q Ù r)	(p Ú q)Ù r º (p Ù r)Ú (q Ù r)
Дизъюнкция	p Ú q º q Ú p	(p Ú q)Ú r º p Ú(q Ú r)	(p Ù q)Ú r º (p Ú r)Ù(q Ú r)

Закон тождества	АºА	всякая мысль в процессе рассуждения должна быть тождественна самой себе
Закон непротиворечия	А Ù º 0	два несовместимых друг с другом суждения не могут быть одновременно истинными
Закон исключения третьего	А Ú º 1	два противоречащих суждения не могут быть одновременно ложными, одно из них необходимо истинно
Законы поглощения	0Ú q = q, 1 Ù q = q
Законы нуля и единицы	1Ú q = 1, 0 Ù q = 0
Законы идемпотентности	AÚ A= A, АÙА=А
	AÚ =1 AÙ =0
Законы двойственности (законы де Моргана):	º Ù º Ú	Если не выполняется «или А или В», следовательно, имеют место и не А, и не В.
Закон двойного отрицания	º р	Отрицание отрицания есть утверждение.

Также полезными являются следующие тождества:

· А ® B Û Ú B; (мы его доказали)

· А ® B Û -> .

Пример 7.

· Отрицание высказывания «идет дождь или идет снег», равносильно выполнению двух высказываний: «нет дождя» и «нет снега».

· Отрицание отрицания: не «нет дождя» означает, что «дождь есть».

12 Следующая ⇒

Воспользуйтесь поиском по сайту: