 |
к лабораторной работе № И1
|
|
|
|
ИНТЕРФЕРЕНЦИЯ СВЕТА
Лабораторная работа № И1
Изучение интерференционного опыта Юнга
С помощью лазера
Цель работы: наблюдение интерференционной картины от двух отверстий, освещенных лазером, и определение расстояния между ними.
Оборудование: гелий-неоновый лазер, пластинка с двумя отверстиями, экран, линза, линейка.
Краткие теоретические сведения
Явление интерференции света осуществляется при наложении когерентных световых волн от двух точечных источников света S 1 и S 2, находящихся на расстоянии d друг от друга (рис. 1).

Рис. 1
В некоторой точке пространства М происходит усиление или ослабление света в зависимости от величины разности хода между интерферирующими лучами света: D = r2 – r1.
Максимальное усиление света наблюдается в тех точках пространства, для которых разность хода световых лучей D равна целому числу длин волн или четному числу полуволн:
 (
( = 0, 1, 2, 3,... – порядок интерференции).
= 0, 1, 2, 3,... – порядок интерференции).
Минимум интенсивности при ослаблении света наблюдается при условии, если разность хода D равна полуцелому числу длин волн или нечетному числу полуволн
 (
( = 0, 1, 2, 3,....).
= 0, 1, 2, 3,....).
В целом интерференционная картина представляет собой систему чередующихся светлых и темных полос в некоторой плоскости Р, находящейся на расстоянии r от источников S 1 и S 2 (см. рис. 1). Когда расстояние r намного превосходит расстояние d между источниками света (при r >> d), можно считать, что
 ,
,  ,
,
где y – координата, определяющая положение интерференционной полосы относительно центра О интерференционной картины, что следует из подобия треугольников S 1 BS 2 и МСО. В этом случае положение светлых и темных полос в положительном и отрицательном направлении оси y будет определяться формулой
|
|
|

За ширину интерференционной полосы принимают расстояние между центрами двух соседних светлых или темных полос:
D y = y m – y m-1 =  .
.
В данной работе ставится задача нахождения расстояния между источниками света S1 и S2:
 =
=  . (1)
. (1)
Описание установки
В опыте Юнга в качестве источников света S 1 и S 2 используются два отверстия в пластинке, помещаемой на пути лазерного луча. Поскольку лазерное излучение обладает большой пространственной когерентностью по всему поперечному сечению светового пучка, отверстия S 1 и S 2 представляют собой когерентные источники света, что является необходимым условием осуществления интерференции света. Для нахождения расстояния d между источниками, согласно (1), необходимо знать длину волны l лазерного излучения, расстояние r от отверстий до плоскости Р и ширину интерференционных полос. Непосредственные измерения D y практически невозможны из-за мелкого масштаба наблюдаемой интерференционной картины. Поэтому между лазером и экраном помещают линзу L, дающую увеличенное изображение интерференционных полос на экране Э (рис. 2).
На рисунке D y ' соответствует увеличенному изображению ширины D y интерференционной полосы, равной расстоянию между центрами соседних светлых полос нулевого (m = 0) и первого (m = 1) порядков.
Из подобия треугольников АМО и А'M'O следует:
 . (2)
. (2)

Рис. 2
Расстояние  от плоскости Р до линзы L можно найти по формуле линзы:
от плоскости Р до линзы L можно найти по формуле линзы:
 ,
,
где F – фокусное расстояние линзы. Тогда
 .
.
Подставив это выражение в (2), получим
|
|
|
 .
.
Учитывая, что

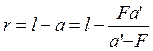 ,
,
и подставляя выражение, полученное для D y, в (1), получим формулу для вычисления расстояния между источниками света S 1 и S 2:
d =  . (3)
. (3)
Расстояние l от пластины с отверстиями до линзы, ширину наблюдаемой интерференционной полосы D y ' и расстояние а ' от линзы до экрана Э измеряют с помощью линейки. Фокусное расстояние линз F указывается на установке. Длина волны излучения гелий-неонового лазера l = 632,8 нм.
Порядок выполнения работы
1. Включить лазер и направить луч на экран.
2. Поставить на пути луча пластинку с отверстиями. На экране появится интерференционная картина.
3. Поместить между пластинкой с отверстиями и экраном линзу с известным фокусным расстоянием F для получения увеличенного изображения интерференционных полос.
4. Измерить ширину D y ' интерференционных полос, полученных на экране. Для этого, положив лист бумаги на экран, отметить карандашом середины темных полос, измерить ширину нескольких полос и разделить ее на число полос.
5. Измерить расстояние l и а '.
6. Вычислить расстояние d по расчетной формуле (3).
7. Измерения провести для трех различных положений линзы.
8. Определить среднее значение
< d > =  .
.
9. Результаты измерений и вычислений занести в таблицу.
10. Оценить абсолютную и относительную погрешности измерений по формулам:
 ,
,
e = 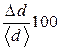 %.
%.
Таблица
| № | li,м | ai ', м | Δ yi',м | di, м | < d >,м | | di –< d >|, м | Δ d,м | ε, % |
| 1 |
|
|
| |||||
| 2 | ||||||||
| 3 | ||||||||
| λ = 632,8 нм | F = | |||||||
Контрольные вопросы
1. Что такое интерференция света? Каковы условия ее осуществления?
2. Получить выражение для ширины интерференционных полос в опыте Юнга.
3. Почему в центре интерференционной картины в опыте Юнга наблюдается светлая полоса?
4. Как осуществить опыт Юнга от обычной лампочки накаливания, являющейся некогерентным источником света?
5. С какой целью используется линза в данной работе?
|
|
|
6. Получить условия максимума и минимума интенсивности света в опыте Юнга.
7. Вывести формулу для определения расстояния между источниками света в опыте Юнга.
Библиографический список
к лабораторной работе № И1
1. Савельев, И. В. Курс общей физики / И. В. Савельев. – М., 1978. –
Т. 2. – § 119.
2. Зисман, Г. А. Курс общей физики / Г. А. Зисман, О. М. Тодес. –
М., 1972. – Т.3. – § 11.
3. Детлаф, А. А. Курс общей физики / А. А. Детлаф, Б. М. Яворский. – М., 1979. – Т. 3. – § 5.2.
|
|
|


