 |
Краткие теоретические сведения
|
|
|
|
ПОЛЯРИЗАЦИЯ СВЕТА
Лабораторная работа № П1
ИЗУЧЕНИЕ СВОЙСТВ ПЛОСКОПОЛЯРИЗОВАННОГО СВЕТА
Цель работы: проверка законов Малюса и Брюстера.
Оборудование: гелий-неоновый лазер или лампа накаливания, поляризатор в поворотной оправе, фотосопротивление, блок питания с микроамперметром, пластина диэлектрика на вращающемся лимбе, металлическая пластина.
Краткие теоретические сведения
Закон Малюса. Пусть плоскополяризованный свет с амплитудой колебаний электрического вектора ` Е P и интенсивностью Iр, полученный от лазера или пропусканием естественного света через поляризатор П (рис. 1, а), падает на анализатор А.
Предположим, что плоскость колебаний вектора ` Е П поляризованного света составляет угол j с плоскостью АА анализатора. Через анализатор пройдет только составляющая ` Е А, параллельная плоскости АА анализатора (рис. 1, б) и равная
 . (1)
. (1)
Перпендикулярную составляющую ` Е ^ анализатор не пропустит. Так как интенсивность света I пропорциональна квадрату амплитуды колебаний вектора 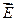 (I ~ E
(I ~ E  ), то, возведя левую и правую части соотношения (1) в квадрат, получим
), то, возведя левую и правую части соотношения (1) в квадрат, получим
 . (2)
. (2)
Таким образом, интенсивность света, прошедшего через анализатор I A, равна произведению интенсивности света, прошедшего через поляризатор I P, на квадрат косинуса угла j между плоскостью колебаний поляризованного света и плоскостью анализатора. Соотношение (2) называется законом Малюса. Согласно закону при вращении анализатора вокруг луча интенсивность поляризованного света I А, проходящего через анализатор, будет меняться от I min = 0 (при j = p/2) до I max = I П (при j = 0).
|
|
|

Рис. 1
Закон Брюстера. При падении естественного света на границу раздела двух изотропных диэлектриков отраженный и преломленный лучи света частично поляризуются. При угле падения aБ, удовлетворяющему условию
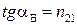 , (3)
, (3)
(n 21 – показатель преломления второй среды относительно первой, n 21= n 2 / n 1), отраженный свет полностью поляризуется. В нем содержатся только колебания светового вектора ` Е, перпендикулярные плоскости падения (точки на рис. 2). При этом преломленный луч поляризован лишь частично с преобладанием колебаний вектора ` Е, лежащих в плоскости падения (стрелки на рис. 2). Соотношение (3) называется законом Брюстера, а угол aБ – углом Брюстера или углом полной поляризации. Он имеет определенное значение для каждого диэлектрика. При выполнении условия (3) отраженный луч перпендикулярен преломленному (ОВ  ОС на рис. 2, а).
ОС на рис. 2, а).
Можно дать следующее физическое истолкование закона Брюстера. Падающий на границу раздела двух диэлектриков естественный свет можно представить в виде двух плоскополяризованных некогерентных волн с векторами  , находящимися во взаимно перпендикулярных плоскостях. Пусть одна из компонент вектора
, находящимися во взаимно перпендикулярных плоскостях. Пусть одна из компонент вектора  лежит в плоскости падения (стрелки на луче АО, рис. 2), а другая перпендикулярна плоскости падения (точки на луче АО, рис. 2, а).
лежит в плоскости падения (стрелки на луче АО, рис. 2), а другая перпендикулярна плоскости падения (точки на луче АО, рис. 2, а).

Рис. 2
При проникновении световой волны в диэлектрик ее электрический вектор ` Е вызывает вынужденные колебания электронов, принадлежащих атомам (или молекулам) второй среды. Колебания электронов совершаются
в направлениях, совпадающих с направлениями вектора ` Е, т. е. в плоскости падения и перпендикулярно ей. Колеблющийся электрон излучает вторичную электромагнитную плоскополяризованную волну, интенсивность I которой зависит от направления её распространения и может быть представлена полярной диаграммой излучения (рис. 3).
|
|
|

Рис. 3
Здесь радиус-вектор ` r характеризует величину интенсивности излучения в определенном направлении. Как видно из диаграммы, вдоль оси колебания электрона y излучение отсутствует, а вдоль направления x, перпендикулярного этой оси, интенсивность излучения максимальна. Поскольку при падении света на диэлектрик под углом Брюстера отраженный луч ОВ перпендикулярен преломленному ОС (рис.2), то ОВ совпадает с направлением колебаний вектора `Е и направлением колебаний электронов, колеблющихся в плоскости падения, и, следовательно, эти электроны не излучают энергии вдоль ОВ на рис. 2, совпадающей с осью у на рис. 3.
Таким образом, в отраженной волне отсутствуют колебания электрических векторов ` Е в плоскости падения и содержатся только перпендикулярные ей. Однако эксперимент показывает, что закон Брюстера соблюдается не строго. Например, коэффициент отражения плоскополяризованного света с колебаниями ` Е в плоскости падения не обращается в нуль ни для какого угла падения, хотя при угле Брюстера он и очень мал. Такое отступление от точного выполнения закона Брюстера можно объяснить наличием на поверхности тонкого переходного слоя, свойства которого отличны от свойств самой среды. Некоторые возможные причины возникновения таких переходных слоев следующие:
1) электрическое поле световой волны, действующее на приграничные молекулы среды, может отличаться от действующего поля для остальных молекул;
2) анизотропные молекулы, если среда построена из таковых, могут ориентироваться вблизи поверхности в некоторых преимущественных направлениях;
3) плотность среды в таком приграничном слое может отличаться от плотности остальной среды.
Описание установки
Установка для проверки закона Малюса состоит из источника поляризованного света – лазера 1, анализатора 2 и фотосопротивления 3, установленных по схеме, изображенной на рис. 4. Вместо лазера можно использовать лампу накаливания и поляризатор.
|
|
|

Рис. 4
Анализатор снабжен поворотным вращающимся лимбом, по которому отсчитываются углы поворота плоскости анализатора. Фотосопротивление преобразует падающий на него свет в фототок, пропорциональный интенсивности падающего света. Фототок измеряется микроамперметром.
Установка для проверки закона Брюстера содержит источник поляризованного света – лазер (или лампу накаливания с поляризатором) и пластинку диэлектрика (стекло). Пластинка укреплена на горизонтальном поворотном диске с лимбом для отсчета углов и может вращаться вокруг вертикальной оси. За отраженным лучом наблюдают по экрану или на стене.
Порядок выполнения работы
Задание 1. Проверка закона Малюса
1. Тумблером включите лазер согласно инструкции. Не смотрите на встречу лазерному лучу!
2. Включите питание фотосопротивления.
3. Установите анализатор и фотосопротивление так, чтобы световой луч, пройдя через центр анализатора, попадал на фотосопротивление.
4. Вращая анализатор, найдите такое его положение, при котором фототок (показания микроамперметра) имеет максимальное значение i max. При этом деление на лимбе анализатора берется за начало отсчета угла j и принимается равным нулю.
5. Поверните анализатор на 10° и запишите показания микроамперметра в табл. 1.
Таблица 1
| Номер измерения | j, град | i, мкА | cos2j |
| 1 .. 36 |
6. Измерения проведите до 360° через каждые 10°.
7. Выключите питание фотосопротивления и лазер.
8. По экспериментальным точкам (табл. 1) постройте график зависимости фототока i, пропорционального интенсивности I проходящего через анализатор света, от квадрата косинуса угла поворота анализатора I = f (cos2j). Сравните график с теоретической зависимостью по закону Малюса.
Задание 2. Проверка закона Брюстера
1. Уберите анализатор и фотосопротивление с оптической скамьи.
2. Установите пластинку диэлектрика на диске с лимбом так, чтобы отраженный луч попадал в выходное отверстие лазера. Угол падения луча при этом равен 0°.
|
|
|
3. Медленно поворачивая диск с диэлектриком, увеличивайте угол падения и наблюдайте на экране (стене) за изменением интенсивности отраженного луча. Так как плоскость колебания вектора ` Е в падающем луче совпадает с плоскостью падения луча, то при угле его падения, равном углу Брюстера, отраженный луч будет иметь минимальную интенсивность. Найдите такое положение пластинки диэлектрика и запишите значение угла Брюстера в табл. 2 (рис. 2).
Таблица 2
| Номер измерения | aБ, град | <aБ>, град | < n > |
| 1 × × 5 |
4. Измерения повторите пять раз.
5. По среднему значению угла Брюстера найдите показатель преломления диэлектрической пластины.
6. Оцените ошибку измерений и результат запишите в следующем виде: n = < n > ± D n
7. Замените пластину диэлектрика металлической и оцените характер поляризации отраженного от металла света.
Контрольные вопросы
1. Что представляет собой свет с точки зрения электромагнитной теории?
2. Какой свет называется плоскополяризованным и чем он отличается от естественного света?
3. Что такое плоскость поляризации (плоскость колебаний) светового луча?
4. Вывести и пояснить закон Малюса.
5. Поясните схему установки, на которой проверяется закон Малюса. Проанализируйте полученные результаты. Выполняется ли закон Малюса?
6. В чем заключается закон Брюстера?
7. Почему свет, отраженный от диэлектрика под углом Брюстера, является плоскополяризованным?
8. Объясните наблюдаемое в опыте изменение интенсивности отраженного от диэлектрика луча света.
9. Расскажите об устройствах для получения плоскополяризованного света.
10. Где применяется поляризованный свет?
Библиографический список
|
|
|


