Краткие теоретические сведения

Лабораторная работа № П2

 

ПОВОРОТ  ПЛОСКОСТИ  ПОЛЯРИЗАЦИИ  СВЕТА  В  МАГНЕТИКЕ

Цель работы: ознакомиться с основанным на эффекте Фарадея магнитооптическим методом наблюдения доменной структуры, вычислить постоянную Верде (V) для ферримагнетика, проверить закон Малюса.

Оборудование: микроскоп, поляризатор, анализатор, образец прозрачного ферримагнетика, источник света.

 

Краткие теоретические сведения

 

Вещества, способные вращать плоскость поляризации, называются оптически активными. Некоторые вещества становятся оптически активными в магнитном поле.

Впервые вращение плоскости поляризации при прохождении света через вещество, находящееся в магнитном поле, наблюдал Фарадей в 1846 году, поэтому это явление называется эффектом Фарадея. В магнитоупорядоченных веществах (ферромагнетиках, антиферромагнетиках, ферримагнетиках) угол поворота плоскости поляризации

 

j = V × l × J_s,                                              (1)

 

где V – коэффициент пропорциональности, зависящий от свойства вещества, температуры, частоты (длины волны) света, называющийся постоянной Верде; l – путь света в веществе; J_s – намагниченность вещества.

Направление вращения плоскости поляризации зависит от направления магнитного поля, направления вектора намагниченности и направления распространения света.

В магнитоупорядоченных веществах имеются области самопроизвольной намагниченности до насыщения J_s, которые называются доменами. Несмотря на это, без внешнего магнитного поля магнетики находятся в размагниченном состоянии, то есть проекция магнитного момента всего образца на любое направление равна нулю.

В магнетиках с одноосной анизотропией имеется направление, называемое осью легкого намагничивания, вдоль которого выстраиваются магнитные моменты в доменах. В этом случае энергия (магнитного происхождения) всего образца будет минимальной и магнетики будут находиться в устойчивых равновесных состояниях.

Доменная структура для тонкого образца (пленки с подложкой) из феррита-граната (ферримагнетики) с осью легкого намагничивания, направленной перпендикулярно плоскости образца, показана на рис. 1.

Оптическая схема, представленная на рис. 2, позволяет наблюдать доменную структуру визуально. При прохождении линейно-поляризованного света через соседние домены вектор ` Е поворачивается в противоположных направлениях на равные углы j (рис. 3, а). Если анализатор расположить так, чтобы проекция векторов ` Е, прошедших через соседние домены, на плоскость пропускания анализатора была одинаковой, то согласно закону Малюса и интенсивность света после прохождения через домены будет одинаковой, т. е. домены не будут видны (будут видны только переходные области между соседними доменами (доменные границы)). Таких положений два: параллельное расположение плоскости пропускания анализатора и поляризатора и скрещенное. На рис. 3, б эти положения обозначены цифрами 1 и 2 соответственно.

 Если анализатор, находящийся в положении 1 и 2, повернуть на малый угол, то появится изображение доменов, контраст между которыми возрастает с увеличением угла поворота анализатора. Различие в контрасте между доменами максимально тогда, когда угол между одним из векторов ` Е и плоскостью пропускания анализатора p/2. При вращении анализатора
в противоположном направлении темные домены становятся светлыми,
а светлые темными. Измерив угол поворота плоскости пропускания анализатора от положения 1 или 2 до максимального контраста между доменами, можно определить угол поворота плоскости поляризации j.

Так как угол j для исследуемых материалов меньше 45°, то
в положении анализатора 1 интенсивность света больше, чем в положении 2. Измерения более точны, если в исходном состоянии поле зрения темное, т. е. анализатор находится в положении 2. В этом случае плоскость пропускания анализатора надо повернуть на угол j, чтобы добиться наиболее темного изображения одного из доменов (рис. 3, в).

Рис. 1

Рис. 2

в

б

а

Рис. 3

 

Измерение угла поворота плоскости поляризации j для данного образца (по известной толщине l и намагниченности насыщения J_s) позволяет определить постоянную Верде (V) с помощью формулы (1).

     По закону Малюса

 

где I _А  и I _П – соответственно интенсивности света, прошедшие через анализатор и поляризатор. В данном случае для одного домена угол  и он будет темным, для другого 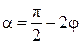 и он будет светлым (рис. 3, в). Согласно закону Малюса контраст между доменами не изменится при изменении угла   на 180^°. Это свойство доменной структуры можно использовать для проверки закона Малюса.

 

Устройство установки

 

Основой установки является микроскоп (рис. 4). Микроскоп состоит из тубуса 1, закрепленного на штативе со станиной 2.
В нижней части тубуса расположен объектив 3,
а в верхней – окуляр 4. В тубус вставлен также анализатор. Тубус помещен над предметным столиком 5, на котором находится кассета
с поляризатором и образцом феррит-граната. Столик может вращаться, и для отсчета его угла поворота, а следовательно, и поляризатора имеется шкала с указателем. Под столиком находится осветительная система 6, в качестве которой может использоваться зеркало или лампа накаливания. Лампа осветителя рассчитана на 220 В. Для наводки на резкость штатив можно перемещать винтом наводки-юстировки 7.

Порядок выполнения работы

1. Перемещая винт грубой наводки на резкость и микровинт, настроить микроскоп так, чтобы отчетливо была видна доменная структура.

2. Контраст между доменами зависит от взаимного расположения анализатора и поляризатора, поэтому при вращении как поляризатора, так и анализатора будет изменяться яркость доменов. В данной установке удобнее вращать поляризатор путем вращения предметного столика микроскопа.

3. Вращая столик микроскопа, найти положение, при котором домены не видны (а видны только доменные границы) и поле зрения будет темно-серым. Записать угол j₀, соответствующий этому положению (рис. 3, б).

4. Вращать столик микроскопа до тех пор, пока контраст между доменами не станет наибольшим, при этом темные домены наблюдаются как темно-коричневые, а светлые — как желтые. Записать угол j₁ (рис. 3, в).

5. Вычислить угол поворота плоскости поляризации j:

 

j =½j₁-j½.

 

6. Описанные выше эксперименты выполнить 5 раз и вычислить среднее значение <j>, данные занести в табл. 1, в которой приведены значения толщины образца l и намагниченности J _s.

 

                                                                                          Таблица 1

 

№	j	j1	j	<j>	Js	l	V
1

4160

Ам