Методика обработки результатов измерения

ИЗУЧЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ

КОСМИЧЕСКИХ ЧАСТИЦ

 

Цель работы: ознакомиться с устройством, принципом работы счетчика Гейгера и методикой измерения радиоактивного излучения: изучение характера распределения космических частиц: освоение методики обработки случайных чисел, используя распределение Пуассона и критерий Пирсона.

 

Объект исследования

 

Космические лучи – это поток частиц, приходящих на Землю из межзвездного пространства. Первичные космические лучи состоят главным образом (на 90 %) из протонов, a-частиц и более тяжелых ядер. Основная доля первичного излучения имеет энергию  до 10¹⁰эВ, но встречаются также частицы со значительно большей энергией (до 10²⁰ эВ). В результате взаимодействия первичных космических лучей с ядрами газов атмосферы появляются новые (вторичные) частицы – мезоны различных сортов, распад которых приводит к появлению электронов, позитронов и фотонов большой энергии. Таким образом, вторичные космические лучи, наблюдаемые на высоте до 10 км, совершенно не похожи по своему составу на первичные космические лучи. Космические лучи, приходящие в низшие слои атмосферы, принято делить на мягкую и жесткую компоненты.

    Мягкая компонента состоит из электронов, протонов и ¡ -квантов, которые сильно поглощаются в веществе. Поглощение частиц мягкой компоненты существенным образом зависит от порядкового номера z вещества. Частицы мягкой компоненты целиком поглощаются десятисантиметровым слоем свинца.

    Жесткая компонента состоит из μ -мезонов, которые слабо поглощаются веществом, причем приблизительно одинаково веществами с разными z. Столь большое различие проникающей способности частиц обоих компонент объясняется тем, что электроны и позитроны мягкой компоненты при взаимодействии с веществом тратят большую часть своей энергии на излучение, а потери μ- мезонов на излучение сравнительно малы.

 

Используемое оборудование

 

    Для исследования мягкой компоненты космического излучения можно использовать счетчики Гейгера-Мюллера, которые широко применяются при обнаружении различного рода радиоактивных и других ионизирующих излучений a -, b - частиц, ¡ -квантов.

Принцип расчета счетчика. Устройство

 

    Счетчик представляет собой газоразрядный промежуток с сильно неоднородным электрическим полем. Чаще всего применяются счетчики с коаксиально расположенными электродами: внешний цилиндр – катод, тонкая нить, натянутая вдоль его оси, – анод. Электроды располагаются в герметически замкнутом резервуаре, наполненном каким-либо газом (гелием, аргоном) под давлением порядка сотен мм рт. ст.

С

Рис. 1

R

    Схема включения счетчика приведена на рис.1. Напряжение между собирающим электродом и анодом счетчика подается от высоковольтного источника. Конденсатор С разделяет цепь питания и входную цепь. Сопротивление R ограничивает ток через счетчик в момент разряда. Импульсы напряжения пересчитываются частотомером в автоматическом режиме.

    Количественно правильная регистрация может производиться счетчиком после исследования его счетной характеристики, которая дает зависимость скорости счета от приложенного напряжения при постоянной интенсивности ионизирующего излучения.

 

Методика обработки результатов измерения

 

    В физике часто приходится встречаться с измерениями, результаты которых представляются в виде целых чисел. Например, через счетчик Гейгера за время измерения проходит не очень большое и при этом    целое число частиц. Статистические закономерности, которые имеют место в этом случае, несколько отличаются от правил обработки полученных результатов и вычисления погрешностей при непрерывном изменении переменной величины.

    Рассмотрим счетчик, регистрирующий космические частицы. В то время как число отсчетов счетчика за любой промежуток времени является целым числом, интенсивность космического излучения целым числом не выражается. Если счетчик исправен, то в числе частиц, зарегистрированных  счетчиком, например за 10 с, погрешности не будет. Тем не менее, если будем повторять эксперимент, то обязательно получим различные значения числа частиц М. Причиной различия являются характерные свойства процесса образования космических частиц, а не погрешности в работе счетчика. Появление каждой частицы в некотором временном интервале связано с определенной вероятностью. Знание этой вероятности позволило бы рассчитать ожидаемое среднее число частиц, проходящих через счетчик за 10 секунд.

    Если эксперимент повторяется много раз, то распределение числа частиц М, наблюдаемых в этом интервале, не отличается от функции, называемой распределением Пуассона, т. е.

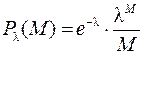                                           ,                                      (1)

где Р _l(М) – вероятность появления числа М; l – параметр распределения.

    Можно показать, что параметр распределения l – это среднее количество частиц, ожидаемое в случае многократного повторения счетного эксперимента, т. е. .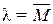

    Интересным свойством распределения Пуассона является то, что параметр распределения l связан со средним стандартным отклонением соотношением .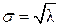

    Для определения ожидаемого числа частиц за рассматриваемый промежуток времени Р _i надо вероятность появления числа М _i умножить на число временных интервалов (опытов) N:

 

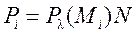                                           .                                       (2)

 

    Распределение Пуассона определено только для положительных значений. На практике оно часто применяется тогда, когда нужно оценить надежность измерений и погрешности в случае наблюдения редких событий.

    В качестве конкретного примера распределения Пуассона рассмотрим эксперимент с космическими частицами. Предположим, что число частиц, попадающих в счетчик за данное время, должно быть распределено
в соответствии с законом Пуассона.

    Выберем N временных интервалов. Измерим с помощью счетчика Гейгера число М -частиц в каждом интервале. Подсчитаем количество интервалов N_i с одинаковым числом M_i и построим таблицу (M_i, N_i, P_i), расположив M_i в порядке возрастания. Эта таблица может быть использована для построения графика (гистограммы) в координатах (M_i, N_i), являющегося экспериментальным распределением космических частиц. Определим среднее значение числа частиц за один временной интервал по формуле

,                                               (3)

где  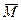является наилучшей оценкой для параметра распределения Пуассона.

    Учитывая, что 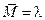, абсолютную погрешность можно определить по формуле

 

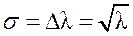 или ,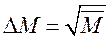

а относительную

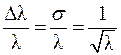 или .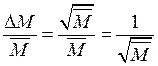

 

Используя 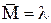, по формуле (1) рассчитаем вероятность P_i (M _i) для всех M_i, по формуле (2) найдем ожидаемое число частиц P_i, занесем его в таблицу (M_i, N_i, P_i). Эти значения P_i можно использовать для построения графика распределения Пуассона в координатах (M_i, P_i), в виде гладкой кривой. Гистограмма же имеет ступенчатый вид.

    Исследование проблемы достоверности гипотез производится с помощью критериев значимости. Наиболее удобным из критериев значимости является так называемый критерий “хи-квадрат”, в котором в качестве меры принимается сумма квадратов отклонений от предлагаемой зависимости, поделенная на число степеней свободы:

 

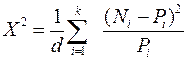                                – критерий Пирсона, (4)

 

где d – число степеней свободы, которое определяется из формулы

 

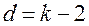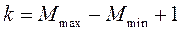                             ; .                        (5)

 

Здесь вычитается число 2 потому, что в распределении Пуассона используются две связи для определения параметра распределения и стандартного отклонения 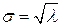, которые исключаются из общего числа наблюдений K. Отклонение экспериментальных точек от значений принятой гипотезы измеряется в долях стандартной погрешности измерения. Найденное значение “хи-квадрат” должно быть сопоставлено с теорией. Для этого следует воспользоваться таблицей приложения, где для различного числа степеней свободы приведены значения вероятностей в процентах. При сравнении отклонений с данными обычно применяют следующую терминологию: если найденная из эксперимента величина “хи-квадрат” такая, что вероятность составляет, например 95 %, то отклонение данных от ожидаемых совершенно не существенно: если 5 %, то ожидаемую гипотезу нельзя исключить, но она ставится под сомнение: если – 0,1 %, то можно утверждать, что проверяемая гипотеза, возможно, является ошибочной (отклонения являются “высоко значимыми”). Вероятность от 1 до 5 % называют “почти значимыми”. При вероятности больше 5 % следует считать, что экспериментальные данные недостаточны для того, чтобы отвергнуть гипотезу. В этом заключается краткое изложение метода обработки результатов наблюдений. Подробнее об этом можно прочесть в [2, 4].

 

Порядок выполнения работы

 

 

Контрольные вопросы

 

1. Как устроен и работает счетчик Гейгера? Начертите схему включения счетчика и объясните принцип ее работы.

2. Что вы знаете о характере распределения космических частиц в верхних слоях атмосферы?

3. Как показать, используя таблицу ”хи-квадрат”, подтверждают ли проведенные измерения предполагаемое распределение космических частиц?

4. Напишите формулы для вычисления:

распределения Пуассона;

дисперсии для распределения Пуассона;

критерия Пирсона ”хи-квадрат”.

 

Литература

 

1. Савельев, И. В. Курс общей физики / И. В. Савельев. – М.: Наука, 1978, 1979. – Т. 2, 3.

2. Практикум по ядерной физике / ред. В. О. Сергеев. – М.: Высш. шк., 1975.

3. Руководство к лабораторным занятиям по физике / ред.
Л. Л. Гольдин. – М.: Наука, 1973.

4. Сквайрс, Дж. Практическая физика / Дж. Сквайрс. – М: Мир, 1971.

5. Тейлор, Дж. Введение в теорию ошибок / Дж. Тейлор. – М.: Мир, 1995.

Поделиться:

Воспользуйтесь поиском по сайту: