 |
Начальное значение для суммы равно нулю, для произведения - единице.
|
|
|
|
Следует обратить внимание на то, что количество блоков проверки условий в блок-схемах разветвляющихся алгоритмов всегда на единицу меньше, чем число различных ветвей.
Так, в примерах 1 и 2 для получения двух ветвей используется один блок проверки условия, в примере 3 для получения трех ветвей используются два блока проверки условия.
Пример 4. Составить блок-схему вычисления значения величины y при k, принимающем целые значения в диапазоне от 1 до 3.


При разработке блок-схемы задачи следует сделать проверку значения k на принадлежность данному диапазону. Если k не принадлежит диапазону от 1 до 3, пользователю необходимо выдать сообщение об этом и предложить повторить ввод k.

При составлении программы проверку k на диапазон выполнять перед вводом исходных данных.
Пример 5.Составить блок-схему вычисления значения величины y, в зависимости от значения x.


 |
13. Задачи с циклической алгоритмической структурой.
Рассмотрим примеры типовых циклических алгоритмов.
Блок-схемы алгоритмов с заданным числом повторений цикла.
Пример 1.Составить блок-схему вычисления суммы и произведения натуральных чисел. Цикл простой, с заданным числом повторений, без переадресации.
s=1+2+3+4+5+......+n
Определение суммы и произведения нескольких величин требует начального присваивания переменным, обозначающим сумму и произведения (в данном примере S и P).Без такого присваивания результаты могут не соответствовать действительности из-за возможного использования этих величин каким-то другим образом до цикла или при повторном выполнении цикла.
Начальное значение для суммы равно нулю, для произведения - единице.
|
|
|

Пример 2. Цикл с монотонным изменением параметра.
Составить блок-схему вычисления значений функции y= -364*x2/(x5-1) при изменении x от a до b с шагом h.
При решении такого типа задач мы получаем таблицу значений функции y. Поэтому, такие задачи называются задачами табулирования функции. Циклы с монотонным изменением параметра можно организовать двумя способами:
1) проверка выхода из цикла осуществляется по достижении конца интервала изменения аргумента.
Цикл сложный, т.к. внутри цикла есть разветвление, без переадресации, т.к. значения параметра x, шаг изменения параметра h и значения функции y находятся в фиксированных полях памяти.
Телом цикла являются блоки 4 - 9.
Тело цикла выполняется до тех пор, пока значение переменной цикла x не превысит конечное значение b. (Рис.1)
2) выход из цикла осуществляется по заданному числу повторений, т.е. по количеству точек, на которые разбивается интервал, в зависимости от величины шага h. (Рис.2)
Число точек, на которые разбивается интервал, определяется по формуле
N=[(b-a)/h]+1,
где a, b - начальное и конечное значения интервала, h-шаг изменения параметра x, [] обозначают антье(entier)-целую часть числа, не превосходящую данного.
Например, если a=-10,b=10,h=0.1,то N=[(10+10)/0.1]+1 = 201
 |
 |
14. Циклы с переадресацией
Цикл, содержащий операторы, изменяющие адреса операндов при каждом его повторении, называется циклом с переадресацией. С помощью таких циклов на ЭВМ реализуется обработка массивов.
Массив - это упорядоченная совокупность элементов, обладающих одинаковыми свойствами.
Операнды - это данные любой природы, над которыми производятся действия в программе.
15. Примеры алгоритмы обработки массивов
Главной особенностью алгоритмов обработки одномерных массивов является то, что обработка массивов должна производиться поэлементно. Это означает, что надо организовать такой циклический алгоритм, который обеспечит возможность обращения к необходимым элементам массива (или массивов) и их последующую обработку. Именно поэтому в качестве переменной цикла обычно используется индекс элементов.
|
|
|
В рассматриваемых ниже алгоритмах обработки массивов процессы ввода и вывода элементов массива изображаются одним блоком, который подробно можно изобразить следующим образом:

Схема вывода элементов массива аналогична схеме ввода и отличается от нее только тем, что отсутствует блок ввода n.
В момент выхода из цикла переменная цикла имеет значение, превышающее максимально допустимое (i=n+1).
Пример 1.Составить блок-схему вычисления суммы S и произведения P элементов одномерного массива a1, a2, a3,…, an.
 |
Пример 2. Найти сумму и количество компонент вектора a (a1, a2, a3,…, an), принадлежащих отрезку [c, d], а все компоненты, меньшие с, заменить на единицу.
 |
Пример 3.Дан вектор X(x1, x2, x3,…, xn).Если у вектора есть хотя бы одна компонента < D, то все отрицательные компоненты заменить их квадратами, оставив остальные без изменения. В противном случае, т.е., если у вектора нет компонент больших числа D, домножить вектор на число С.
 |
Пример 4.Дан вектор X(x1, x2, x3,…, xn).Найти максимальный элемент и его номер.
 |
16. Итерационные циклы
Итерационные циклы применяются для решения математических задач методом итерации, т.е. последовательного сближения. К итерационным циклам сводятся вычисления ex, sinx, cosx и других степенных рядов. Итерационный процесс можно в общем виде описать следующей формулой:
yi+1=f(xi+1, yi,k),
где yi+1-результат вычислений при (i+1)-вом исполнении цикла;
xi+1-значения аргументов при (i+1)-вом исполнении цикла;
yi-результат вычислений при i-том исполнении цикла;
k- необходимые константы.
Итерационный процесс может быть реализован на машине только в том случае, если он является сходящимся. Простой итерационный цикл содержит четыре блока:
1) задание начальных значений аргумента и функции;
2) вычисление текущего значения аргумента;
3) вычисление текущего значения функции;
4) логический блок, проверяющий условие выхода из цикла.
|
|
|
Итерационные циклы имеют следующие особенности:
исходные данные и результаты (аргументы и функции) хранятся в фиксированных ячейках памяти, т.е. итерационный цикл не содержит команд с изменяемыми адресами;
результаты вычислений предыдущего выполнения цикла используются в качестве исходных данных для последующего выполнения цикла;
начальные значения переменных выбираются произвольно, но в соответствии с характером тех формул, которые предстоит реализовать в программе;
Число повторений цикла может быть известно программисту заранее или может быть выбрано из соображений точности вычислений, но может быть и неизвестно.
При известном числе итераций можно использовать цикл for (пошаговый, с выходом из цикла по достижению параметром цикла конечного значения).
При неизвестном числе итераций момент выхода из цикла определяется самой программой по достижению заданной точности вычислений. Проверка точности вычислений осуществляется путем выполнения логической операции отношения:
|yi+1-yi|<= eps, где
yi+1 и yi -два соседних приближения, а 0<=eps<1,любая наперед заданная величина - точность вычислений (eps должно быть положительным и достаточно малым, например,0.1, 0.01, 0.001 и т.п.).
Следует обратить внимание на то, что сравниваться должны абсолютные величины, а результат сравнения редко приводит к нулю, т.к. трудно получить полное соответствие между точностью результата и заданной точностью его вычисления. Кроме того, бывает трудно оценить, сколько итераций выполнит машина, поскольку количество повторений цикла зависит от величины eps и скорости сходимости итерационного процесса.
Пример 1. Рассмотрим пример итерационного цикла, позволяющего вычислить y = ex с помощью степенного ряда:
y=ex=1+x+x2/2!+x3/3!+x4/4!+.....+x n/n!+......= x n/n!
где n=0,1,2,3,......
Данная формула может быть представлена в виде циклического итерационного процесса, который описывается рекуррентными соотношениями между членами ряда yi и частными суммами si.
Выведем рекуррентную формулу, которая позволяет сократить вычисления.
|
|
|
Обозначим через u n - n- ый член ряда. Тогда
u n+1=xn+1/(n+1)!, а un=x n/n!
Найдем отношение un+1 к u n:

Следовательно, в общем виде рекуррентная формула имеет вид:
 , где n=0,1,2,3,......
, где n=0,1,2,3,......
 |
Пример 2. Составить блок-схему вычисления y= x по итерационной формуле Ньютона: yn+1=(x/ yn+yn), где yn, yn+1 - n-ое и (n+1)-ое приближения соответственно, а n=0,1,2,3,... нулевое приближение задается равным b, где b - число, близкое к вычисляемому и которое задает сам программист.
Процесс вычислений прекратить, как только два соседних приближения будут отличаться на величину eps>0, которая определяет точность вычислений и которую задает сам программист, т.е. должно выполняться условие
|yn+1-yn|<=eps
Например, вычислим y= 5 с точностью eps=0.0001=10-4
Возьмем n=0, нулевое приближение y0 =2.
I итерация:
y1=1/2*(x/y0+y0)=1/2*(5/2+2)=2.25
|y1-y0|=|2.25-2|=0.25 <= 0.0001 -нет,
II итерация: n=1
y2=1/2*(x/y1+y1) =1/2*(5/2.25+2.25)=2.2361
|y2-y1|=|2.2361-2.25|=|-0.0139|=0.0139<=0.0001 -нет,
III итерация: n=2
y3=1/2*(x/y2+y2) =1/2*(5/2.2361+2.2361)=2.2361
|y3-y2|=|2.2361-2.2361|=|0|<=0.0001 -да.
Следовательно, y= 5=2.2361 с заданной точностью eps=0.0001.
Если увеличить точность eps(0.000001,0.0000001 и т.д.), то количество итераций может увеличиться и соответственно увеличится число значащих цифр после запятой (точки).
 |
Аналогично составляются блок-схемы вычисления функций
y=sinx=x-x3/3! + x5/5!-x7/7!+......+(-1) n+1*x2n+1/(2n+1)!+......
Вычисления прекратить, как только очередной член ряда по модулю станет меньше eps,т.е.|un+1|<=eps.
Рекуррентная формула выводится следующим образом:
u n=(-1) n+1*x2n+1/(2n+1)! un+1=(-1) n+2*x2n+3/(2n+3)!
Формула для un+1 члена ряда получается, если вместо n в формулу для un подставить n+1 и произвести соответствующие арифметические действия.
Найдем отношение un+1 к un:

Следовательно, в общем виде рекуррентная формула имеет вид:
 , где n=0,1,2,3,......
, где n=0,1,2,3,......
Вывод рекуррентной формулы для
y=cosx=1-x2/2!+x4/4!-x6/6!+......+(-1) n+1*x2n/(2n)!+......
производится аналогично.
 , где n=0,1,2,3,......
, где n=0,1,2,3,......
17. Вложенные циклы
Одним из видов сложных циклов являются вложенные циклы, которые содержат несколько включенных друг в друга циклов. Среди циклов различают внешние и внутренние циклы.
Цикл, который не входит в другие циклы, называется внешним.
Цикл, который включается в другие циклы, называется внутренним.
Каждый из этих циклов имеет элементы, характерные для простых циклов: счетчики циклов, блоки изменения параметров, рабочую часть и др.
Особенность выполнения сложного цикла состоит в том, что за одно исполнение внешнего цикла внутренний цикл повторяется многократно.
Правильное повторное исполнение внутреннего цикла возможно только в том случае, если изменяемые в процессе вычислений параметры этого цикла будут восстановлены в их первоначальном виде, т.е. будут восстановлены счетчики, индексы, рабочие поля и другие изменяемые элементы.
|
|
|
Это достигается тем, что во внешний цикл вводится специальный блок, который восстанавливает изменяемые параметры внутреннего цикла. Перед каждым обращением к внутреннему циклу должен выполняться блок восстановления параметров.
Типичным примером тройного цикла является умножение матриц: даны две вещественные квадратные матрицы а(n*n) и b(n*n).Получить матрицу с(n*n),равную произведению двух матриц a и b по формуле: сij= ai k*bk j; (i,j=1,n)
 | |||
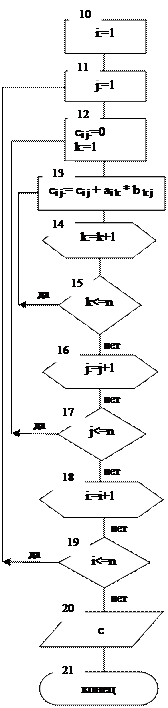 | |||
Элементы матриц вводятся и располагаются в памяти машины последовательно по строкам.
Ввод элементов матрицы осуществляется двойным циклом
(блоки 2-9).
Блок 2 - ввод размерности матриц,
блок 3 - задает начальное значение переменной i - номера строки,
блок 4 - задает начальное значение переменной j - номера столбца,
блок 5 - ввод значений элементов матриц a, b (поочередно, по одному),
блок 6 - увеличение номера столбца,
блок 7 - проверка условия выхода из внутреннего цикла,
блок 8 - увеличение номера строки,
блок 9 - проверка условия выхода из внешнего цикла - конец цикла ввода по условию "нет".
Внешний цикл по i (блоки 10-19) обеспечивает вычисление всех элементов матрицы c.
Внутренний цикл по j (блоки 11-17) обеспечивает вычисление элементов одной строки матрицы c.
Внутренний цикл по k (блоки 12-15) обеспечивает вычисление одного элемента матрицы c. Элемент на пересечении строки с номером i и столбца с номером j матрицы c получается путем суммирования произведений n элементов i-той строки матрицы a на соответствующие n элементов j-того столбца матрицы b. Это достигается перебором всех элементов i-той строки и j-того столбца с помощью индекса k.
Внешний цикл по i повторяется n раз, внутренний цикл по j повторяется n2 раз, внутренний цикл по k повторяется n3 раз.
Блок 20 - вывод результирующей матрицы c на печать. Осуществляется двойным циклом, аналогично развернутой блок-схеме ввода элементов матриц a и b (блоки 3-9).
18. Заключение
Современный специалист, независимо от профессиональной области должен владеть информационными технологиями, то есть участвовать в процессе производства, обработки, хранения и передачи информации с использованием современных технических средств. Это связано, прежде всего, с высокими требованиями, которые предъявляются на рынке труда.
Целью учебно-методического пособия «Алгоритмы и технология их разработки» является изучение и освоение стратегии проектирования алгоритмов, эвристических методов конструирования алгоритмов, базовых принципов построения рациональных алгоритмов, критериев хорошего алгоритма, понятие алгоритмизации, свойства алгоритмов, общие принципы построения алгоритмов, использовать Госты ЕСПД при оформлении блок-схем алгоритмов.
В методическом пособии изложен теоретический и практический материал. В теоретической части даны достаточно подробные сведения, необходимые для получения основных сведений об изучаемой теории алгоритмов, в практической части приведены упражнения, закрепляющие изученный теоретический материал.
Методика, которая положена в основу пособия, позволяет существенно ускорить процесс закрепления знаний, освоить новый материал, необходимый для осуществления профессиональной деятельности при освоении сложных дисциплин по выбранной специальности в сфере профессиональной деятельности.
Пособие может быть рекомендовано в помощь преподавателям дисциплин «Информатика», «Информационные технологии»,«Основы алгоритмизации и программирования», а также для самостоятельной работы студентов.
Литература
1. Закон РФ: «О стандартизации» от 10.06. 1993;
2. Единая система программной документации (ЕСПД). М., Изд-во стандартов, 2000
3. В.А. Гвоздева «Введение в специальность программиста» М., ИД «Форум» - Инфра – М 2007
4. Ю.А. Шафрин «Информационные технологии». М., Лаборатория базовых знаний, 2000
5. С.В. Симонович Информатика. СПб.: Питер, 2002
6. Информатика: Учебник под ред. проф. Н.В. Макаровой. М., Финансы и статистика, 2000
|
|
|


