Введение в анализ. Комплексные числа. Основные теоретические сведения.

ВЫСШАЯ МАТЕМАТИКА

 

Методические указания к выполнению контрольных заданий

для студентов-заочников

специальностей 240100.62 «Химическая технология»,

230400.62 «Информационные системы и технологии»

полной и сокращенной формы обучения

 

 

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

 

 

Балаково 2011

 

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ.

 

Перед выполнением контрольного задания студент должен изучить соответствующие разделы курса по учебным пособиям в разделе «Литература» настоящих методических указаний. В начале каждой контрольной работы номера необходимых для этой работы пособий указываются в квадратных скобках. В методических указаниях даются также некоторые начальные теоретические сведения и приводятся решения типовых примеров.

Задачи контрольной работы выбираются из таблицы вариантов, помещенной в конце методического пособия, согласно тому варианту, номер которого совпадает с последней цифрой учебного номера (шифра) студента. Контрольную работу следует выполнять в тетради (отдельной для каждой работы) чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. В заголовке работы должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы. Заголовок работы надо поместить на обложке тетради; здесь же следует указать дату отсылки работы в институт и адрес студента. Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными соответствующего номера. Решения задач излагать подробно и записывать аккуратно, объясняя все действия и делая необходимые чертежи. После получения прорецензированной работы (как не зачтенной, так и зачтенной) студент должен исправить в ней все отмеченные ошибки и недочеты.

При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента.

 

 

4Вариант

 

 

Контрольная работа № 1.

Аналитическая геометрия. Элементы векторной и

линейной алгебры.

 

Л и т е р а т у р а: [1], гл.III, IX, X; [2], §1-6, § 7-13; [4], гл. VII, § 1-5; [5], гл. I, II, III; [6], гл. I, II, III.

 

1.Совокупность чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей.

Обозначают матрицу буквами А,В,С,…

 

Матрица размером m x n.

 

а₁₁,а_12,…,а_mn-элементы матрицы.

Коротко записывают так: А=(а_ij), где i-номер строки, j-номер столбца. Матрица размера n x n называется квадратной матрицей n-го порядка.

Элементы a₁₁,a₂₂,…,а_nn образуют главную диагональ матрицы, элементы а_m1,а_m-1,2…,а_1,n-побочную диагональ матрицы. Матрица А=(а11,а12,…,а1n) называется матрицей-строкой размером 1 х n.

Матрица - матрица-столбец размером m x 1.

Квадратная матрица - называется единичной матрицей.

Матрица А^т, которая получается из данной матрицы А заменой строк столбцами, называется транспонированной к А:

 

 

Произведением матрицы А=(а_ij), имеющей m строк и k столбцов, на матрцуВ=(в_ij), имеющую k строк и n столбцов, называется матрица С=АВ=(с_ij), имеющая m строк и n столбцов, каждый элемент с_ij которой равен сумме произведений элементов i-й строки матрицы А и j-го столбца матрицы В:

 

С_ij=а_i1в_1j+а_i2в_2j+…+а_ikа_kj

 

2.Определитель- это число, поставленное по определенным правилам в соответствие квадратной матрице.

Обозначается D=detА=

Определитель второго порядка:

 

 

Определитель третьего порядка:

 

(1)

 

Вычисляется по правилу треугольника. Схематически это выглядит так:

 

 

Минором М_ij какого-либо элемента определителя n-го порядка называется определитель n-1 порядка, получаемый из данного определителя вычеркиванием i строки и j столбца, на пересечении которых стоит элемент.

Например: , - миноры элементов a₁₁ и a₃₁ определителя D.

Алгебраическим дополнением А_ij какого-либо элемента а_ij называется его минор М_ij, умноженный на (-1)^i+j,где i,j –номера строки и столбца элемента а_ij:

 

A_ij=(-1)^i+jM_{ij (2)}

 

Матрица А^-1 называется обратной по отношению к матрице А, если выполняется равенство:

A^-1A=AA^-1=E

 

Если определитель D матрицы А не равен 0, то обратная матрица вычисляется по формуле:

, (3)

где - присоединенная матрица, составляется из алгебраических дополнений следующим образом:

(4)

 

1. Элементарными называются следующие преобразования матриц:

а) перестановка строк (столбцов),

б) умножение строк (столбцов) на число, отличное от 0,

в) прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на число.

При помощи элементарных преобразований любую прямоугольную матрицу можно привести к ступенчатому виду. Схематично ступенчатая матрица изображена на рисунке:

 

 

Не заштрихованная часть матрицы занята нулями. В клетках, покрытых двойной штриховкой, стоят ненулевые элементы. Они называются угловыми элементами. Остальные элементы могут быть произвольными.

Число r угловых элементов ступенчатой матрицы В не зависит от способа приведения матрицы А к ступенчатому виду и называется рангом матрицы А. Обозначается r(А)=r(В)=r

3. Система 3-х линейных уравнений с тремя неизвестными х₁,х₂,х₃ имеет вид:

 

(5)

 

где а_ij – коэффициенты системы, b_i- свободные члены.

Определитель 3-го порядка D, составленный из коэффициентов при неизвестных, называется определителем системы:

 

 

Решение системы методом Крамера: Если определитель системы D не равен нулю, то решение находится по формулам Крамера:

, (6)

 

где определители D₁, D₂, D₃ вычисляются следующим образом:

 

Систему (5) можно записать в матричной форме:

АХ=В, (7)

где

 

Решение системы (1) матричным способом: Если определитель системы D не равен 0, то решение системы имеет вид:

 

Х=А^-1В (8)

 

4.Вектором называется отрезок с определенным на нем направлением.

Обозначается .

Координатами вектора в прямоугольной системе координат в пространстве называются его проекции на оси координат О_х, О_у, О_z.

Обозначается

Х= пр_Ох =х₂-х₁

У= пр_Оу =у₂-у₁ (9)

Z= пр_Оz =z₂-z_1,

 

где точка А(х₁,у_1,z₁)-начало вектора, В(х₂,у_2,z₂)- конец вектора.

Длина вектора вычисляется по формуле:

(10)

Вектор может быть разложен по базису , т.е. представлен в виде:

 

5.Скалярным произведением двух векторов 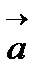и называется число, определяемое равенством:

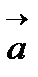
= , (11)

где - угол между векторами и .

Выражение скалярного произведения двух векторов через координаты векторов:

= _, (12)

где ,

7. Векторным произведением двух векторов и называется вектор

1) длина его вычисляется по формуле

= ,

-угол между векторами и ,

2) вектор перпендикулярен векторам и ,

3) векторы _, , образуют правую тройку.

 

Выражение векторного произведения через координаты векторов и :

= , (13)

где Х₁,У₁,Z₁- координаты вектора , Х₂,У₂,Z₂- координаты вектора .

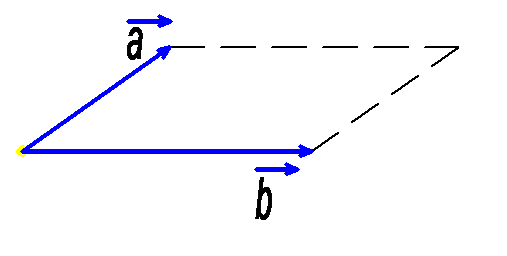Геометрически длина векторного произведения равна площади параллелограмма, построенного на векторах и : S_пар-ма=

 

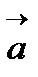8. Смешанным произведением трех векторов _, , называется число, равное скалярному произведению вектора и векторного произведения х :

= ( х )

 

Выражение смешанного произведения векторов через их координаты:

= ,

где Х₁,У₁,Z₁- координаты вектора , Х₂,У₂,Z₂- координаты вектора , Х₃,У₃,Z₃- координаты вектора .

Модуль смешанного произведения векторов _, , равен объему параллелепипеда, построенного на этих векторах:

 

 

9.Общее уравнение плоскости S имеет вид:

 

Ах+Ву+Сz+D=0 (14)

 

Где - нормальный вектор плоскости.

 

Уравнение плоскости, проходящей через три точки М₀(х₀,у₀,z₀), М₁(х₁,у₁,z₁), М₂(х₂,у₂,z₂) имеет вид:

(15)

Угол между двумя плоскостями S₁ и S₂ определяется как угол между их нормальными векторами и , определяется из формулы:

(16)

 

10.Уранения прямой в пространстве, проходящей через две точки М₀(х₀,у₀,z₀), М₁(х₁,у₁,z₁) имеют вид:

 

(17)

 

Пример 1. По координатам вершин пирамиды А₁(2,-3,1), А₂(-1,-4,2), А₃(4,-1,2), А₄(3,-4,2) найти: 1.длины ребер А₁А₂ и А₁А₃; 2. угол между ребрами А₁А₂ и А₁А₃; 3. площадь грани А₁А₂А₃; 4. объем пирамиды А₁А₂А₃А₄.

Р е ш е н и е.

1.Находим векторы

Длины этих векторов, т.е. длины ребер А₁А₂ и А₁А₃ таковы:

2. Скалярное произведение векторов находим по формуле (12):

 

Косинус угла между векторами находим по формуле:

 

3. Площадь грани А₁А₂А₃ равна половине площади параллелограмма, построенного на векторах , т.е. половине длины векторного произведения этих векторов:

 

 

4) Объем V пирамиды равен объема параллелепипеда, построенного на векторах .

Координаты вектора

 

Пример 2. Найти угол между плоскостью Р₁, проходящей через точки А₁(2,-3,1),А₂(-1,-4,2),А₃(4,-1,2) и плоскостью Р₂, проходящей через точки А₁,А₂,А₄(3,-4,2).

Р е ш е н и е. Находим уравнения плоскостей Р₁ и Р₂ по формуле (16):

(x-2)(-3)-(y+3)(-5)+(z-1)(-4)=0

3x-5y+4z-25=0-уравнение плоскости Р₁, - нормальный вектор плоскости Р₁.

(x-2)0-(y+3)(-4)+(z-1)4=0 y+z+2=0- уравнение плоскости Р_2, - нормальный вектор плоскости Р₂.

Угол между плоскостями находим по формуле (17)

Пример 3. Составить уравнение прямой, проходящей через точки А₁(2,-3,1) и А₂(-1,-4,2).

Р е ш е н и е. Используя формулу (12), получаем:

-уравнение искомой прямой.

 

Пример 4. С помощью формул Крамера найти решение системы:

Р е ш е н и е. Находим определитель системы:

Так как D 0, то решение системы находим по формулам Крамера:

Находим D₁,D₂,D₃:

;

;

.

Получаем решение системы: \=

 

Пример 5. Дана система линейных уравнений

Найдем решение системы уравнений методом Гаусса. Разделим первое уравнение на 2. Затем умножим обе части этого уравнения на (-3) и прибавим их к соответствующим частям третьего уравнения, и, умножив на (-5), прибавим к соответствующим частям третьего уравнения. В результате получим систему:

Разделим обе части второго уравнения на 7/2, после этого умножим обе части полученного второго уравнения на (-15/2) и сложим их с соответствующими частями третьего уравнения, в результате получим систему:

Из последнего уравнения находим z=3, затем из второго найдем у=-2, из третьего найдем х=1.

 

 

ВВЕДЕНИЕ В АНАЛИЗ. КОМПЛЕКСНЫЕ ЧИСЛА. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Л и т е р а т у р а: [1], гл. 4; [3], гл. 3; [4], гл. II; [5], гл. VI; [6], гл. IV.

 

1.Полярная система координат представляет собой полюс О и полярную ось ОЕ с выбранным на ней масштабом.

Произвольная точка М в полярной системе координат имеет две координаты (), где - полярный радиус, - полярный угол.

 

Рассмотрим полярную и прямоугольную системы координат такие, что полюс совпадает с началом координат, а полярная ось – с положительной полуосью Ох.

Прямоугольные координаты (х,у) точки М и ее полярные координа-

ты () связаны соотношениями:

 

,

, (1) 2. Определение конечного предела в точке:

Число А называется пределом функции при , если для любого существует такое, что для всех значений х из области определения функции, удовлетворяющих неравенству , выполняется неравенство:

Обозначим или при

Функция называется бесконечно малой при , если .

Функция называется бесконечно большой при , если .

Две функции и одновременно стремящиеся к нулю или к бесконечности при , называются эквивалентными, если

Обозначим

Предел отношения бесконечно малых (бесконечно больших) функций не изменяется, если каждую из них заменить эквивалентной функцией, т.е.

 

, если , . (19)

3. К основным элементарным функциям относятся:

1) Степенная функция ,

2) Показательная функция ,

3) Логарифмическая функция ,

4) Тригонометрическая функция , , , ;

5) Обратные тригонометрические функции: , , , .

Предел элементарной функции в точке, принадлежащей области определения функции равен ее значению в этой точке, т.е. .

При вычислении пределов могут получаться неопределенности вида: , , , , . Элементарными приемами раскрытия неопределенностей являются:

1) Сокращение на множитель, создающий неопределенность;

2) Деление числителя и знаменателя на старшую степень аргумента (при );

3) Применение эквивалентных бесконечно малых и бесконечно больших;

4) Использование двух замечательных пределов;

 

- I замечательный предел

 

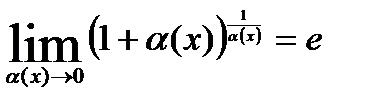- II замечательный предел

 

Отметим также, что: , если ;

 

, если , ,число

 

, если , ;

 

, если , .

 

 

4. Функция называется непрерывной в точке , если:

1) функция определена в точке ;

2) существуют конечные односторонние пределы функции:

 

, ;

 

3) односторонние пределы равны:

;

4) предельное значение функции в точке равно ее значению : .

Обозначим .

Точка называется точкой устранимого разрыва, если (нарушается условие 4).

Точка называется точкой разрыва первого рода, если оба односторонних предела конечны, но (нарушается условие 3).

Точка называется точкой разрыва второго рода, если не существует хотя бы один из односторонних пределов (нарушение условия 2).

 

5. Выражение вида называется комплексным числом (в алгебраической и тригонометрической форме соответственно) , - мнимая единица,

- действительная часть, - мнимая часть комплексного числа , - модуль и аргумент числа .

Если известны действительная x и мнимая часть , то находим по формулам: , .

Если известны и , то x, y находим по формулам: , .

Комплексные числа изображаются точками на комплексной плоскости (рис.)

Извлечение корня n-й степени (n-натуральное число) из числа производится по формуле:

 

;

где - арифметический корень из модуля 2, = 0, 1,2,…, n-1.

6. Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра).

Если r – радиус окружности, а точка С (a, в) – ее центр, то уравнение окружности имеет вид .

 

Если центр окружности совпадает с началом координат, то ее уравнение

 

 

7. Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Если фокусы эллипса находятся на оси Ох на равных расстояниях от начала координат в точках F₁(с,0) и F₂(-c,0), то получится простейшее (каноническое) уравнение эллипса:

,

где 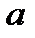- большая полуось,

- малая полуось.

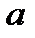, и с (половина расстояния между

фокусами) связаны соотношением

 

8. Гиперболой называется множество точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Если поместить фокусы гиперболы в точки F₁(-c, 0) и F₂(c, 0), то получится каноническое уравнение гиперболы: , где 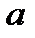- действительная полуось, - мнимая полуось, 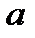, , с связаны соотношением .

 

9. Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Если директрисой параболы является прямая , а фокусом – точка

F , то уравнение параболы имеет вид: .

 

В зависимости от расположения фокуса и директрисы парабола имеет следующий геометрический вид и уравнение:

 

 

10. Под параллельным переносом осей координат понимают переход от системы координат Охy к новой системе О₁х₁y₁, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными.

Если (х₀, y₀) – координаты начала координат О₁ новой системы в старой системе координат,

(х, y) – координаты произвольной точки М в старой системе Охy, - координаты точки М в новой системе Ох₁y₁, то следующие формулы позволяют находить старые координаты х и y по известным новым и наоборот: .

 

Пример 1. Изобразить на комплексной плоскости числа:

1) , 2) .

Записать число 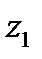в тригонометрической, а число - в алгебраической форме.

Р е ш е н и е. 1) Для числа 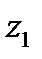имеем , . Откладывая по оси Ох , а по оси Оy , получаем точку комплексной плоскости, соответствующую числу .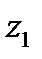

Запишем число 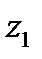в тригонометрической форме: Модуль числа находим по формуле

.

Аргумент определяем по формуле: .

Так как число четверти, то .

Тригонометрическая форма имеем вид: .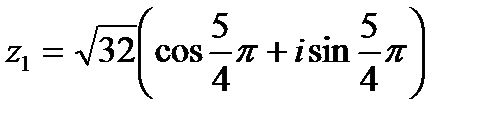

2) Модуль числа равен , а аргумент . Для изображения этого числа на комплексной плоскости проводим из полюса луч под углом к полярной оси и откладываем на нем отрезок длиной . Полученная точка соответствует числу .

Его действительная часть , а мнимая часть . Таким образом, алгебраическая форма числа имеем вид .

Пример 2. Вычислить (см. пример 9).

Р е ш е н и е. Используя формулу, получаем

 

=0, 1, 2

 

При =0 ;

 

При =1 ;

 

При =2

 

Пример 3. Привести уравнение кривой второго порядка к каноническому виду с помощью параллельного переноса осей координат. Определить вид кривой и построить ее график.

Р е ш е н и е. Выделим в левой части полный квадрат по переменной х:

Делим левую и правую часть на 9:

- это уравнение эллипса.

Чтобы записать уравнение в каноническом виде, нужно осуществить параллельный перенос, т.е. перейти к новым координатам: .

Получим каноническое уравнение эллипса:

= 3 – большая полуось,

= - малая полуось.

 

Поделиться:

Воспользуйтесь поиском по сайту: