 |
Тема: Сетевая транспортная задача
|
|
|
|
Тема: Марковские процессы
Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени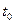 
вероятностные характеристики процесса не зависят от того, как система пришла в это состояние. То есть, в марковских процессах будущее зависит от прошлого только через настоящее.
Процесс называется процессом с дискретными состояниями, если его возможные состояния можно перенумеровать или перечислить, и система приходит из одного состояния в другое практически мгновенно.
Процесс называется процессом с дискретным временем, если переходы из одного состояния в другое возможны только лишь в определенные моменты времени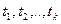 
.
Марковские процесс с дискретным состоянием и дискретным временем называется марковской цепью.
Если в момент времени 
система находилась в состоянии 
то вероятность того, что в момент времени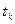 
система перейдет в состояние 
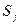обозначают 
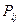и называют переходной вероятностью.
Если рассматривать переход за m – этапов, то в качестве промежуточного этапа можно рассматривать любой момент времени. Имеет место уравнение Колмогорова-Чекмана:
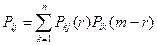
Вероятность того, что после k-того шага и до k+1 шага система будет находится в состоянии называется состоянием цепи Маркова. И она обозначается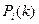 
:
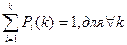
Распределение вероятностей состояний в начале процесса обозначается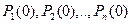 
и называется начальным распределением вероятностей.
Марковым была доказана теорема: если матрица переходов Т такая, что она не содержит нулевых элементов, то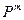 
стремится к некоторой ненулевой матрице 
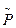при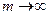 
Тема: Элементы теории игр в стратегическом виде:
Правилом принятия решения первого игрока называется многозначное отображение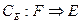 
следующим образом: каждой стратегии y соответствует 
|
|
|
Пара стратегий (x,y), где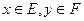 
называется бистратегией.
Бистратегия (x,y) называется несогласованной парой стратегий, если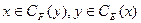 
.
Пара стратегий (x*,y*) называется оптимальной бистратегией по Парето, если не существует других бистратегий (x,y), которые принесли бы каждому из игроков прибыли большие, чем бистратегии (x*,y*).
Тема: Сетевая транспортная задача
1. Графом будем называть произвольную систему отрезков, определенным способом соединенных между собой. Эти отрезки, если им присвоено направление будем называть дугами графа, иначе – ребрами графа.
Точки, которые являются началами или концами дуг или ребер графа будем называть вершинами графа. Каждая из вершин будет обозначаться номером, а дуги графа будем обозначать, как упорядоченные пары i-j, где i – начало дуги, j – ее конец. Такие вершины i(i,j), которые обозначаются дугами будем называть инцидентными.
2. Путь в графе – это последовательность дуг (i1,i2), (i2,i3),.., (
), конец каждой из которых совпадает с началом следующей, кроме последней.
3. Контуром в графе называется путь, у которого начало и конец совпадают.
4. Граф ϝ называется сильно связанным, если каждые две вершины i(i,j) можно соединить некоторым путем, который ведет из i в j.
Замечание! Если в определениях (2-4) понятие дуги заменить на понятие ребра, то получим определения понятий цепи, цикла, связанного графа соответственно.
5. Деревом называется граф, который не имеет циклов и в котором каждая пара вершин соединена некоторой цепью.
6. Транспортной сетью ϻ будем называть произвольный граф Ϝ составным частями которого (дугам, вершинам и ребрам) поставлены в соответствие некоторые параметры, которые определяют их свойства.
При том вершины такого графа отожествляются со станциями, пунктами отправки и приема товара, базами и складами. А дуги или ребра представляют собой пути сообщения между смежными пунктами. Таким образом, транспортная сеть ϻ будем отождествлять со следующим набором объектов:
|
|
|
ϻ = <Ϝ, A, C, D, Rb, Pp,Dt>, где:
Ϝ – граф, представляющий пути сообщения между пунктами;
A – множество вершин графа, при чем A=Ab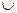 
At 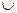Ap, где Ab – множество станций отправителей товара, At – множество транзитных станций, Ap – пункты назначения.
С={Cij} – массив значений стоимостей перевозок;
D={dij} – массив числовых значений пропускаемых возможностей путей между смежными станциями или пунктами.
Rb={Ri, для всех i є Ab} – объемы продукции на станциях-отправителях, которые подлежат перевозке.
Pp={Pi, для всех i є Ap} – объемы потребностей в продукции станций назначения.
Dt={ Di, для всех i є At} – пропускная способность транзитных станций или иначе максимальные объемы продукции, которые могут принять на сохранения склады.
|
|
|
