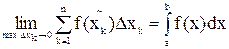|
Интегрирование методом подстановки
|
|
|
|
Определенный интеграл
Задачи, приводящие к понятию определенного интеграла
Задача о площади криволинейной трапеции.
Опред. Криволинейной трапециец называют фигуру, ограниченную графиком непрерывной функции y=f(x) (f(x)=0), осью 0х и прямыми х=а, х=b

Вычислим площадь такой фигуры
Заметим, что:
1) площадь есть неотрицательное число;
2) равные фигуры имеют равные площади;
3) площадь всей фигуры равна сумме площадей частей, на которые разбита эта фигура.
Для решения этой задачи разобьем отрезок [a, b] произвольным способом на n малых отрезков точками
х0 = а, х1, х2, …, хn = b
Обозначим длины этих отрезков через 

 …,
…, 
Обозначим через mк и Мк через наименьшее и наибольшее значения функции f(x) на к-ом элементарном отрезке [хк-1, хк].
Построим на каждом элементарном отрезке, как на основании, два элементарных прямоугольника: «входящий» с высотой mк и «выходящий» с высотой Мк. Их площади будут соответственно равными  и
и  .
.
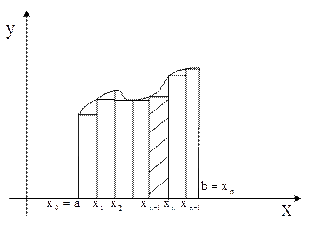
 - сумма площадей всех «входящих» прямоугольников, т. е. площадь вписанной ступенчатой фигуры (рис. 1)
- сумма площадей всех «входящих» прямоугольников, т. е. площадь вписанной ступенчатой фигуры (рис. 1)
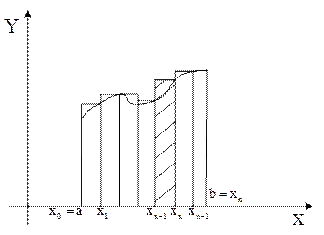
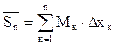 - сумма площадей всех «выходящих» прямоугольников, т. е. площадь описанной ступенчатой фигуры (рис. 2)
- сумма площадей всех «выходящих» прямоугольников, т. е. площадь описанной ступенчатой фигуры (рис. 2)
S – площадь криволинейной трапеции
При любом разбиении отрезка [a, b] имеем следующее двойное неравенство:
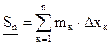

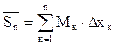 (1)
(1)
Для любого числа n Sn и Sn – будут определены, т. е. известны. А S – мы должны будем определить.
Построим теперь на элементарных отрезках [хк-1, хк] прямоугольники третьего вида: высота каждого прямоугольника равна 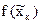 ,
,
где хк-1  хк,
хк,
а значит mк  Мк
Мк
Площадь такого прямоугольника равна 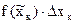 .
.
Площадь фигуры, составленной из таких прямоугольников

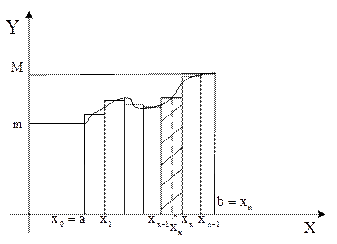
Сама эта фигура (рис. 3), есть ступенчатая фигура, занимающая некоторое промежуточное положение между фигурами, состоящими из всех «входящих» прямоугольников (рис. 1) и всех «выходящих» прямоугольников (рис. 2)
|
|
|
 (2)
(2)
или кратко 
Это неравенство справедливо при всяком n и любом способе разбиения отрезка [a, b] и при любом выборе точки  в элементарных отрезках. Из рисунка 3 видим, что
в элементарных отрезках. Из рисунка 3 видим, что
 >
> 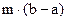 и
и  <
< 
C увеличением числа n, 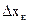 -- уменьшается, величина
-- уменьшается, величина  - монотонно возрастает, оставаясь
- монотонно возрастает, оставаясь  <
<  ,
,
величина  - монотонно убывает, оставаясь
- монотонно убывает, оставаясь  >
> 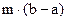
Это значит, что существуют пределы  и
и  при
при 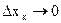 (свойство пределов)
(свойство пределов)

Из равенства (2) следует, что 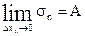 (свойство пределов)
(свойство пределов)
Но А = S – площадь криволинейной трапеции.
Следовательно 
Площадь криволинейной трапеции называется предел, к которому стремится площадь ступенчатой фигуры (рис. 3), составленной из элементарных прямоугольников, когда 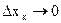 .
.
Задача о работе переменной силы.
Пусть под действием некоторой силы F материальная точка М движется по прямой OS, причём, направление силы совпадает с направлением движения. Требуется найти работу, произведённую силой F при перемещении точки М из положения s = a в положение s = b.
1) если сила F=const, то A=F(b-a). Работа равна произведению силы на длину пути.
2) Предположим, что сила F непрерывно меняется в зависимости от положения материальной точки, т.е. представляет собой функцию F(s), непрерывную на отрезке [a,b]. Разобьём отрезок [a,b] на n произвольных частей с длинами  . На каждом частичном отрезке
. На каждом частичном отрезке  выберем произвольную точку
выберем произвольную точку 
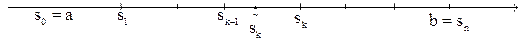

Предполагая, что сила на каждом элементарном отрезке сохраняет постоянное значение равное, 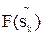 , найдём работу на пути
, найдём работу на пути 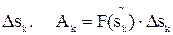 ,
,
а  будет приближённое значение выражение работы силы F на всём отрезке [a,b]. Предел этой суммы при
будет приближённое значение выражение работы силы F на всём отрезке [a,b]. Предел этой суммы при 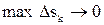 и выражает работу силы F(s) на пути от точки S = a до точки S = b.
и выражает работу силы F(s) на пути от точки S = a до точки S = b.
 .
.
Определённый интеграл.
Пусть на отрезке [a,b] задана непрерывная функция 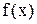 . Разобьем отрезок [a,b] произвольным образом на n частей точками
. Разобьем отрезок [a,b] произвольным образом на n частей точками  где
где  . Обозначим
. Обозначим  внутри отрезка выберем произвольно точку
внутри отрезка выберем произвольно точку  и вычислим значения функции
и вычислим значения функции  Сумма произведений вида
Сумма произведений вида
|
|
|


Называется интегральной суммой для функции f(x) на отрезке [a,b]. Т. к. функция f(x) – непрерывна, то  где
где  соответственно наименьшее и наибольшее значения функции f(x) на отрезке [xk-1, xk]. Умножая все члены последнего неравенства на
соответственно наименьшее и наибольшее значения функции f(x) на отрезке [xk-1, xk]. Умножая все члены последнего неравенства на  получим
получим

Если  на отрезке [a,b], геометрический смысл последнего неравенства мы разбирали.
на отрезке [a,b], геометрический смысл последнего неравенства мы разбирали.
Предел 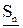 и
и 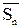 существует и не зависит от способа разбиения отрезка [a,b] на части, причём
существует и не зависит от способа разбиения отрезка [a,b] на части, причём  .
.
На основании свойства пределов существует  .
.
Определение: если при любых разбиениях отрезка [a,b], и при любом выборе точек  на отрезках [xk-1, xk] интегральная сумма
на отрезках [xk-1, xk] интегральная сумма 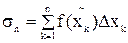 стремится к одному и тому же пределу S, то этот предел называют определённым интегралом от функции f(x) на отрезке [a,b] и обозначают
стремится к одному и тому же пределу S, то этот предел называют определённым интегралом от функции f(x) на отрезке [a,b] и обозначают  .
.
|
Число a называют нижним пределом,
b- верхним пределом. Отрезок [a,b] называют отрезком интегрирования, Х-переменной интегрирования.
Если  на отрезке [a,b], то
на отрезке [a,b], то  численно равен площади криволинейной трапеции, ограниченной кривой y=f(x), прямыми x=a, x=b и осью ОХ
численно равен площади криволинейной трапеции, ограниченной кривой y=f(x), прямыми x=a, x=b и осью ОХ

Замечание1: Определённый интеграл зависит только от вида ф-ии f(x) и пределов интегрирования, но не зависит от переменной интегрирования, которую можно обозначить любой буквой.
 .
.
Замечание2: из определения определённого интеграла следует, что  .
.
Замечание3: при a=b, 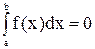 .
.
Пар.12. Основные свойства определённого интеграла.
1) постоянный множитель можно выносить за знак определённого интеграла  , где А-const.
, где А-const.
2) определённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме от интегралов слагаемых.

3) если на отрезке [a,b], где а<b, функции f(x) и 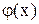 удовлетворяют условию f(x)
удовлетворяют условию f(x) 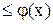 , то
, то  .
.
4) если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и 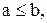 то
то 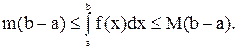
5) теорема о среднем.
Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдётся такая точка  что справедливо следующее равенство
что справедливо следующее равенство 
6) для любых трёх чисел a, b, c справедливо равенство, 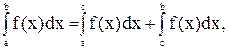 если только эти три интеграла существуют.
если только эти три интеграла существуют.
Доказать все эти свойства самостоятельно.
§13 Вычисление определённого интеграла.
Формула Ньютона-Лейбница.
Пусть в определённом интеграле  нижний предел а закреплён, а верхний предел b меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть ф-ия верхнего предела.
нижний предел а закреплён, а верхний предел b меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть ф-ия верхнего предела.
|
|
|
Перейдём к привычным обозначениям: верхний предел обозначим через x, а переменную интегрирования через t.
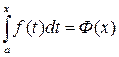 , где a – const.
, где a – const.
Если f(t)≥0, то Ф(х) – численно равна площади криволинейной трапеции аАХх (Рисунок 1).
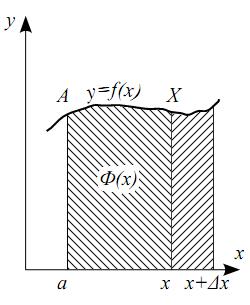
Рисунок 1 – График функции f(x).
Теорема 1. Если ф-ия f(x) – непрерывная функция и 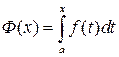 , то имеет место равенство Ф‘(х) = f(x).
, то имеет место равенство Ф‘(х) = f(x).
Или: производная от определённого интеграла по верхнему пределу равна подынтегральной ф-ии, в которую вместо переменной интегрирования подставлено значение верхнего предела.
Док-во. По определению производной имеем:
 ;
;

По теореме о среднем:
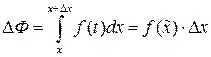 , где
, где 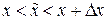
Найдём  .
.
След-но 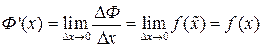 ,
,
т.к. 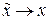 при
при  . Теорема доказана.
. Теорема доказана.
Замечание. Из доказанной теоремы следует, что если ф-ия f(t) – непрерывна на отрезке [a, x], то сущ-ет ф-ия 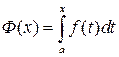 и она является первообразной для ф-ии f(x), то справедлива формула:
и она является первообразной для ф-ии f(x), то справедлива формула:
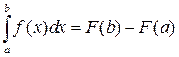 (1)
(1)
Эта формула наз. формулой Ньютона-Лейбница.
Док-во. Пусть F(x) – есть некоторая первообразная от ф-ии f(x). По теореме 1 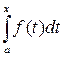 есть такая же первообразная от ф-ии f(x), а две первообразные от данной ф-ии отличаются на постоянное слагаемое С*:
есть такая же первообразная от ф-ии f(x), а две первообразные от данной ф-ии отличаются на постоянное слагаемое С*:
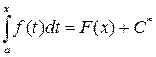 . (2)
. (2)
Это равенство при соответствующем значении С* верно для всех х, т.е. являются тожд-ом.
При х = а имеем:
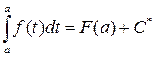 ;
;
0 = F(a)+C*, откуда С* = - F(a).
При х = b равенство (2) будет:
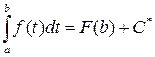 .
.
Заменив переменную t на х получим ф-лу Ньютона-Лейбница:
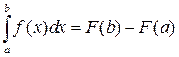 .
.
Её можно, при решении, записать так:
 .
.
Примеры:
1. 
2. 
3. 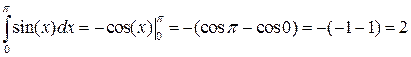
§14 Методы вычисления определённого интеграла
14.1 Интегрирование по частям.
Пусть u и v – дифференциальные ф-ии, тогда:
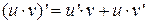
Интегрируя обе части в пределах от а до b получим:
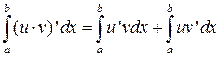 ;
;
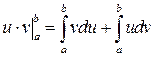 ;
;
откуда: 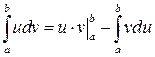 .
.
Пример: 
Интегрирование методом подстановки
Теорема: Пусть дан интеграл:
 ,
,
где ф-ия f(x) непрерывна на отр. [a,b].
Введём новую переменную:
 .
.
Если 1) 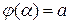 ,
,  ;
;
2) 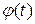 и
и  непрерывны на отр.
непрерывны на отр.  ;
;
3)  определена и непрерывна на отр.
определена и непрерывна на отр.  ,
,
то 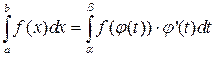 (1)
(1)
Док-во: Если F(x) первообразная для ф-ии f(x), то можем написать следующее равенства:
 (2)
(2)
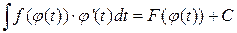 (3)
(3)
Из равенства 2 получаем
|
|
|
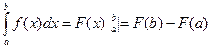
Из равенства 3 получаем
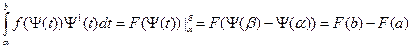
Правые части этих выражений равны, следовательно, равные и левые.
Пример.  14.3)Интегрирование нечетных и четных функций на отрезке, симметричном относительно нуля.
14.3)Интегрирование нечетных и четных функций на отрезке, симметричном относительно нуля.
Пусть  - непрерывная функция на отрезке
- непрерывная функция на отрезке  симметричном относительно нуля.
симметричном относительно нуля.
А)  -нечетная функция, т.е.
-нечетная функция, т.е. 
Докажем, что 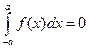
 4
4

Подставим в равенство 4

Итак, определенный интеграл с противоположными пределами от нечетной непрерывной функции равен нулю.
Пример.  , т.к. функция
, т.к. функция  есть нечетная функция.
есть нечетная функция.
б)  -нечетная функция, т.е.
-нечетная функция, т.е. 
Докажем, что 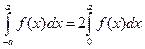 5
5
Используем равенство 4 и
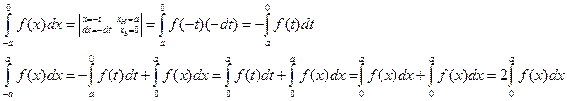
Итак, определенный интеграл с противоположными пределами от четной непрерывной функции равен удвоенному интегралу от этой функции, взятому по правой половине отрезка интегрирования.
&15.Несобственные интегралы.
15.1)Интегралы с бесконечными пределами.
Пусть функция  определена и непрерывна при всех x, удовлетворяющих неравенству
определена и непрерывна при всех x, удовлетворяющих неравенству
 .Рассмотрим интеграл
.Рассмотрим интеграл 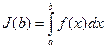 , b>a
, b>a


у
 |
0 a b х
 При изменении в интеграл изменяется.Пусть b
При изменении в интеграл изменяется.Пусть b 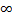
Определение.Если существует конечный предел  ,то этот предел называют несобственным интегралом от функции
,то этот предел называют несобственным интегралом от функции  на интервале
на интервале 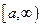 и обозначают
и обозначают
 . Следовательно
. Следовательно 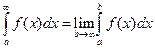
Если  существует, то говорят несобственный интеграл
существует, то говорят несобственный интеграл  сходится.
сходится.
Если этот предел не существует или равен ∞, то говорят несобственный интеграл расходится.
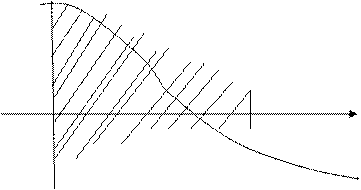
В случае  выражает площадь неограниченной области, заключенной между линиями
выражает площадь неограниченной области, заключенной между линиями 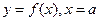 и осью OX. Аналогично определяются несобственные интегралы вида
и осью OX. Аналогично определяются несобственные интегралы вида

Для последнего равенства, если сходятся оба интеграла, стоящих справа, то сходится и интеграл, стоящий слева.Если хотя бы один из них расходится, то расходится и интеграл, стоящий слева.
Примеры.

Несобственный интеграл сходится.
2) 
Не существует (нет определенного значения).Следовательно несобственный интеграл расходится.
Во многих случаях достаточно установить сходится данный интеграл или расходится и оценить его значение. В этих случаях можно воспользоваться следующими теоремами, которые запишем без доказательства.
Теорема 1. Если для всех х (х≥а) выполняется неравенство 0≤f(X)≤Y(x)
и если 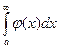 сходится, то
сходится, то  также сходится и при этом
также сходится и при этом 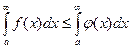
Пример.
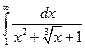

Вспомогательная функция 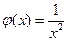
 при всех
при всех 
 сходится
сходится
Следовательно и данный несобственный интеграл сходится.
Теорема 2. Если для всех 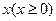 выполняется неравенство
выполняется неравенство  , причем
, причем 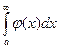 расходится, то расходится и
расходится, то расходится и  .
.
Пример. 
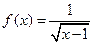 ,
, 
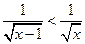 при всех
при всех 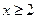
 расходится следовательно данный несобственный интеграл расходится.
расходится следовательно данный несобственный интеграл расходится.
Теорема 3.Если  сходится, то сходится и интеграл
сходится, то сходится и интеграл  .
.
В этом случае последний интеграл называется абсолютно сходящимся.
|
|
|
Пример. 

 сходится.
сходится.
Следовательно данный несобственный интеграл сходится.
15.2) Интеграл от разрывной функции
Пусть функция  определена и непрерывна при
определена и непрерывна при 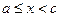 , а при
, а при  функция либо не определена, либо терпит разрыв.
функция либо не определена, либо терпит разрыв.
В этом случае нельзя говорить об интеграле  как о пределе интегральных сумм.В этом случае его определяют так:
как о пределе интегральных сумм.В этом случае его определяют так:
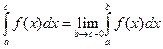
Если это предел существует, то говорят несобственный интеграл  сходится, в остальных случаях расходится.
сходится, в остальных случаях расходится.
Если функция  определена и непрерывна при
определена и непрерывна при 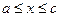 , то
, то

Если функция  терпит разрыв при
терпит разрыв при 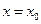 , где
, где  , то
, то

В последнем равенстве, если оба интеграла, стоящие в правой части, сходятся, то сходится и интеграл, стоящий в левой части.
Если хотя бы один из интегралов, соящих в правой части равенства расходится, то расходится и интеграл, стоящий в левой части.
Пример.

При 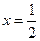 функция
функция  разрывна,
разрывна,
 , т.е. интеграл сходится.
, т.е. интеграл сходится.
Для определения сходимости несобственных интегралов от разрывных фукций и оценки их значений часто применяют теоремы, аналогичные теоремам для интегралов с бесконечными пределами.
Теоремы сформулировать самостоятельно.
Примеры.
1)  при х=1 функция
при х=1 функция  разрывна
разрывна

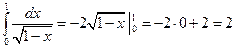 сходится
сходится
Следовательно, данный интеграл от разрывной функции сходится.
2)  функция
функция 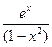 при
при 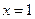 разрывна
разрывна
 при
при 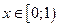
 расходится
расходится
Следовательно  расходится.
расходится.
&16. Вычисление площади фигуры
16.1) Площадь фигуры в декартовой системе координат.
Мы уже рассматривали как вычисляется, площадь криволинейной трапеции, в случае когда  на отрезке
на отрезке 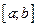
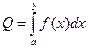 (рис.1)
(рис.1)
Если  на отрезке
на отрезке 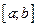 , то
, то 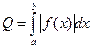 (рис.2)
(рис.2)

у




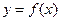

0 a b х
Рис.1









 у
у
0 х
а b
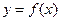 рис.2
рис.2




 у
у
 | |||
 | |||
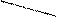
 0 a b х
0 a b х
Рис.3
Если функция F(x) конечное число раз меняет знак на отрезке [a,b], то отрезок [a,b] разбивают на части, где F(x) будет знакопостоянной (рис.3) и площади суммируют. Если область ограничена 4), то замкнутым контуром (рис. 
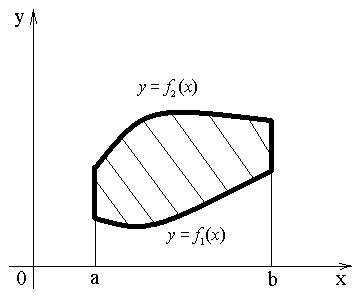
Рис.4
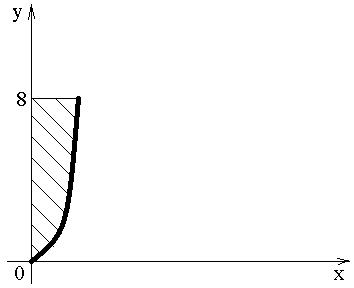
Пример. 1) Найти площадь фигуры, ограниченной кривой  , прямой y=8 и осью OY.
, прямой y=8 и осью OY.

2)Найти площадь фигуры, ограниченной линиями 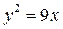 и y=3x
и y=3x
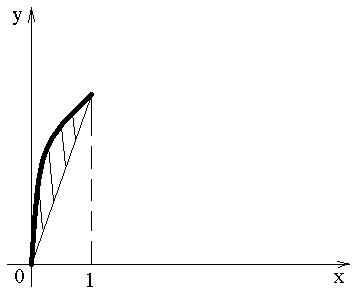
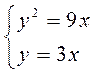



 ,
, 
 16.2) Площадь фигуры в полярной системе координат.
16.2) Площадь фигуры в полярной системе координат.
При вычислении площади в полярной системе координат простейшей фигурой является криволинейный сектор ОАВ с вершиной в полюсе.
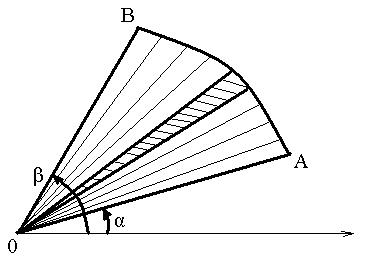
Криволинейный сектор ОАВ ограниченного кривой ρ=F(Ө) и лучами Ө=α, Ө=β. Разобьем данную область лучами 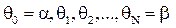 на n частей.
на n частей.
Площадь элементарного сектора заменим круговым сектором, площадь которого:
 ,
,
где  .
.
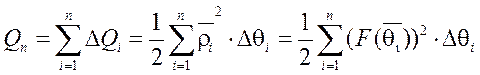
Эта сумма есть интегральная сумма для функции  на отрезке
на отрезке  , поэтому
, поэтому  или
или

|
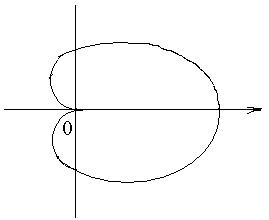
Пример. Вычислить площадь области, ограниченной кардиоидой 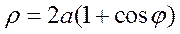 ,
, 
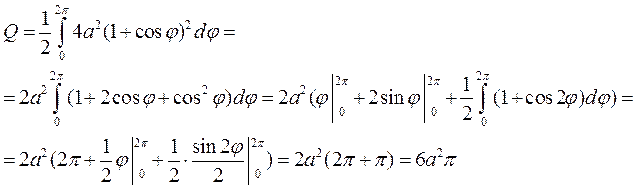
17. Длина дуги кривой.
17.1)Длина дуги кривой в прямоугольных координатах.
В прямоугольных координатах на плоскости дана кривая уравнением y=F(x)

Найдем длину дуги AB. В дугу АВ впишем ломанную  абсциссы т.
абсциссы т.  соответствуют
соответствуют 
 - длина одного звена ломанной.
- длина одного звена ломанной.
Длина ломанной 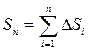
Длиной дуги АВ называют тот предел, к которому стремится длина вписанной ломанной, когда 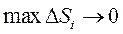
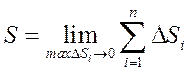

По теореме Лагранжа имеем:
 , где
, где  <
<  <
< 
Следовательно 
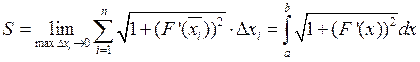

|
Замечание 1 Кривая задана параметрически
x=x(t)
y=y(t), 
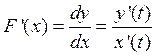 dx=x’(t)dt
dx=x’(t)dt
 или
или

|
Замечание 2 Задана пространственная кривая параметрически
x=x(t)
y=y(t) 
z=z(t)
 
|
Примеры.
1) Найти длину дуги AB цепной линии
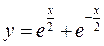 от т.(0;2) до т.(2;
от т.(0;2) до т.(2;  )
)
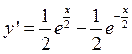
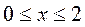
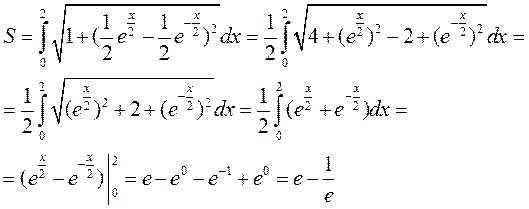
2) Вычислить длину L первого витка винтовой линии
x=acost 
y=asint 

z=bt 

Длина дуги кривой в полярных координатах.
Уравнение кривой в полярной системе координат: 
 формулы связывающие прямоугольные и полярные координаты имеют вид:
формулы связывающие прямоугольные и полярные координаты имеют вид:
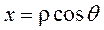
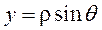
Подставляя вместо  выражение из уравнения кривой получим параметрические уравнения кривой
выражение из уравнения кривой получим параметрические уравнения кривой

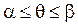
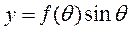
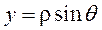


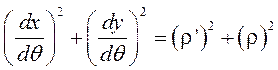 (проверить самостоятельно)
(проверить самостоятельно)

Пример. Вычислить длину кардиоиды 
Т.к. кривая симметрична относительно полярной оси, то 
Для S1 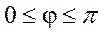
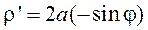
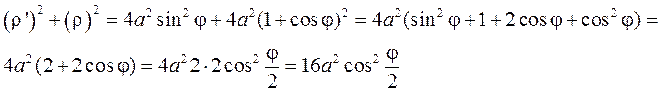

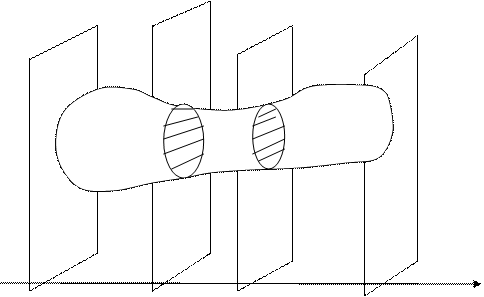
18.1) Вычисление объема тела по площадям параллельных сечений.
Имеем некоторое тело Т. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси ОХ. Эта площадь будет зависеть от положения секущей плоскости, т.е. являться функцией от х.
S=S(x).
Разобьем это тело на слои плоскостями x0=а,х1,,…,xn=b
В каждом частичном отрезке  выберем т.
выберем т.  и вычислим
и вычислим 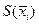 .Построим цилиндрическое тело с основанием
.Построим цилиндрическое тело с основанием  и высотой
и высотой  .
.
Объем этого цилиндра 
Заменяя каждый слой таким цилиндром и просуммировав, получим

Х
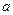

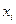

Предел этой суммы называют объемом тела T (при max  )
)
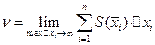
Т.к.  - представляет интегральную сумму, получим
- представляет интегральную сумму, получим

Пример.Вычислить объем цилиндрического отрезка, т.е. тела, отсеченного от прямого кругового цилиндра плоскостью, проходящей через диаметр основания.
Пусть радиус основания цилиндра равен a, высота цилиндрического отрезка H
Ось ОХ – диаметр PQ S(X) – площадь прямоугольного треугольника (на чертеже заштрихована) Этот треугольник подобен 



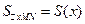 ;
;  ;
;  A
A

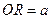 ;
; 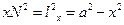
 ;
;  ;
;


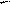




 P M H
P M H



 Объем тела
Объем тела  Q х
Q х
18.2) Объём тела вращения

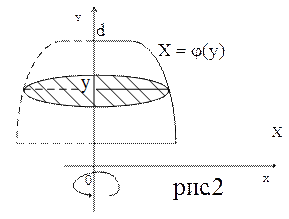
Рис1. криволинейная трапеция вращается вокруг оси ОХ.
S(x) представляет окружность с радиусом y=f(x).
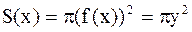
|
Рис2. криволинейная трапеция вращается вокруг оси OY.
S(Y) представляет окружность с радиусом x=  .
.
|