 |
Структуры на основе списков. Работа со стеком и очередью.
|
|
|
|
Пусть S – стек, а – элемент стека. Основные операции при работе со стеком:
Empty(S): Boolean проверка стека на пустоту
a:=Pop(S) получить верхний элемент стека
Push(S,a) добавить элемент в стек
Для работы с очередью используются те же операции. Особенности их применения обсуждались выше
19)
Древовидная структура является одним из способов представления иерархическойструктуры в графическом виде. Древовидной структурой называется благодаря тому, что граф выглядит как перевернутое дерево. По этой же причине говорят, что корневой узел (корень) находится на самом верху, а листья — внизу.
В теории графовдерево — связанный ациклический граф (иногда его называют направленным ациклическим графом, у которого каждая вершина имеет степень 0 или 1). Ациклический граф без жесткого условия связывания иногда называется лесом (так как он состоит из деревьев).
Из совокупности древовидных структур состоят неоднородные семантические сети.
Терминология и свойства
Каждая конечная древовидная структура содержит элемент, не имеющий вышестоящего. Этот элемент называется «корнем» или«корневым узлом». Он может считаться первым (или стартовым) узлом. Обратное утверждение, в общем случае, неверно: бесконечные древовидные структуры могут иметь, а могут и не иметь корневые узлы.
Линии, связывающие элементы называются «ветвями», а сами элементы называются узлами. Узлы без потомков называются «конечными узлами» или «листьями».
Названия связей между узлами именуются по принципу семейных взаимосвязей. На Западе в области информатики, в основном используются только названия членов семьи мужского рода, в русском языке для обозначения узла, напрямую связанного с узлом-родителем и находящимся в иерархии ниже, часто называют «дочерним». В лингвистике (англоязычной, к примеру), напротив, используются названия членов семей женского рода. Это свидетельствует о возврате к соглашению об общепринятых правилах наименования, авторами которого студентки известного американского лингвиста Ноама Хомского. Несмотря на это, в информатике нейтральные названия «родитель» и «дитя» часто заменяются словами «отец» и «сын», кроме того термин «дядя» не менее активно используется для обозначения других узлов, находящихся на том же уровне, что и родитель.
|
|
|
· Узел является «родителем» другого узла, если он расположен на один шаг выше в иерархии дерева, то есть находится ближе к корневому узлу.
· «Дети» («брат» или «сестра») имеют общий родительский узел.
· Узел, связанный со всеми нижележащими узлами называется «предком» или «предшественником».
В приведенном выше примере, «энциклопедия» является родителем по отношению к «науке» и «культуре», которые соответственно, являются ее «детьми». «Искусство» и «ремесло» являются братьями по отношению друг к другу и детьми по отношению к «культуре».
Древовидные структуры используются для отображения все видов информации из области таксономии, как например, генеалогическое древо, филогенетическое дерево, грамматическая структура языка (например, в английском языке, хорошим примером является схема S → NP VP, означающая, что предложение (sentence) является именной группой (noun phrase) и глагольной группой (verb phrase), способ логического упорядочивания веб-страниц на сайте и так далее.
В древовидной структуре может быть один и только один путь от одной точки до другой точки.
Древовидные структуры широко используются в информатике (смотри Дерево (структура данных) и Связь (техника)).
24) Топологическая сортировка — упорядочивание вершин бесконтурного ориентированного графа согласно частичному порядку, заданному ребрами орграфа на множестве его вершин. Пример
|
|
|
Для графа 
Бесконтурный ориентированный граф
существует несколько согласованных последовательностей его вершин, которые могут быть получены при помощи топологической сортировки, например:
· 
· 
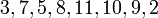
Видно, что в последовательности могут быть переставлены любые две стоящие рядом вершины, которые не входят в отношение частичного порядка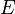 
.
[править]Алгоритм
Пусть дан бесконтурный ориентированный простой граф 
. Через 
обозначим множество вершин таких, что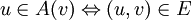 
. То есть, 
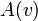— множество всех вершин, из которых есть дуга в вершину 
. Пусть 
— искомая последовательность вершин.
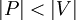выбрать любую вершину такую, что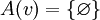 
и 
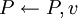удалить из всех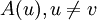 
Наличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину .
[править] Пример работы алгоритма
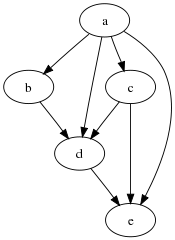
Пусть задан граф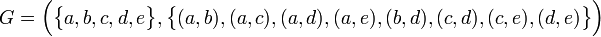 
. В таком случае алгоритм выполнится следующим образом:
| шаг |
| 
| 
| 
| 
| 
|
|
| 
| 
|
| 
| 
|
| |
|
|
|
|
| 
| 
|
| |
|
|
|
| 
| 
| 
| |
|
|
|
|
|
|
| 
| |
|
|
|
|
|
|
| 
| |
|
|
|
|
|
| 
|
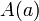
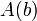
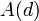
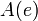
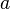
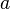
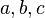
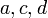
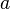
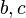
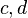
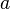
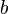
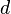
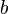
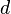
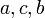
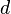
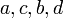
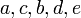
На втором шаге вместо может быть выбрана вершина 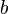, поскольку порядок между 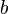и не задан.
|
|
|
