 |
Эмпирический анализ и исследование производительности для каждого алгоритма в отдельности. Оценка количества сравнений, обменов и времени работы алгоритма.
|
|
|
|
Отчет
о выполнении лабораторной работы №1
на тему: «Алгоритмы сортировки. Анализ производительности и визуализация»
по курсу «Алгоритмы и анализ сложности»
| Выполнила: | студентка гр. ПС-08-1 Антонюк П. И. |
| Проверил: | ст. преп. Довгай П. А. |
Днепропетровск
Содержание
1. Постановка задачи.
2. Псевдокод алгоритмов.
3. Эмпирический анализ и исследование производительности для каждого алгоритма в отдельности. Оценка количества сравнений, обменов и времени работы алгоритма.
4.Сравнение производительностей алгоритмов для массивов из 
элементов по количеству размеров и сравнений. Рассмотреть 3 слчая.
5. Графическое представление полученных данных, вывод на основе их о принадлежности алгоритмов к классам.
Постановка задачи.
Рассмотреть 2 группы алгоритмов сортировки – элементарные и более эффективные алгоритмы сортировки. Выполнить их анализ.
Мною рассматриваются следующие элементарные алгоритмы: сортировка выбором(selection sort) и простая сортировка вставкой(straight insertion sort) и более эффективные – алгоритм сортировки слиянием(merge sort) и быстрая сортировка(quick sort).
Псевдокод алгоритмов.
Вход: массив A, состоящий из элементов A[0], A[1],..., A[n-1]
Выход: отсортированный массив.
· сортировка выбором
Описание: Алгоритм находит в массиве минимальный элемент и меняет его местами с первым элементом. Далее алгоритм повторяет эти два действия для еще не отсортированной части массива, пока массив не закончится.
for i =0,1,…,n-2
begin
min = i
for j = i + 1, i+2,…,n-1
if A[j] < A[min] then min = j
if A[min]!=A[i] then Swap(A[i], A[min])
endfor
· простая сортировка вставкой
Описание: Рассматриваются массивы размером 2, 3,…, n элементов и в них поочередно сравниваются два соседних элемента
|
|
|
for i = 1,2,…,n-1
begin
j = i
while j > 0 and A[j - 1] > A[j]
begin
Swap(A[j], A[j-1])
j=j-1
endwhile
endfor
· сортировка слиянием
Описание: Сначала делим список на кусочки (по 1 элементу), затем сравниваем каждый элемент с соседним, сортируем и объединяем. В итоге, все элементы отсортированы и объединены вместе.
function Merge_Sort(A, n)
begin
mid_point = n / 2
return Merge(Merge_Sort(A.Take(mid_point), n), Merge_Sort(A.Skip(mid_point), n), n)
end
function Merge(mass1, mass2, n)
begin
a = 0, b = 0
int[] merged = new int[mass1.Length + mass2.Length]
for i = 0, 1,…, mass1.Length + mass2.Length-1
begin
if b < mass2.Length and a < mass1.Length then
begin
if mass1[a] > mass2[b] and b < mass2.Length then
begin
b:=b+1
merged[i]:= mass2[b]
endthen
else
begin
a:= a+1
merged[i]:= mass1[a]
endelse
endthen
else
if b < mass2.Length then
begin
b:=b+1
merged[i]:= mass2[b]
endthen
else
begin
a:= a+1
merged[i]:= mass1[a]
endelse
endfor
return merged
endfunction
· быстрая сортировка
Описание: Выбираем элемент, называемый опорным, сравниваем все остальные элементы с опорным. На основании сравнения разбиваем множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие -равные -большие. Повторяем рекурсивно для «меньших» и «больших».
function qSort(A, low, high)
begin
i = low
j = high
x = A[(low + (high-low)/2)]
do
begin
while A[i] < x
i=i+1
while x < A[j]
j=j-1
if i <= j then
begin
Swap(A[i], A[j])
i=i+1
j=j-1
endif
enddo
while i <= j
if low < j then qSort(A, low, j)
if i < high then qSort(A, i, high)
return A
endfunction
Эмпирический анализ и исследование производительности для каждого алгоритма в отдельности. Оценка количества сравнений, обменов и времени работы алгоритма.
Входные данные – массив размерности n – оцениваются размером массива и степенью отсортированности: не отсортированный, полностью отсортированный и отсортированный в обратном порядке.
· сортировка выбором
Алгоритм сортировки выбором относится к не рекурсивным алгоритмам.
Основная операция – сравнение.
Количество основных операций зависит от данных.
|
|
|
Количество основных операций:
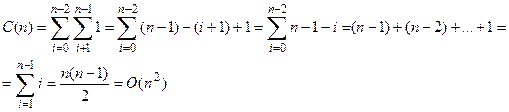
То есть алгоритм сортировки выбором относится к квадратичному классу эффективности, поэтому он не эффективный для сортировки массивов больших чисел.
Количество сравнений для всех случаев одинаковое. Для случая отсортированного массива количество обменов равно нулю.
· простая сортировка вставкой
Алгоритм простой сортировки вставками относится к не рекурсивным алгоритмам.
Основная операция – сравнение.
Количество основных операций зависит от данных.
Количество основных операций в худшем случае:
То есть алгоритм простой сортировки вставками относится к квадратичному классу эффективности, поэтому он не эффективный для сортировки массивов больших чисел.
· сортировка слиянием
Алгоритм сортировки слиянием относится к рекурсивным алгоритмам.
Основная операция – сравнение.
ВОПРОС: спавнение счит-ся только элементов массива, или любые сравнения в алгоритме?
Количество основных операций зависит от данных.
Рекуррентное уравнение, выражающее количество выполняемых операций сравнения:
То есть алгоритм сортировки слиянием относится к классу эффективности 
, он является не эффективным для массивов малой размерности, и наоборот эффективный для больших массивов.
· быстрая сортировка
Алгоритм быстрой сортировки относится к рекурсивным алгоритмам.
Основная операция – сравнение.
Количество основных операций зависит от данных.
Рекуррентное уравнение, выражающее количество выполняемых операций сравнения:
То есть алгоритм быстрой сортировки относится к классу эффективности , он является не эффективным для массивов малой размерности, и наоборот эффективный для больших массивов.
4.Сравнение производительностей алгоритмов для массивов из элементов по количеству размеров и сравнений. Рассмотреть 3 случая.
Для каждого примера рассмотрим случаи:
а) случайно сгенерированные числа в диапазоне [1..n]
б) последовательность чисел 1, 2, …, n
в) последовательность чисел n, n-1, …,1
· сортировка выбором
Количество сравнений для всех случаев одинаковое, так как для поиска минимального элемента массива алгоритм в любом случае сравнивает все элементы. Для случая отсортированного массива количество обменов равно нулю, поскольку первый элемент уже будет минимальным, и обмен выполняться не будет.
|
|
|
· простая сортировка вставкой
Для случая уже отсортированного массива алгоритм не будет выполнять обмен, поскольку большее число будет всегда стоять справа от меньшего. Для случая массива отсортированного в обратном порядке количество сравнений и обменов наибольшее, так как сравнивать и менять местами необходимо абсолютно каждое число.
· сортировка слиянием
Видим, что для данной сортировки количество обменов всегда равно нулю, так как в алгоритме не выполняется обменов местами элементов массива. А создается буферный массив размера заданного, и, после сравнения элементов 2-х подпоследовательностей, в буферный массив добавляем сначала меньшее число а затем большее.
· быстрая сортировка
Приупорядоченном массиве обменов будет меньше всего, так как элементы меньше среднего числа уже будут стоять слева от него, а больше – справа.
Для массива, отсортированного в обратном порядке, сравнений будет меньше всего, так как при первом же сравнении сразу будут находиться числа, которые нужно поменять местами.
5. Графическое представление полученных данных, вывод на основе их о принадлежности алгоритмов к классам.
· сортировка выбором
· простая сортировка вставкой
По графическим представлениям мы видим, что алгоритмы сортировки выбором и простой сортировки вставкой действительно принадлежат к классам эффективности квадратичной сложности.
· сортировка слиянием
· быстрая сортировка
По графическим представлениям мы видим, что алгоритмы сортировки слиянием и быстрой сортировки действительно принадлежат к классам эффективности .
|
|
|
