 |
Первый алгоритм симплекс-метода
|
|
|
|
Приведём описание алгоритма применительно к ЗЛП, записанной в канонической форме с односторонними ограничениями:

Пусть известен начальный опорный план  с базисом
с базисом  , т.е.
, т.е.  - базисные компоненты,
- базисные компоненты,  - небазисные компоненты.
- небазисные компоненты.
Вычисления удобно выполнять, заполняя следующую симплекс-таблицу:
| C | 
| … | 
| … | 
| ||||
| № | 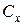
| P | B | 
| … | 
| … | 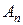
| t |

| 
| 
| 
| … | 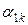
| … | 
| ||
| … | … | … | … | … | … | … | … | … | |

| 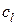
| 
| 
| 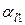
| … | … | 
| 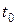
| |
| … | … | … | … | … | … | … | … | … | |
| m | 
| 
| 
| 
| … | 
| … | 
| |

| 
| 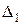
| … | 
| … | 
|
Порядок вычислений по первому алгоритму:
Шаг 1. Найти обратную к  матрицу
матрицу  .
.
Шаг 2. Вычислить коэффициенты разложения векторов условий 
 по базису
по базису  , используя расчётную формулу:
, используя расчётную формулу:

и заполнить ими столбцы  симплекс-таблицы нулевой итерации.
симплекс-таблицы нулевой итерации.
Шаг 3. Вычислить значение линейной формы  , как скалярное произведение
, как скалярное произведение  соответствующих столбцов симплекс-таблицы, и значения оценок
соответствующих столбцов симплекс-таблицы, и значения оценок  векторов условий
векторов условий  относительно базиса
относительно базиса  в соответствии с формулой
в соответствии с формулой  как скалярное произведение столбцов
как скалярное произведение столбцов 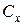 и
и  симплекс-таблицы без коэффициента
симплекс-таблицы без коэффициента  , т.е. по расчётной формуле
, т.е. по расчётной формуле 
Полученными значениями заполнить  строку симплекс-таблицы.
строку симплекс-таблицы.
Шаг 4. Проверить оптимальность опорного плана.
· Если  , то
, то  - оптимальный опорный план и, тогда, в столбце
- оптимальный опорный план и, тогда, в столбце  симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.
· Если хотя бы в одном столбце с отрицательной оценкой 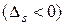 все элементы меньше или равны 0
все элементы меньше или равны 0  , то линейная форма
, то линейная форма  не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
не ограничена сверху и решения ЗЛП не существует. На этом процесс решения ЗЛП также завершается.
|
|
|
· Если же в каждом столбце с отрицательными оценками найдется хотя бы один положительный элемент  , то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки
, то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки  и, таким образом, определяется разрешающий столбец
и, таким образом, определяется разрешающий столбец  .
.
Шаг 5. Определить вектор, исключаемый из базиса для чего необходимо заполнить последний столбец  симплекс-таблицы нулевой итерации путем деления элементов столбца
симплекс-таблицы нулевой итерации путем деления элементов столбца  на соответствующие им по номеру положительные элементы разрешающего столбца
на соответствующие им по номеру положительные элементы разрешающего столбца  , т.е.
, т.е. 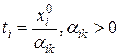 ,
,
При этом, в строках столбца  , соответствующих неположительным элементам
, соответствующих неположительным элементам 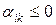 , записываем
, записываем  , не выполняя деления.
, не выполняя деления.
Далее необходимо выбрать  . Если
. Если 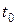 достигается на нескольких позициях столбца
достигается на нескольких позициях столбца  , то из базиса может быть исключен любой из векторов
, то из базиса может быть исключен любой из векторов  . Для определенности, договоримся исключать из них вектор с наименьшим номером.
. Для определенности, договоримся исключать из них вектор с наименьшим номером.
Пусть 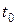 получился на
получился на  -той позиции, т.е.
-той позиции, т.е.  , тогда соответствующий этому индексу вектор
, тогда соответствующий этому индексу вектор  должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент
должен выводиться из базиса. Строка симплекс-таблицы, соответствующая этому индексу, называется разрешающей строкой. Элемент  , стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
, стоящий на пересечении разрешающей строки и разрешающего столбца называется разрешающим элементом. На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.
Шаг 6. Заполнить новую симплекс-таблицу в следующей последовательности.
· На  -тых позициях столбцов
-тых позициях столбцов 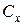 и
и 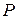 записать соответственно
записать соответственно  и
и  , а на остальных позициях этих столбцов оставить прежние элементы.
, а на остальных позициях этих столбцов оставить прежние элементы.
· Заполнить  -тую строку новой симплекс-таблицы (в ней теперь стоит Ак) элементами
-тую строку новой симплекс-таблицы (в ней теперь стоит Ак) элементами  , получающимися делением соответствующих элементов (
, получающимися делением соответствующих элементов ( )
)  -той строки старой симплекс-таблицы на разрешающий элемент
-той строки старой симплекс-таблицы на разрешающий элемент  , т.е. по формулам
, т.е. по формулам 
· Все остальные  -тые строки главной части новой симплекс-таблицы получить как результат вычитания из
-тые строки главной части новой симплекс-таблицы получить как результат вычитания из  -той строки старой симплекс-таблицы
-той строки старой симплекс-таблицы  -той строки новой симплекс-таблицы, умноженной на соответствующий
-той строки новой симплекс-таблицы, умноженной на соответствующий  -тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами
-тый элемент разрешающего столбца, т.е. в соответствии с рекуррентными формулами 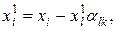

 ,
,  . По аналогичным формулам вычисляются также и элементы
. По аналогичным формулам вычисляются также и элементы  -й строки новой таблицы:
-й строки новой таблицы:  ,
,  ,
,  .
.
|
|
|
Этим завершается построение новой симплекс-таблицы.
Описанный процесс построения симплекс-таблиц повторяется до получения оптимального опорного плана или до установления неограниченности линейной формы, т.е. неразрешимости ЗЛП.
Пример:


Определим начальный опорный план полученной задачи. При постановке этой задачи сформирован единичный базис  искомого начального опорного плана задачи. Его компоненты
искомого начального опорного плана задачи. Его компоненты  являются небазисными и поэтому приравниваются нулю. Тогда из системы ограничений-ограничений найдутся значения базисных компонент
являются небазисными и поэтому приравниваются нулю. Тогда из системы ограничений-ограничений найдутся значения базисных компонент

Итак, в качестве начального опорного плана задачи может быть взят вектор

Решение задачи будем проводить в соответствии с первым алгоритмом симплекс-метода. Составим таблицу, соответствующую исходному опорному плану (0-й итерации). Так как  - базис начального опорного плана
- базис начального опорного плана  , является единичной матрицей, то обратная матрица
, является единичной матрицей, то обратная матрица  также является единичной и поэтому коэффициентами разложения векторов условий
также является единичной и поэтому коэффициентами разложения векторов условий  по этому базису
по этому базису  являются коэффициенты системы ограничений.
являются коэффициенты системы ограничений.
Для заполнения  -й строки симплекс-таблицы вычислим значения линейной формы
-й строки симплекс-таблицы вычислим значения линейной формы  и оценок
и оценок  ,
,  векторов условий
векторов условий  по приведённым в описании первого алгоритма формулам следующим образом:
по приведённым в описании первого алгоритма формулам следующим образом:

Заполняем таблицу 0-й итерации (см. ниже).
Среди оценок  имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису путём операции однократного замещения. В базис будет введён вектор
имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису путём операции однократного замещения. В базис будет введён вектор 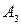 с наименьшей оценкой
с наименьшей оценкой 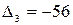 . Значения t вычисляются для всех позиций столбца t (так как все элементы разрешающего столбца положительны). Наименьший элемент
. Значения t вычисляются для всех позиций столбца t (так как все элементы разрешающего столбца положительны). Наименьший элемент 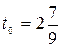 достигается на четвертой позиции базиса. Значит, четвертая строка является разрешающей строкой, и вектор
достигается на четвертой позиции базиса. Значит, четвертая строка является разрешающей строкой, и вектор  подлежит исключению из базиса. Разрешающий элемент – элемент (4;3), равный 18.
подлежит исключению из базиса. Разрешающий элемент – элемент (4;3), равный 18.
0 итерация

| ||||||||||||||

| 
| 
| 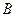
| 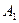
| 
| 
| 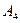
| 
| 
| 
| 
| 
|  
| |

| 25 1/2 | |||||||||||||

| 14 8/9 | |||||||||||||

| 13 1/4 | |||||||||||||

| -1 | 2 7/9 | = 
| |||||||||||
| m+1 | - | - | -30 | -25 | -56 | -48 | - |
|
|
|
1 итерация
Составим таблицу, отвечающую первой итерации.
В столбце P, в четвертой позиции место вектора  займёт вектор
займёт вектор 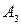 . Соответствующий ему коэффициент линейной формы
. Соответствующий ему коэффициент линейной формы  помещаем в четвертой позиции столбца
помещаем в четвертой позиции столбца  . Затем заполняется строка А3 новой симплекс-таблицы. Для этого все элементы этой строки старой таблицы делятся на разрешающий элемент (на 18).
. Затем заполняется строка А3 новой симплекс-таблицы. Для этого все элементы этой строки старой таблицы делятся на разрешающий элемент (на 18).

| 
| 
| 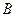
| 
| 
| 
| 
| 
| 
| 
| 
| 
|  
|

| |||||||||||||

| |||||||||||||

| |||||||||||||
| 2 7/9 | 1 1/9 | 7/9 | 1 2/3 | -1/18 | 1/18 | |||||||
| m+1 | - | - |
Все остальные  -тые строки главной части новой симплекс-таблицы получить как результат вычитания из
-тые строки главной части новой симплекс-таблицы получить как результат вычитания из  -той строки старой симплекс-таблицы четвертой строки новой симплекс-таблицы, умноженной на соответствующий
-той строки старой симплекс-таблицы четвертой строки новой симплекс-таблицы, умноженной на соответствующий  -тый элемент разрешающего столбца. Например, определим значение в клетке (1,В):
-тый элемент разрешающего столбца. Например, определим значение в клетке (1,В):

| ||||||||||||

| 
|  
| 
| 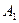
|  
| 
| 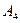
| 
| 
| 
| 
| 
|

| ||||||||||||

|  268 268
|  14 14
| ||||||||||

| ||||||||||||

| -1 | |||||||||||
| m+1 | - | - | -30 | -25 | -56 | -48 |
|
|



| 
| 
| 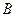
| 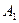
| 
| 
| 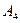
| 
| 
| 
| 
| 
|

| 45 4/9 | |||||||||||

| ||||||||||||
 
| ||||||||||||
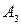
| 2 7/9 | 1 1/9 | 7/9 | 1 2/3 | -1/18 | 1/18 | ||||||
| m+1 | - | - |
И так все свободные ячейки. окончательно вид таблицы на первой итерации:
|
|
|
1 итерация.

| 
| 
| 
| 
| 
| 
| 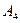
| 
| 
| 
| 
| 
|  
|

| 45 4/9 | 5/9 | 3 4/9 | 2/3 | 1/9 | -1/9 | |||||||

| -1 | ||||||||||||

| 83 7/9 | 2/9 | 7 7/9 | 2 2/3 | 4/9 | -4/9 | 188 1/2 | ||||||
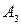
| 2 7/9 | 1 1/9 | 7/9 | 1 2/3 | -1/18 | 1/18 | +∞ | ||||||
| m+1 | - | - | 155 5/9 | 38 4/9 | 18 5/9 | 45 1/3 | -3 1/9 | 3 1/9 | - |
В симплекс-таблице первой итерации также есть отрицательные оценки, поэтому опорный план опять не оптимален. Минимальное отрицательное значение получаем для столбца А8, следовательно, в базис будет введен столбец А8 (А8-разрешающий столбец). При определении разрешающей строки получили, что из базиса будет выведена строка А7.
Таблица второй итерации будет иметь вид:
2 итерация

| 
| 
| 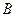
| 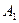
| 
| 
| 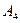
| 
| 
| 
| 
| 
|

| 24 1/2 | 1/2 | 1 1/2 | -1/4 | ||||||||

| 29 1/2 | -1.2 | -17 1/2 | -6 | -2 1/4 | |||||||
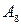
| 188 1/2 | 1.2 | 17 1/2 | 2 1/4 | -1 | |||||||
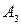
| 13 1/4 | 1 1/4 | 1 3/4 | 1/8 | ||||||||
| m+1 | - | - |
Так как после завершения второй итерации все оценки  , то полученный опорный план
, то полученный опорный план  является оптимальным опорным планом задачи. Максимальное значение линейной формы равно нулю
является оптимальным опорным планом задачи. Максимальное значение линейной формы равно нулю 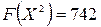 .
.
|
|
|


