 |
Рабочий процесс лопастного насоса
|
|
|
|
В рабочем колесе энергия передается жидкости путем динамического воздействия лопаток на поток. Момент сил относительно оси противодействует вращению рабочего колеса, поэтому лопатки профилируют, учитывая величину подачи, частоту вращения, направление движения жидкости.
Преодолевая момент, рабочее колесо совершает работу. Основная часть, подведенная к колесу энергии, передается жидкости, некоторая часть теряется на преодоление механических и гидравлических сопротивлений.
Если неподвижную систему координат связать с корпусом насоса, а подвижную систему координат с рабочим колесом, то траектория абсолютного движения частиц будет складываться из вращения (переносного движения) рабочего колеса и относительного движения в подвижной системе по лопаткам.
Абсолютная скорость равна векторной сумме переносной скорости - скорости вращения U рабочего колеса и относительной скорости W (по лопатке) в данной точке. На рис. 15.2 изображены траектории частиц на входе и на выходе в насос в относительном движении – АВ, траектории переносного движения совпадают с окружностями на данном радиусах колеса, например на радиусах R1 и R2. Траектории частиц в абсолютном движении от входа в насос до выхода – АС. Движение подвижной системы –относительное, в подвижной – переносное.
Параллелограммы скоростей для входа в рабочее колесо и выхода из него:
 (15.5’)
(15.5’)
где i = 1,2.
Отложив относительную скорость W2 с переносной U2, получим абсолютную скорость V2 на выходе из рабочего колеса.

Из параллелограммов скоростей, изображенных на рис. 15.2, видно, что момент скорости частицы жидкости на выходе из рабочего колеса больше, чем на входе:
V2Cosα2R2 > V1Cosα1R1
|
|
|
Следовательно, при прохождении через колесо момент количества движения увеличивается. Возрастание момента количества движения вызвано моментом сил, с которыми рабочее колесо действует на находящуюся в нем жидкость.
Для установившегося движения жидкости разность моментов количества движения жидкости, выходящей из канала и входящей в него за единицу времени, равна моменту внешних сил, с которыми рабочее колесо действует на жидкость. Поэтому момент сил, с которыми рабочее колесо действует на жидкость, равен:
М = Qρ(V2Cosα2R2 - V1Cosα1R1),
где Q - расход жидкости через рабочее колесо.
Умножим обе части этого уравнения на угловую скорость рабочего колеса ω.
М ω= Qρ(V2Cosα2R2ω - V1Cosα1R1ω),
Произведение Мω называется гидравлической мощностью, или работой которую производит рабочее колесо в единицу времени, воздействуя на находящуюся в нем жидкость.
Из уравнения Бернулли известно, что удельная энергия, передаваемая единице веса жидкости, называется напором. Когда нами изучалось уравнение Бернулли, источником энергии для движения жидкости была разность напоров.
В данном случае энергия передается жидкости рабочим колесом насоса.
Теоретическим напором рабочего колеса - НТ называется удельная энергия, передаваемая единице веса жидкости рабочим колесом насоса.
N = Мω = HТ*Qρg
Учитывая, что u1=R1ω — переносная (окружная) скорость рабочего колеса на входе и u2 = R2 ω — скорость рабочего колеса на выходе и что проекции векторов абсолютных скоростей на направление переносной скорости (перпендикулярной к радиусам R1 и R2) равны Vu2 =V2Cosα2 и Vu1 = V1Cosα1, где Vu2 и Vu1 , получим теоретический напор в виде
HТ*Qρg = Qρ(V2Cosα2R2ω - V1Cosα1R1ω),
 (15.6)
(15.6)
Напор насоса  меньше теоретического напора поскольку в нем взяты реальные значения скоростей и давлений.
меньше теоретического напора поскольку в нем взяты реальные значения скоростей и давлений.
Лопастные насосы бывают одноступенчатыми и многоступенчатыми. В одноступенчатых насосах жидкость проходит через рабочее колесо однократно (см. рис. 14.1). Напор таких насосов при заданной частоте вращения ограничен. Для повышения напора применяют многоступенчатые насосы, у которых имеется несколько последовательно соединенных рабочих колес, закрепленных на одном валу. Напор насоса повышается пропорционально числу колес.
|
|
|
Лопастной насос может работать при разных режимах, т. е. при разных подачах и частотах вращения.
Прикрывая задвижку, установленную на напорном трубопроводе насоса, уменьшают подачу. При этом также изменяется напор, развиваемый насосом. Для правильной эксплуатации насоса необходимо знать, как изменяется напор, КПД и мощность, потребляемая насосом, при изменении его подачи, т. е. знать характеристику насоса, под которой понимается зависимость напора, мощности и КПД насоса от его подачи при постоянной частоте вращения
 |
1. 42___ Основное уравнение лопастных насосов.
Основное уравнение центробежного насоса впервые в самом общем виде было получено в 1754 г. Л. Эйлером и носит ею имя.
Рассматривая движение жидкости внутри рабочего колеса, сделаем следующие допущения: насос перекачивает идеальную жидкость в виде струй, т. е. в насосе отсутствуют все виды потерь энергии. Число одинаковых лопастей насоса бесконечно большое (z = µ), толщина их равна нулю (d= 0), а угловая скорость вращения колеса постоянна (w= const.).
К рабочему колесу центробежного насоса со скоростью Vo жидкость подводится аксиально, т. е. в направлении оси вала. Затем направление струй жидкости изменяется от осевого до радиального, перпендикулярного оси вала, а скорость благодаря центробежной силе увеличивается от значения V1 в пространстве между лопастями рабочего колеса до значения V2 на выходе из колеса.
В межлопастном пространстве рабочего колеса при движении жидкости различают абсолютную и относительную скорости потока. Относительная скорость потока — скорость относительно рабочего колеса, а абсолютная — относительно корпуса насоса.


Рис. Схема движения жидкости в рабочем колесе центробежного насоса
Абсолютная скорость равна геометрической сумме относительной скорости жидкости и окружной скорости рабочего колеса. Окружная скорость жидкости, выходящей между лопастями рабочего колеса, совпадает с окружной скоростью колеса в данной точке.
|
|
|
Окружная скорость жидкости (м/с) на входе в рабочее колесо
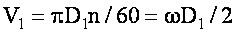
где n—частота вращения рабочего колеса, об/мин; D1 и D2 — внутренний и внешний диаметры рабочего колеса, м, w— угловая скорость вращения рабочего колеса рад/с
При движении рабочего колеса частицы жидкости движутся вдоль лопастей. Вращаясь вместе с рабочим колесом, они приобретают окружную скорость, а перемещаясь вдоль лопастей — относительную.
Абсолютная скорость v движения жидкости равна геометрической сумме ее составляющих: относительной скорости w и окружной u, т. е. v = w + и.
Связь между скоростями частиц жидкости выражается параллелограммом или треугольниками скоростей, что позволяет дать понятие о радиальной и окружной составляющих абсолютной скорости.
Радиальная составляющая

окружная составляющая

где a— угол между абсолютной и окружной скоростями (на входе рабочего колеса a1 и на выходе a2).
Угол b между относительной и окружной скоростями характеризует очертание лопастей насоса.
Исследуем изменение за 1 с момента количества движения Массы жидкости т = rQ, где r — плотность жидкости; Q— подача насоса.
Используя теорему механики об изменении моментов количества движения применительно к движению жидкости в канале рабочего колеса, выведем основное уравнение центробежного насоса, которое позволит определить развиваемый насосом напор (или давление). Эта теорема гласит: изменение во времени главного момента количества движения системы материальных точек относительно некоторой оси равно сумме моментов всех сил, действующих на эту систему.
Момент количества движения жидкости относительно оси рабочего колеса во входном сечении

Момент количества движения на выходе из рабочего колеси
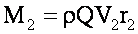
где r1 и r2 — расстояния от оси колеса до векторов входной V1 и выходной V2 скоростей соответственно.
Согласно определению момента системы можно записать:
|
|
|

Так как в соответствии с рис

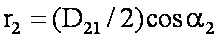

Группы внешних сил — силы тяжести, силы давления в расчетных сечениях (входа-выхода) и со стороны рабочего колеса и силы трения жидкости на обтекаемых поверхностях лопастей рабочего колеса — действуют на массу жидкости, заполняющей межлопастные каналы рабочего колеса.
Момент сил тяжести относительно оси вращения всегда равен нулю, так как плечо этих сил равно нулю. Момент сил давления в расчетных сечениях по этой же причине также равен нулю. Если силами трения пренебрегают, то и момент сил трения равен нулю. Тогда момент всех внешних сил относительно оси вращения колеса сводится к моменту Мк динамического воздействия рабочего колеса на протекающую через него жидкость, т. е.

Произведение Мк на относительную скорость равно произведению расхода на теоретическое давление PT, создаваемое насосом, т. е. равно мощности, передаваемой жидкости рабочим колесом. Следовательно,

Это уравнение можно представить в виде
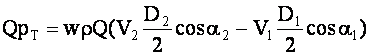
Разделив обе его части на Q, получим

Учитывая, что напор Н = Р/(pg) и подставив это значение получим

Если пренебречь силами трения, то можно получить зависимости, называемые основными уравнениями лопастного насоса. Эти уравнения отражают зависимость теоретического давления или напора от основных параметров рабочего колеса. Переносные скорости на входе в осевой насос и на выходе из него |одинаковы, поэтому уравнение принимает вид

В большинстве насосов жидкость в рабочее колесо поступает практически радиально и, следовательно, скорость V1» 0. C учетом вышеизложенного
 или
или 
Теоретические давление и напор, развиваемые насосом, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса, т. е. чем больше его диаметр, частота вращения и угол b2, т. е. чем «круче» расположены лопатки рабочего колеса.
Действительные давление и напор, развиваемые насосом, меньше теоретических, так как реальные условия работы насоса отличаются от идеальных, принятых при выводе уравнения. Давление, развиваемое насосом, уменьшается главным образом из-за того, что при конечном числе лопастей рабочего колеса не все частицы жидкости отклоняются равномерно, вследствие чего уменьшается абсолютная скорость. Кроме того, часть энергии расходуется на преодоление гидравлических сопротивлении. Влияние конечного числа лопастей учитывают введением поправочного коэффициента k (характеризующею уменьшение окружной составляющей скорости V2u), уменьшение давления вследствие гидравлических потерь — введением гидравлического коэффициента полезного действия hr. С учетом этих поправок полное давление
|
|
|
 а полный напор
а полный напор 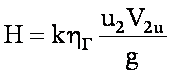
Значение коэффициента hr зависит от конструкции насоса, его размеров и качества выполнения внутренних поверхностей проточной части колеса. Обычно значение hr составляет 0,8...0,95. Значение k при числе лопастей от 6 до 10, a2 = 8...140 и V2u = 1,5...4 м/с колеблется от 0,75 до 0,9.
При вращении рабочего колеса центробежного насоса жидкость, находящаяся между лопатками, благодаря развиваемой центробежной силе выбрасывается через спиральную камеру в напорный трубопровод. Уходящая жидкость освобождает занимаемое ею пространство в каналах на внутренней окружности рабочего колеса, поэтому у входа в рабочее колесо образуется вакуум, а на периферии — избыточное давление. Под действием разности атмосферного давления в приемном резервуаре и пониженного давления на входе в рабочее колесо жидкость по всасывающему водопроводу поступает в межлопаточные каналы рабочего колеса.
Центробежный насос может работать только в том случае, когда его внутренняя полость заполнена перекачиваемой жидкостью не ниже оси насоса, поэтому насосную установку оборудуют устройством для залива насоса.
|
|
|


