 |
Оценка параметров распределения
|
|
|
|
42,02; 56,45; 58,61; 28,69; 57,43; 25,95; 36,51; 46,81; 46,61; 52,28; 50,94; 38,55; 63,98; 64,26; 78,09; 48,94; 44,41; 22,93; 42,24; 39,79; 35,98; 57,46; 13,22; 47,91; 50,33; 69,37; 46,57; 63,13; 58,75; 41,36; 23,75; 36,42; 45,19; 43,15; 61,76; 55,28; 57,60; 54,91; 47,73; 60,69; 66,35; 47,93; 38,90; 38,61; 40,51; 49,11; 63,35; 44,72; 53,95; 50,42
Выполнить следующие задания:
1. Построить вариационный ряд.
2. Составить статистический ряд по вариационному ряду
3. П остроить полигон и гистограмму частот.
4. Найти числовые характеристики.
5. Найти доверительный интервал с надежностью  =0,95 для неизвестного математического ожидания (оцениваемый параметр нормального распределения) по выборочному среднему при известном среднем квадратическом отклонении.(в конце лекции)
=0,95 для неизвестного математического ожидания (оцениваемый параметр нормального распределения) по выборочному среднему при известном среднем квадратическом отклонении.(в конце лекции)
6. Проверить гипотезу при уровне значимости  , если предположить, что количественный признак генеральной совокупности распределен нормально.(в конце лекции)
, если предположить, что количественный признак генеральной совокупности распределен нормально.(в конце лекции)
Решение.
1.
13,22; 22,93; 23,75; 25,95; 28,69; 35,98; 36,42; 36,51; 38,55; 38,61; 38,90; 39,79; 40,51; 41,36; 42,02; 42,24; 43,15; 44,41; 44,72; 45,19; 46,57; 46,61; 46,81; 47,73; 47,91; 47,93; 48,94; 49,11; 50,33; 50,42; 50,94; 52,28; 53,95; 54,91; 55,28; 56,45; 57,43; 57,46; 57,60; 58,61; 58,75; 60,69; 61,76; 63,13; 63,35; 63,98; 64,26; 66,35; 69,37; 78,09.
2. Найдем длины частичных промежутков. Поскольку  ,
,  ,
,  (округляем до ближайшего целого числа), то
(округляем до ближайшего целого числа), то  (округляем с избытком).
(округляем с избытком).
| Промежуток | 
| 
| 
| 
| 
| 
| 
|

|
Контроль:  .
.
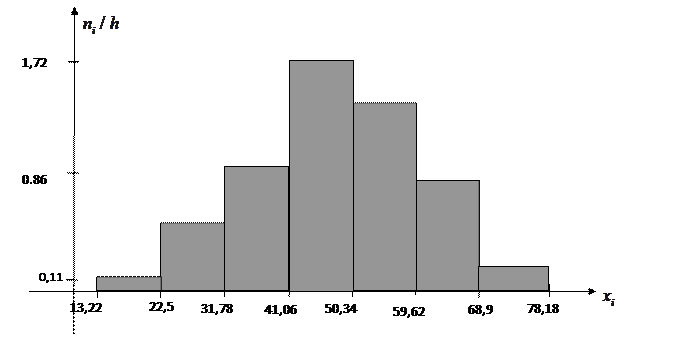
3. По статистическому ряду построим полигон и гистограмму.
Гистограмма применяется для графической интерпретации статистического ряда непрерывной случайной величины, а полигон для статистического ряда дискретной случайной величины. (ПОЛИГОН ДЛЯ НАШЕГО ПРИМЕРА СПРАВА, ЛЕВЫЙ ПОЛИГОН ЛИШНИЙ, ОН К ДРУГОМУ ПРИМЕРУ, НА НЕГО НЕ СМОТРЕТЬ)

Если взять для каждого из частичных промежутков его середину, то статистический ряд можно переписать в том виде, который позволяет построить полигон для данного непрерывного признака.
|
|
|

| 17,86 | 27,14 | 36,42 | 45,7 | 54,98 | 64,26 | 73,54 |

|
Для построения гистограммы по статистическому ряду составим следующую таблицу (число  было найдено выше):
было найдено выше):
| Промежуток | 
| 
| 
| 
| 
| 
| 
|

| |||||||

| 0,11 | 0,43 | 0,86 | 1,72 | 1,29 | 0,75 | 0,22 |
4. Найдем числовые характеристики.
Вычислим выборочное средние:
 .
.
Вычислим дисперсию:
 Вычислим среднее квадратическое отклонения:
Вычислим среднее квадратическое отклонения:  .
.
Найдем теперь асимметрию и эксцесс, используя соответствующие определения:
;  . Замечание.
. Замечание.
Отрицательная асимметрия означает, что кривая плотности распределения, построенная по эмпирическим данным, является более пологой слева. Положительная асимметрия означает, что такая кривая более пологая справа.
Эксцесс позволяет сравнить данную кривую с кривой нормального распределения, для которой он равен 3. Если эксцесс (показатель островершинности) положителен, то данная кривая будет выше кривой нормального распределения, а в противном случае, ниже.
Для графической интерпретации этих соотношений следует использовать стандартизованные величины, т.е. математические ожидания и средние квадратические отклонения сравниваемых распределений должны быть равны соответственно нулю и единице (сравнивать можно только «одинаковые» объекты).
ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Если в теории вероятностей для заданного вида распределения параметры определяются однозначно, то в математической статистике такие параметры являются случайными, они вычисляются по выборочным значениям, которые меняются от одной выборки к другой. Поэтому такие случайные значения параметров называют их точечными оценками, т.е. оценками, которые характеризуют искомый параметр одним числом.
Опр. Статистической оценкой  параметра
параметра  теоретического распределения (т.е. распределения количественного признака генеральной совокупности) называют его приближенное значение, зависящее от выборки:
теоретического распределения (т.е. распределения количественного признака генеральной совокупности) называют его приближенное значение, зависящее от выборки:  . Функцию результатов наблюдений называют статистикой.
. Функцию результатов наблюдений называют статистикой.
|
|
|
Замечание. Если число наблюдений мало, то замена искомого параметра его оценкой, например математического ожидания средним арифметическим, приводит к ошибке. По этой причине, и некоторым другим, к оценке любого параметра предъявляется ряд требований, которым должна удовлетворять оценка хорошего качества, а именно: несмещенность, состоятельность и эффективность. Требование несмещенности указывает на отсутствие систематической ошибки. Требование состоятельности предполагает, что оценка приближается к истинному значению параметра с ростом числа наблюдений.
Замечание. На практике не всегда удается подобрать оценки, удовлетворяющие всем трем критериям.
Рассмотрим далее точечные оценки математического ожидания, т.е. оценку будем вычислять по выборке.
Пусть 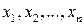 − выборка, полученная в результате проведения
− выборка, полученная в результате проведения  независимых наблюдений за случайной величиной
независимых наблюдений за случайной величиной  . Представим значения
. Представим значения 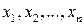 как набор значений случайных величин
как набор значений случайных величин  , т.е. под
, т.е. под  будем понимать значение случайной величины
будем понимать значение случайной величины  в
в  -ом наблюдении.
-ом наблюдении.
Эти случайные величины можно рассматривать как  независимых случайных величин. Поэтому
независимых случайных величин. Поэтому  .
.
Теорема. Если  − выборка из генеральной совокупности и
− выборка из генеральной совокупности и  , то выборочное среднее
, то выборочное среднее  − несмещенная и состоятельная оценка математического ожидания
− несмещенная и состоятельная оценка математического ожидания  .
.
Замечание. Относительная частота ( ) появления случайного события
) появления случайного события 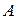 в
в  независимых наблюдениях является несмещенной, состоятельной и эффективной оценкой вероятности этого события (
независимых наблюдениях является несмещенной, состоятельной и эффективной оценкой вероятности этого события ( ).
).
В случае, когда объем выборки невелик, точечные оценки приводят к ошибкам, т.к. дают большую погрешность. Этого недостатка лишены интервальные оценки неизвестного параметра  , т.е. те, которые определяются концами интервала.
, т.е. те, которые определяются концами интервала.
Опр. Интервал  , покрывающий с вероятностью
, покрывающий с вероятностью  истинное значение параметра
истинное значение параметра  , называется доверительным интервалом, а число
, называется доверительным интервалом, а число  − надежностью оценки или доверительной вероятностью.
− надежностью оценки или доверительной вероятностью.
Чаще всего доверительный интервал выбирают симметричным относительно несмещенной точечной оценки параметра  , т.е.
, т.е.  , где число
, где число 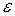 характеризует точность оценки.
характеризует точность оценки.
|
|
|
Надежность принято выбирать равной 0,9; 0,95; 0,99; 0,999, т.е. когда почти достоверно, что доверительный интервал покрывает оцениваемый параметр.
Рассмотрим интервальную оценку для математического ожидания нормального распределения.
Пусть 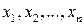 − выборка, полученная в результате проведения
− выборка, полученная в результате проведения  независимых наблюдений за случайной величиной
независимых наблюдений за случайной величиной  , для которой известно среднее квадратическое отклонение
, для которой известно среднее квадратическое отклонение  . Зададим доверительную вероятность равной
. Зададим доверительную вероятность равной  . Оценкой математического ожидания является выборочное среднее
. Оценкой математического ожидания является выборочное среднее 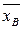 , которое, как и сама величина
, которое, как и сама величина  , распределено по нормальному закону.
, распределено по нормальному закону.
Рассмотрим случайную величину 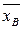 . Определим параметры её распределения:
. Определим параметры её распределения:
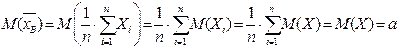 ,
, 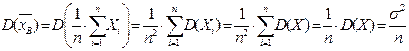 .
.
Используем формулу теории вероятностей вероятности попадания в интервал для нормально распределенной случайной величины:  . Тогда для случайной величины
. Тогда для случайной величины 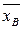 имеем:
имеем:  , где
, где  . Из последнего равенства находим
. Из последнего равенства находим  , (из этой формулы следует, что с возрастанием объема выборки точность оценки увеличивается, а увеличение надежности уменьшает точность оценки), следовательно
, (из этой формулы следует, что с возрастанием объема выборки точность оценки увеличивается, а увеличение надежности уменьшает точность оценки), следовательно 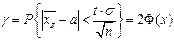 . Таким образом, интервал
. Таким образом, интервал 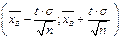 - доверительный интервал для
- доверительный интервал для  . Поскольку
. Поскольку  было задано, то по таблице значений функции Лапласа из равенства
было задано, то по таблице значений функции Лапласа из равенства  находим аргумент t.
находим аргумент t.
Пример. Найти доверительный интервал с надежностью  =0,95 для неизвестного математического ожидания (оцениваемый параметр нормального распределения) по выборочному среднему при известном среднем квадратическом отклонении, если выборочное среднее
=0,95 для неизвестного математического ожидания (оцениваемый параметр нормального распределения) по выборочному среднему при известном среднем квадратическом отклонении, если выборочное среднее  = 48,11, среднее квадратическое отклонение
= 48,11, среднее квадратическое отклонение  = 12,29 и объем выборки
= 12,29 и объем выборки  = 50.
= 50.
Решение.
Воспользуемся подходящей формулой  . Из уравнения
. Из уравнения  или
или  по таблице находим
по таблице находим  = 1,96. Точность равна
= 1,96. Точность равна  . Следовательно, доверительный интервал для неизвестного математического ожидания при известном
. Следовательно, доверительный интервал для неизвестного математического ожидания при известном  имеет вид
имеет вид  или
или 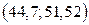 . Этот интервал с вероятностью 0,95 покрывает математическое ожидание.
. Этот интервал с вероятностью 0,95 покрывает математическое ожидание.
|
|
|


