 |
Некоторые математические формулы
|
|
|
|
Содержание
Введение……………………………………………………………….. 4
Требования к оформлению контрольной работы…………………… 5
Задания к контрольной работе.……………………………………… 6
Образцы решения и оформления задач…………………….……….. 17
Литература…………………………………………………………….. 45
Приложение А Некоторые математические формулы…...…………. 46
Приложение Б Схема исследования функции…...………………..... 49
Введение
Одним из важнейших направлений развития современной высшей школы является совершенствование системы специальной подготовки будущих специалистов. В связи с этим в работе со студентами заочного факультета главным средством обучения является систематическая самостоятельная работа во внеаудиторное время. Поэтому обязательным элементом учебного процесса является выполнение письменных контрольных работ.
Контрольная работа в системе заочного обучения является одной из форм активизации самостоятельной работы студентов в межсессионный период, ее подготовка требует от студента самостоятельного изучения научной и учебной литературы. В соответствии с учебным планом студенты заочного факультета специальности «Математика» выполняют контрольную работу по разделам «Предел. Непрерывность. Дифференцируемость» математического анализа.
Цель выполнения контрольной работы по математическому анализу состоит в закреплении и углублении теоретических знаний по изучаемой дисциплине, приобретении практических навыков в решении задач, развитии навыков самостоятельной работы по применению теории к решению задач.
При подготовке контрольной работы студент должен продемонстрировать знание материала, умение правильно и четко излагать свою мысль. При возникновении затруднений у студента в процессе контрольной работы следует обратиться за консультацией к преподавателю на кафедру математического анализа.
|
|
|
Выполнение контрольной работы осуществляется по вариантам.
Требования к оформлению контрольной работы
К оформлению контрольной работы предъявляются следующие требования. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
1 Контрольную работу следует выполнять в отдельной тетради, оставляя поля для замечаний рецензента.
2 Контрольная работа включает в себя следующие структурные элементы:
− титульный лист;
− основную часть, которая представляется заданием по соответствующему варианту темы контрольной работы;
− приложения (если есть);
− список использованной литературы.
3 На титульном листе указывается наименование дисциплины, номер варианта, факультет, курс и номер группы, фамилия и инициалы студента. Вариант определяется в соответствии с последней цифрой в номере зачетной книжки студента.
4 В работу должны быть включены все задачи выполняемого варианта. Контрольные работы, содержащие не все задания или задания не своего варианта, не засчитываются.
5 Решения задач надо располагать в порядке следования номеров. Перед решением каждой задачи должно быть полностью выписано ее условие. Решения задач должны сопровождаться краткими пояснениями и необходимыми чертежами.
6 Выполненная и оформленная в соответствии с требованиями работа подписывается студентом с указанием даты ее выполнения.
7 Студент должен представить контрольную работу на рецензирование не позже установленного графиком учебного процесса срока.
Рецензирование и защита контрольной работы проводится в соответствии с «Положением о контрольной работе студента заочного факультета и порядке ее рецензирования» от 23 февраля 2005 года.
|
|
|
Все сделанные рецензентом замечания студент обязан учесть и внести в работу необходимые исправления и дополнения.
8 Студенты, не получившие зачета по контрольной работе, к экзамену по соответствующей дисциплине не допускаются.
Образцы решения и оформления задач
Задание 1
Используя метод математической индукции, доказать, что верно следующее утверждение.
Пример 1 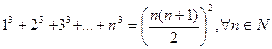 .
.
Решение
1 При 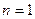 равенство верно, так как
равенство верно, так как  .
.
2 Допустим, что равенство верно при  , т. е.
, т. е.
 .
.
3 Докажем, что равенство верно при  .
.
Рассмотрим

 .
.
Это означает, что при  равенство верно. В силу принципа математической индукции, утверждение верно для
равенство верно. В силу принципа математической индукции, утверждение верно для 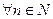 .
.
Пример 2 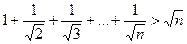 ,
,  .
.
Решение
1 Проверим утверждение при  :
:  .
.
Умножив обе части неравенства на  , получим равносильное неравенство
, получим равносильное неравенство
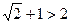 , т. е.
, т. е.  .
.
Так как последнее неравенство верно, то при  данное утверждение верно.
данное утверждение верно.
2 Допустим, что неравенство верно при  , т. е.
, т. е.
 (1)
(1)
3 Докажем, что неравенство верно при  , т. е. докажем, что
, т. е. докажем, что
 .
.
Прибавим  к обеим частям неравенства (1), получим
к обеим частям неравенства (1), получим

Утверждение доказано для  , а в силу принципа математической индукции, и для
, а в силу принципа математической индукции, и для 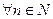 .
.
Пример 3  кратно 133,
кратно 133, 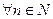 .
.
Решение
1 При 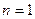 утверждение верно, так как
утверждение верно, так как  делится на 133.
делится на 133.
2 Допустим, что утверждение верно при  , т. е. что
, т. е. что 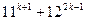 кратно 133.
кратно 133.
3 Докажем, что утверждение верно при  , т. е. что
, т. е. что
 кратно 133.
кратно 133.
Преобразуем 
 .
.
Первое слагаемое кратно 133 по предположению, второе, очевидно, кратно 133. Следовательно, сумма кратна 133. Утверждение доказано.
Задание 2
Преобразовать десятичную периодическую дробь 3,(15) в обыкновенную дробь.
Решение Заметим, что данную дробь можно представить в виде суммы членов бесконечно убывающей геометрической прогрессии:


 .
.
Итак,  .
.
Задание 3
Доказать ограниченность множества А. Найти его точные верхнюю и нижнюю грани, если  .
.
Решение Так как 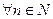 выполняется неравенство
выполняется неравенство  ,
,
то множество А является ограниченным.
Запишем каждый элемент множества А в виде:
 .
.
Таким образом,  .
.
Очевидно, множество А имеет минимальный элемент 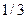 . Тогда
. Тогда
 .
.
Максимального элемента множество А не имеет. Но поскольку множество А ограничено, то оно имеет точную верхнюю грань.
|
|
|
Докажем, что  . Действительно,
. Действительно, 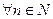 имеем
имеем
 .
.
Значит, число  является верхней гранью.
является верхней гранью.
Возьмем теперь  и покажем, что число
и покажем, что число  не является верхней гранью множества А, т. е. что
не является верхней гранью множества А, т. е. что  такое, что
такое, что  .
.
Найдем какие-либо решения этого неравенства. Оно равносильно неравенству 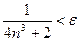 . Но если
. Но если 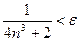 , то
, то  ,
, 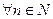 . Отсюда
. Отсюда
 , т. е.
, т. е. 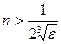 .
.
Итак, при 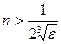 элементы множества А оказываются больше, чем
элементы множества А оказываются больше, чем  . Значит,
. Значит,  число
число  не является верхней гранью множества А. Тем самым доказано, что
не является верхней гранью множества А. Тем самым доказано, что 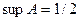 .
.
Задание 4
Для каждого  определить номер
определить номер  такой, что для каждого
такой, что для каждого  выполняется неравенство
выполняется неравенство 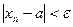 .
.
Пример 1 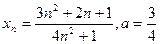 .
.
Решение Возьмем произвольное число  . Рассмотрим модуль разности
. Рассмотрим модуль разности

 .
.
Неравенство  будет выполняться, если
будет выполняться, если  , т. е. при
, т. е. при 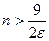 .
.
Возьмем в качестве искомого  число
число  . Тогда
. Тогда 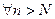 будет выполнено
будет выполнено  .
.
Итак, доказано, что 

 .
.
Пример 2  ,
,  .
.
Решение Возьмем произвольное число  . Рассмотрим модуль разности
. Рассмотрим модуль разности 
 .
.
Неравенство 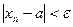 будет выполнено, если
будет выполнено, если  , т. е. при
, т. е. при  . Возьмем в качестве
. Возьмем в качестве  число
число  . Тогда
. Тогда 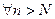 будет выполняться неравенство
будет выполняться неравенство 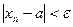 .
.
Таким образом, доказано, что 
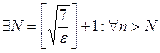
 .
.
Задание 5
Пользуясь теоремой о пределе подпоследовательности, доказать расходимость данной последовательности.
Пример 1  .
.
Указание Известно, что если последовательность имеет предел, то все ее подпоследовательности имеют тот же предел. Следовательно, для доказательства расходимости достаточно найти две подпоследовательности, имеющие различные пределы, или хотя бы одну подпоследовательность, не имеющую конечного предела.
Решение Рассмотрим две подпоследовательности (при четных и нечетных номерах n).
Если n – четное, то  .
.
Если n – нечетное, то  .
.
Так как данная последовательность имеет две подпоследовательности, имеющие различные пределы, то она расходится.
Пример 2  .
.
Решение Возьмем  , тогда
, тогда  . Но тогда
. Но тогда  . Получили подпоследовательность, которая не является ограниченной. Вследствие теоремы об ограниченности сходящейся последовательности, неограниченная последовательность расходится. Следовательно, и
. Получили подпоследовательность, которая не является ограниченной. Вследствие теоремы об ограниченности сходящейся последовательности, неограниченная последовательность расходится. Следовательно, и  – расходится.
– расходится.
Пример 3 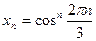 .
.
Решение Возьмем  . Тогда
. Тогда  .
.
|
|
|
Теперь возьмем  , тогда
, тогда
 .
.
Первая подпоследовательность состоит из единиц, а значит, сходится к 1. Так как  при
при 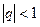 , то вторая подпоследовательность сходится к 0.
, то вторая подпоследовательность сходится к 0.
Следовательно, данная последовательность расходится.
Задание 6
Пример 1 Пользуясь теоремой о произведении бесконечно малой последовательности на ограниченную последовательность, доказать сходимость следующей последовательности:
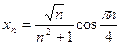 .
.
Решение Последовательность  является бесконечно малой, так как
является бесконечно малой, так как 
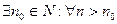

(действительно, в качестве 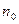 можно взять число
можно взять число 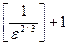 ).
).
Так как 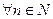
 , то последовательность
, то последовательность 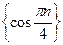 – ограничена.
– ограничена.
Так как последовательность  представляет собой произведение бесконечно малой последовательности на ограниченную последовательность, то она сходится.
представляет собой произведение бесконечно малой последовательности на ограниченную последовательность, то она сходится.
Пример 2 Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость следующей последовательности.
 , где
, где 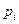
 – целые неотрицательные числа, не превосходящие 9.
– целые неотрицательные числа, не превосходящие 9.
Решение Так как 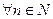
 , то
, то 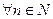
 , т. е. данная последовательность возрастает.
, т. е. данная последовательность возрастает.
Докажем теперь, что она ограничена сверху.

 .
.
Итак, 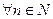
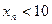 . Значит,
. Значит,  ограничена сверху.
ограничена сверху.
По теореме о существовании предела монотонной и ограниченной последовательности,  сходится.
сходится.
Задание 7
Вычислить пределы последовательностей.
Пример 1 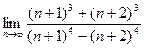 .
.
Решение Преобразуем выражение под знаком предела по формулам
 ,
,
 .
.
Тогда 
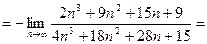 [разделим числитель и знаменатель на
[разделим числитель и знаменатель на  ]
] 
 .
.
Здесь мы воспользовались тем, что  , и арифметическими свойствами пределов.
, и арифметическими свойствами пределов.
Примечание В дальнейшем при вычислении подобных пределов можно использовать правило: при  предел отношения многочленов одинаковых степеней равен отношению коэффициентов при старших степенях n.
предел отношения многочленов одинаковых степеней равен отношению коэффициентов при старших степенях n.
Пример 2  .
.
Решение Умножим и разделим выражение под знаком предела на сопряженное выражение, т. е. на  . Получим
. Получим
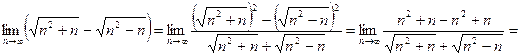
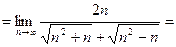 [разделим числитель и знаменатель на n ]
[разделим числитель и знаменатель на n ] 
 .
.
Пример 3  .
.
Решение Умножим и разделим выражение под знаком предела на неполный квадрат соответствующей суммы, т. е. на
 .
.
Получим 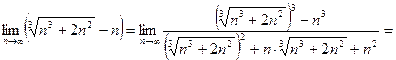
 [разделим числитель и знаменатель на
[разделим числитель и знаменатель на  ]
] 
 .
.
Пример 4  .
.
Решение Умножим и разделим выражение под знаком предела на
 .
.
Получим 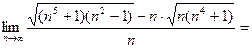


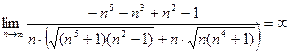 .
.
Здесь мы воспользовались тем, что старшая степень числителя (5) больше старшей степени знаменателя (4,5).
Пример 5 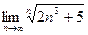 .
.
Решение Воспользуемся теоремой о промежуточной последовательности и табличными пределами (Приложение А):
 ,
,  .
.
Докажем, что данный предел тоже равен 1. Воспользуемся оценками
 ,
,
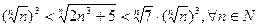 .
.
Так как 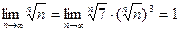 , то
, то  .
.
Пример 6  .
.
Решение Докажем, что этот предел равен 3. Действительно, для всех  выполняются неравенства
выполняются неравенства
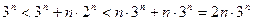 .
.
Тогда, извлекая корни степени п из всех частей неравенства, получим
|
|
|
 .
.
Так как 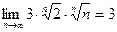 , то
, то  .
.
Пример 7  .
.
Решение Заметим, что для любого натурального 
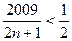 .
.
Тогда  имеем
имеем
 .
.
Так как  , то
, то  .
.
Задание 8
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Пример 1 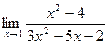 .
.
Решение Перейдем к пределу в числителе и знаменателе. Получим  .
.
Пример 2  .
.
Решение При 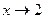 и числитель, и знаменатель дроби стремятся к нулю. Т. е. имеем неопределенность вида
и числитель, и знаменатель дроби стремятся к нулю. Т. е. имеем неопределенность вида  . Разложим числитель и знаменатель на множители. Корнями знаменателя являются
. Разложим числитель и знаменатель на множители. Корнями знаменателя являются  и
и  . Поэтому
. Поэтому  .
.
Пример 3 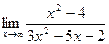 .
.
Решение Имеем неопределенность вида  . Чтобы от нее избавиться, разделим числитель и знаменатель дроби на х в старшей степени, т. е. на
. Чтобы от нее избавиться, разделим числитель и знаменатель дроби на х в старшей степени, т. е. на  . Получим
. Получим
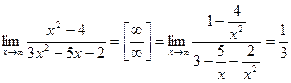 .
.
Пример 4 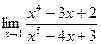 .
.
Решение Имеем неопределенность вида  . Разложим числитель и знаменатель на множители.
. Разложим числитель и знаменатель на множители.

 .
.
Пример 5  .
.
Решение Имеем неопределенность вида  . Умножим числитель и знаменатель дроби на выражения, сопряженные к числителю и знаменателю, т. е. на
. Умножим числитель и знаменатель дроби на выражения, сопряженные к числителю и знаменателю, т. е. на  . Получим
. Получим

 .
.
Пример 6 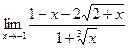 .
.
Решение Имеем неопределенность вида  . Умножим числитель и знаменатель дроби на выражения, сопряженные к числителю и знаменателю, т. е. на
. Умножим числитель и знаменатель дроби на выражения, сопряженные к числителю и знаменателю, т. е. на  .
.
Получим 


Пример 7 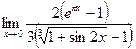 .
.
Решение Имеем неопределенность вида  . Воспользуемся эквивалентностью функций при
. Воспользуемся эквивалентностью функций при  (Приложение А м. зуемся эквивалентностью функций при).
(Приложение А м. зуемся эквивалентностью функций при).
Так как при 
 и
и  , то при
, то при  имеем
имеем
 ,
,  .
.
Тогда  .
.
Пример 8  .
.
Решение Имеем неопределенность вида  . Перейдем к новой переменной
. Перейдем к новой переменной 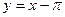 . Так как
. Так как  , то
, то  . Получим
. Получим
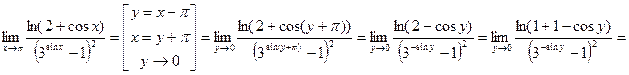
 .
.
При 
 ,
,
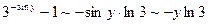 .
.
Поэтому последний предел равен  .
.
Задание 9
Найдите односторонние пределы функции
 в точке
в точке 
или докажите, что соответствующий односторонний предел не существует.
Решение Правосторонний предел функции 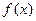 в точке
в точке  существует. Действительно,
существует. Действительно,
 .
.
Покажем, что предела слева функции 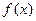 в точке
в точке  не существует. В соответствии с определением по Гейне предела функции в точке, достаточно указать две последовательности
не существует. В соответствии с определением по Гейне предела функции в точке, достаточно указать две последовательности  , сходящиеся к нулю слева, такие, что соответствующие значения функции
, сходящиеся к нулю слева, такие, что соответствующие значения функции 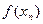 будут иметь различные пределы при
будут иметь различные пределы при  .
.
Возьмем  ,
, 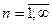 .
.
 ,
,  при
при  .
.
Возьмем теперь 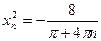 ,
, 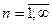 .
.
 ,
, 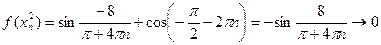 при
при 
Согласно определению по Гейне предела функции в точке,  не существует.
не существует.
Задание 10
Используя I и II замечательные пределы, вычислить пределы функций.
Пример 1  .
.
Решение Имеем неопределенность вида  . Воспользуемся первым замечательным пределом и теоремой о произведении пределов. Получим
. Воспользуемся первым замечательным пределом и теоремой о произведении пределов. Получим
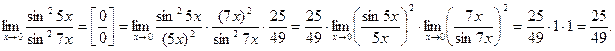
Пример 2  .
.
Решение 
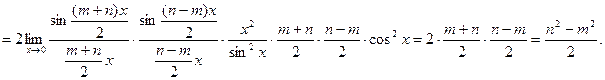
Пример 3  .
.
Решение 

Пример 4  .
.
Решение Имеем неопределенность вида  . Введем новую переменную
. Введем новую переменную  , тогда
, тогда  и
и

 .
.
Пример 5  .
.
Решение Имеем неопределенность вида [  ]. Воспользуемся вторым замечательным пределом.
]. Воспользуемся вторым замечательным пределом.

 .
.
Пример 6  .
.
Решение Имеем неопределенность вида [  ]. Воспользуемся вторым замечательным пределом.
]. Воспользуемся вторым замечательным пределом.
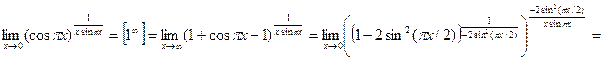
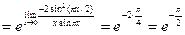 , так как
, так как
 .
.
Примечание Использование известных асимптотических равенств несколько упрощает решение задач. Например,
 .
.
Пример 7  .
.
Решение Имеем неопределенность вида [  ]. Воспользуемся вторым замечательным пределом.
]. Воспользуемся вторым замечательным пределом.

 , так как
, так как
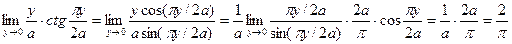 .
.
Задание 11
Исследовать данные функции на непрерывность, найти точки разрыва и определить их тип.
Пример 1  .
.
Решение Так как  , то данную функцию можно записать следующим образом:
, то данную функцию можно записать следующим образом:
 .
.
Данная функция не определена в точках  и
и  , значит, эти точки являются точками разрыва. Определим их тип.
, значит, эти точки являются точками разрыва. Определим их тип.
Найдем односторонние пределы:
 ,
,  .
.
Так как в точке  существуют односторонние пределы, но они различны, то
существуют односторонние пределы, но они различны, то  – точка разрыва I рода.
– точка разрыва I рода.
Так как  , то
, то  – точка разрыва II рода.
– точка разрыва II рода.
Исследуем теперь функцию на непрерывность в точке  .
.
 ,
, 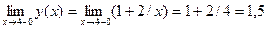 .
.
Поскольку в точке  односторонние пределы существуют и равны, то существует
односторонние пределы существуют и равны, то существует 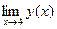 и равен 1,5. А так как предел функции
и равен 1,5. А так как предел функции  в точке
в точке  совпадает со значением функции в этой точке, то данная функция непрерывна в точке
совпадает со значением функции в этой точке, то данная функция непрерывна в точке  .
.
Если  , то данная функция непрерывна по определению непрерывной функции (в каждой такой точке предел функции совпадает со значением функции в этой точке).
, то данная функция непрерывна по определению непрерывной функции (в каждой такой точке предел функции совпадает со значением функции в этой точке).
Построим схематически график функции  (рисунок 1).
(рисунок 1).

Рисунок 1 − График функции  .
.
Пример 2  .
.
Решение Найдем точки, в которых знаменатель обращается в ноль. Решив уравнение  , получим
, получим  ,
,  .
.
Так как функция не определена в этих точках, то  и
и  – точки разрыва. Определим их тип. Вычислим пределы функции в этих точках.
– точки разрыва. Определим их тип. Вычислим пределы функции в этих точках.

Так как существует конечный предел функции в точке  , то
, то  – точка устранимого разрыва.
– точка устранимого разрыва.
Так как  , то
, то  – точка разрыва II рода.
– точка разрыва II рода.
В остальных точках данная функция непрерывна как отношение непрерывных функций.
Пример 3 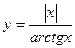 .
.
Решение Данная функция не определена в точке  , значит, она разрывна в этой точке. Рассмотрим ее односторонние пределы в этой точке.
, значит, она разрывна в этой точке. Рассмотрим ее односторонние пределы в этой точке.
 ,
,
 .
.
Односторонние пределы существуют, но различны. Значит,  – точка разрыва I рода.
– точка разрыва I рода.
Поскольку при 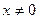 знаменатель
знаменатель  не обращается в ноль, то в остальных точках данная функция непрерывна как отношение непрерывных функций.
не обращается в ноль, то в остальных точках данная функция непрерывна как отношение непрерывных функций.
Пример 4  .
.
Решение Данная функция принимает всего три значения: 0, 1 и –1 – в зависимости от знака выражения  . Поэтому запишем ее в следующем виде:
. Поэтому запишем ее в следующем виде:
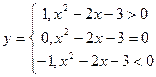 , т. е.
, т. е.  .
.
Рассмотрим, например точку  (рисунок 2).
(рисунок 2).
 ,
, 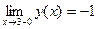 .
.

Рисунок 2 − График функции  .
.
Значит,  – точка разрыва I рода.
– точка разрыва I рода.
Аналогично доказывается, что 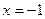 – тоже точка разрыва I рода.
– тоже точка разрыва I рода.
В остальных точках функция является кусочно-постоянной, а значит, непрерывна.
Задание 12
Установить, верно ли утверждение:
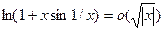 при
при  .
.
Решение Воспользуемся леммой:
если  в некоторой проколотой окрестности точки
в некоторой проколотой окрестности точки  , то
, то
 при
при 

 .
.
Функция  для любого
для любого 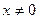 . Вычислим
. Вычислим 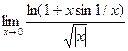 .
.
Заметим, что величина  является бесконечно малой при
является бесконечно малой при  как произведение бесконечно малой функции
как произведение бесконечно малой функции  и ограниченной
и ограниченной  . Поэтому при
. Поэтому при  выполняется
выполняется  .
.
Тогда  ,
,
так как  при
при  , а
, а  .
.
В силу леммы, данное утверждение верно.
Задание 13
Найти  , вычислив
, вычислив  .
.
Пример 1  .
.
Решение Преобразуем  .
.
Пусть


