Струйная модель движущейся ж.

При изучении поступ-го движ-я использ-ся струйная модель ж. Элем-ми этой модели явл-ся линии тока, трубки тока и элементарные струйки. Линии тока – это линия, в каждой точке к-ой в данный момент времени вектор скорости ж совпадает с касательной этой линии. Рис. Трубка тока – это поверхность, образованная линиями тока нормальными в каждой точке бесконечно малого замкнутого контура. Рис. Элементарная струйка – это ж, движущаяся внутри трубки тока. Элементарную струйку можно представить в виде движ-ся жидких частиц плотно нанизанных на линию тока (подобно бусинкам на нитке). Элементар-я струйка обладает след-ми св-ми: 1. Ж не входит и не выходит через боковую поверх-ть элементарн-й струйки. Элементар-я струйка не пронизана. 2. Скорость и др параметры ж в пределах поперечного сеч-я измен-ся на беск малую величину. Это объясняется малыми размерами поперечн сеч-я элементар-ой струйки. Вдоль элемен-ой струйки скорость может измен-ся от сечения к сечению. Часто рассматрив-т среднюю по сечению скорость, к-ю принимают постоянной величиной.

Потоки ж.

Потоком наз-ют движущуюся массу ж, ограниченную направляющими поверхностями. По харак-ру и сочетанию ограниченных поверхностей различают безнапорные, напорные потоки и гидравлические струи. 1. Безнапорный поток. Примером может служить поток ж в канале или трубе, работающей в неполном сеч-ии. Безнапорный поток – поток, ограниченный частично твердой и частично свободной поверхностями. Рис. 2. Напорный поток – это поток, ограниченный твердыми направляющими поверх-ми. N: поток ж в трубе, работающей полным сечением. Рис. 3. Гидравлическая струя – это поток, ограниченный только ж или толко газовой средой. N: струя из пожарного трансполта. Рис. Струя, огранич-я газовой средой наз-ся свободной. Струя, огранич-й ж наз-ся затопленной. В рамках струйной модели ж поток рассмат-ся как бесконечная совокупность элементар-х струек, к-е не перемещ-ся, а при разных скоростях скользят относ-но друг друга.

Живое сечение потока. Расход. Средняя скорость.

Живое сечение потока или просто сеч-е потока – это поверхность в пределах потока нормальная в каждой своей точке, к проходящим через них линиям тока. Рис. Живое сечение – сложная поверх-ть. При равномерном движ-ии ж, живое сеч-е явл-ся плоским, основной хар-ой живого сечения явл-ся его площадь. Есть и др характер-ки.

Расход – это кол-во ж, проходящей через живое сечение потока в единицу времени. Кол-во ж может измер-ся в ед-ах объема массы и веса. Поэтому различают объемный, массовый и весовой расходы. Q- объемный расход (м³/с), Q_m-массовый расход (кг/с), Q_G –весовой расход (Н/с), Q_m=ρQ, Q_G=gQ_m=gρQ.В дальнейшем будем использовать объемный расход. Рис.Определим расход потока. Пусть за время dt ж, находившаяся в сеч-ии 1-1 переместилась в сеч-е 2-2, отстоящее от начального на расстояние dl. Объем ж, к-й прошел через сечение 1-1 равен: dV=dSdl, dQ=dV/dt=dldS/dt=VdS, где V=dl/dt – скорость ж в сеч-ии 1-1. Q= 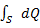= 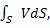м³/с. Расход – это основной параметр потока.

Средняя скорость в данном сечении потока определ-ся как частное от деления объемного расхода на площадь живого сечения. V_ср=Q/S, средняя скорость по сечению – это скорость, при которой расход через данное сечение = действительному расходу. V_срS=Q. В левой части ур-я- расход, опред-й по средней скорости, в правой-действит-й расход. Q=V_срS.

Уравнение неразрывности.

В соответствии со струйной моделью ж поток можно представить бесконечной совокупностью этих струек. Элемен-е струйки явл-ся непроницаемыми, а жид-ть сплошной и несжимаемой, поятому объемный расход вдоль потока есть вел-на постоянная: Q=const вдоль потока, V_срS=const вдольпотока (1).

Соотношение (1) наз-ся уравнением неразрывности или урав-ем постоянства расхода вдоль потока. Оно явл-ся математ-им выражением принципа сплошности и з-на сохранения массы. Из последнего соотношения следует, что с увеличением площадки живого сечения средняя скорость в нем уменьш-ся и наоборот с уменьшением площади сечения скорость увелич-ся. Рис с примером. Скорсти в сеч-ях обратно пропорциональны их площадям.