Задача об оптимальном использовании ресурсов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ № 6

по дисциплине

ИНФОРМАТИКА

 

Разработчик: к.т.н., доц. Баранова Е.М.

 

 

Тула, 2018 г.

Лабораторная работа № 6

Решение задач широкого спектра средствами электронных таблиц

(MS EXCEL, ООо Calc)

6.1. Цель работы

Изучение инструментов электронных таблиц, предназначенных для решения задач широкого спектра.

6.2. Теоретические положения

Основной возможностью электронных таблиц является процесс математического моделирования в любой предметной области. Математическое моделирование – это описание на языке формул основных зависимостей, подлежащих изучению и исследованию в проблемной области. Электронные таблицы содержат широкий спектр функций различного прикладного аспекта, и позволяют пользователю самостоятельно создавать зависимости путем ввода в ячейки таблиц переменных, значений, констант и прочее. Любая вводимая пользователем в ячейки электронной таблицы зависимость должна начинаться со знака равно (рисунок 1):

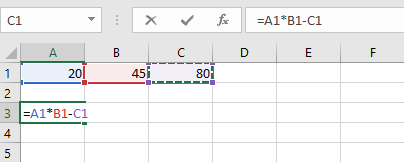
Рисунок 1 – Фрагмент электронной таблицы с вводимой формулой

Достаточно часто в качестве экономических инструментов электронных таблиц могут выступать инструменты математического программирования.

Математическое программирование – это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.

Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскание оптимума (максимума или минимума) заданной линейной функции при наличии ограничений в виде линейных уравнений или линейных неравенств.

Для решения задач экономики математическими методами выражают экономическое содержание задачи через определенные математические зависимости, т.е. составляют так называемую экономико-математическую модель задачи.

Задача об оптимальном использовании ресурсов

Постановка задачи. Предположим, что предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (разных видов сырья, вспомогательных материалов, запасов машинного времени, людских ресурсов и т.д.) Эти ресурсы ограничены и составляют в планируемый период соответственно b₁, b₂,..., b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы j-го вида изделия (i=1, 2,..., m; j=1, 2,..., n). Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна с_j (j=1, 2,..., n). В планируемый период все показатели a_ij, c_j, и b_i предполагаются постоянными.

Требуется составить такой план выпуска продукции, при котором прибыль предприятия от реализации ее была бы наибольшей.

Математическая формулировка задачи выглядит следующим образом.

Требуется найти такие неотрицательные значения x₁, x₂,... x_n (x_j - количество единиц изделия j- го вида), которые удовлетворяли бы системе ограничений:

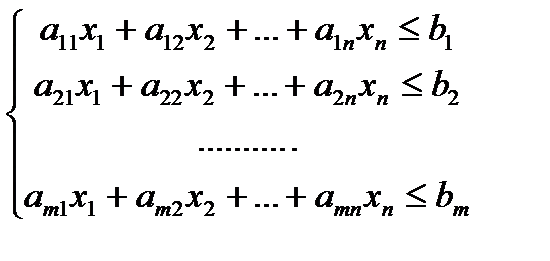причем ,

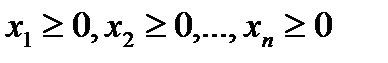и при которых прибыль от реализации всей продукции F=c₁x₁+c₂x₂+...+c_nx_n была бы максимальной. Функция F выражает конечную цель оптимального планирования, в данном случае - получение наибольшей прибыли, поэтому эту функцию называют целевой.

Пример 1. Компания производит телевизоры, стерео и акустические системы. Прибыль от производства одного телевизора - 75 условных единиц (у.е.), стереосистемы - 50 у.е., акустической системы - 35 у.е. На складе имеется 450 шт. шасси, 250 кинескопов, 800 громкоговорителей, 450 источников питания, 600 радиодеталей. Для производства одной единицы продукции требуется некоторое количество деталей (таблица 1).

Таблица 1 – Перечень и количество деталей для производства одной единицы продукции

Название детали	Телевизор	Стерео система	Акустическая система
Шасси	1	1	0
Кинескоп	1	0	0
Громкоговоритель	2	2	1
Источник питания	1	1	0
Радиодетали	2	1	1

 

Определить план выпуска продукции при котором прибыль предприятия будет максимальна.

Экономико-математическая модель задачи выглядит так:

F=75x₁+50x₂+35x_n  -> max

при ограничениях

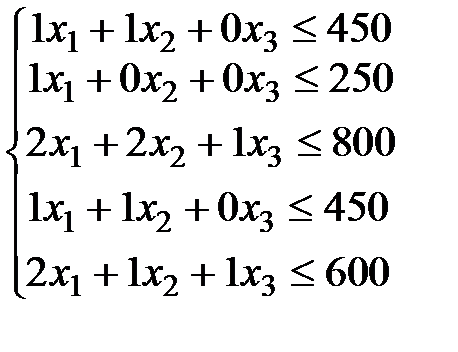 причем ,

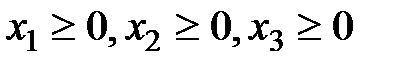Для решения задачи с помощью электронной таблицы Excel введем на рабочий лист входные данные (рисунок 2).

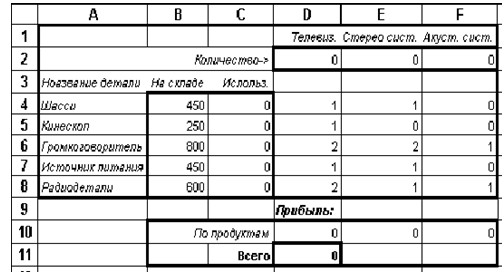
Рисунок 2 – Входные данные задачи

об оптимальном использовании ресурсов

Причем в некоторых ячейках содержатся формулы, представленные в таблице 2:

Таблица 2 – Перечень формул в ячейках электронной таблицы (для задачи об оптимальном использовании ресурсов)

Ячейка	Формула
D10	75*D2
E10	50*E2
F10	35*F2
D11	D10+E10+F10
С4	D$2*D4+E$2*E4+F$2*F4
С5	D$2*D5+E$2*E5+F$2*F5
C6	D$2*D6+E$2*E6+F$2*F6
C7	D$2*D7+E$2*E7+F$2*F7
C8	D$2*D8+E$2*E8+F$2*F8

Решение задачи производится с помощью пункта меню Сервис/ Поиск решения. При этом в диалоговом окне вводятся следующие значения:

1. Целевая ячейка - D11.

2. Максимальное значение.

3. Изменяя ячейки D2:F2.

4. Добавить ограничения:

ссылка на ячейки C4:C8

ограничение <=B4:B8

5. Добавить ограничения

ссылка на ячейки D2:F2

ограничение >=0

6. Выполнить.

После поиска решения необходимо сохранить найденное решение, которое будет иметь вид: количество телевизоров - 200, стереосистем - 200, аудиосистем - 0; полученная прибыль 25000 условных единиц.

Задача о смесях

К группе задач о смесях относятся задачи по отысканию наиболее дешевого набора из отпущенных исходных материалов, обеспечивающего получение смеси с заданными свойствами.

Постановка задачи. Имеется m видов материалов. Стоимость единицы материала i-го вида с_i. Каждый вид материалов состоит из не более чем n компонент. Количество j -го компонента в единице i-го материала соответственно a_ij. Необходимо составить смесь, имеющую заданные свойства, т.е. количество j-го компонента в смеси не менее b_j. Затраты на приобретение материалов для смеси должны быть минимальны.

Математическая формулировка задачи выглядит следующим образом.

Требуется найти такие неотрицательные значения x₁, x₂,... x_m (x_i - количество материала i- го вида в смеси), которые удовлетворяли бы системе ограничений

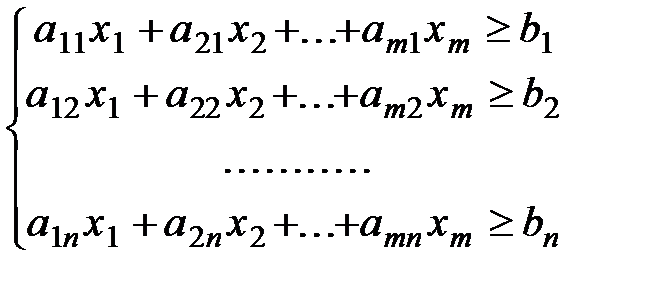 причем ,

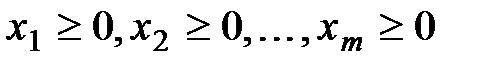и при которых стоимость смеси F=c₁x₁+c₂x₂+...+c_mx_m была бы минимальной.

 Пример 2. На свиноферме производится откорм свиней. Известно, что каждая свинья должна ежедневно получать не менее 6 единиц жиров, 8 ед. белков, 12 ед. углеводов. Для откорма свиней можно закупить три вида кормов: картофель, жмых и комбикорм. Содержание каждого вещества в различных видах корма и стоимость единицы каждого корма приведены в таблице 3.

Таблица 3 – Содержание каждого вещества в различных видах корма и стоимость единицы каждого корма

Вид	Вещества			Стоимость
корма	жиры	белки	углеводы	единицы корма
жмых	2	1	3	2
комбикорм	1	2	4	3
картофель	3	1.5	2	2.5

 

Требуется обеспечить наиболее дешевый рацион откорма.

Экономико-математическая модель задачи:

F=2x₁+3x₂+2.5x₃  -> min

при ограничениях

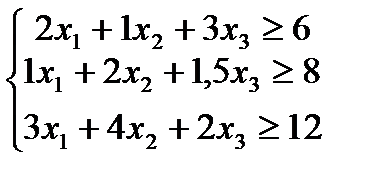причем ,

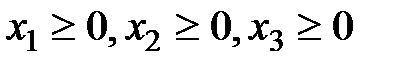Для решения задачи введем на рабочий лист Excel следующий данные (рисунок 3).

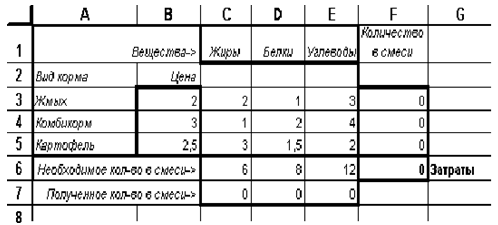
Рисунок 3 – Входные данные задачи о смесях

Причем в некоторых ячейках содержатся формулы (таблица 4).

Таблица 4 – Перечень формул в ячейках электронной таблицы (для задачи о смесях)

Ячейка	Формула
F6	=СУММПРОИЗВ(B3:B5;F3:F5)
C7	=СУММПРОИЗВ(C3:C5;$F$3:$F$5)
D7	=СУММПРОИЗВ(D 3: D 5;$F$3:$F$5)
E7	=СУММПРОИЗВ(E 3:E5;$F$3:$F$5)

 

Решение задачи производится с помощью пункта меню Сервис/ Поиск решения. При этом в диалоговом окне вводятся следующие значения:

1. Целевая ячейка - F6.

2. Минимальное значение.

3. Изменяя ячейки F3:F5.

4. Добавить ограничения:

ссылка на ячейки C7:E7

ограничение >=C6:E6

5. Добавить ограничения

ссылка на ячейки F3:F5

ограничение >=0

6. Выполнить.

После поиска решения необходимо сохранить найденное решение, которое будет иметь вид: жмых использовать не стоит, картофель - 0,88 единицы, комбикорм - 3,33 ед.; при этом затраты на одну свинью составят 12,22 условных единиц в сутки.

Транспортная задача

Простейшими транспортными задачами являются задачи о перевозках некоторого однородного груза из пунктов отправления (от поставщиков) в пункты потребления (к потребителям) при обеспечении минимальных затрат на перевозки.

Постановка задачи. На k предприятиях производится некоторый продукт, причем мощность i-го поставщика в планируемый период (т.е. количество производимого продукта) M_i. Продукт необходимо поставить l потребителям, причем мощность j-го потребителя в планируемый период (требуемое количество продукта) N_j. Показатель a_ij отражает затраты на перевозку единицы груза от i-го поставщика к j-му потребителю. Необходимо найти такое распределение потребителей и поставщиков при котором общие затраты на перевозки были бы минимальны.

Различают закрытую и открытую модели. Модель называется закрытой если 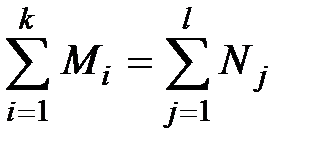, в противном случае модель - открытая.

Математическая формулировка задачи для закрытой модели выглядит следующим образом.

Требуется найти такие неотрицательные значения x₁₁, x₁₂,... x_kl (x_ij - количество единиц продукта поставляемого от i- го поставщика к j -му потребителю), которые удовлетворяли бы системе ограничений

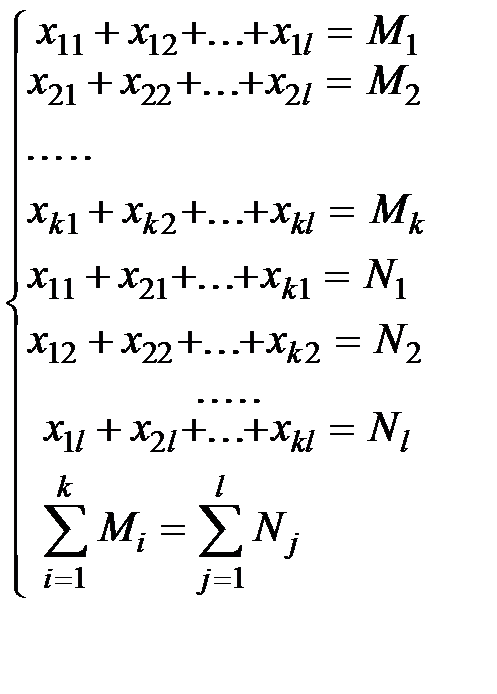причем 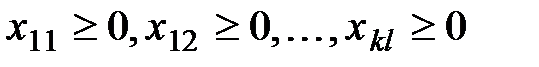, (1)

и при которых затраты на перевозку груза F=a₁₁ x₁₁ + a₁₂ x₁₂ +...+a_ijx_ij  +... + a_klx_kl были бы минимальны.

Пример 3. На четырех складах фирмы хранится сахар в мешках, причем на первом складе - 100 мешков, на втором - 125, на третьем - 75, на четвертом - 75. Фирма заключила договор на поставку пяти организациям: ООО Марс - 85 мешков, АО Рита - 65, ЗАО Град - 80, ТОО Форд - 75, ЧП Шпак - 70 мешков.

 

Затраты на перевозку из одного пункта в другой приведены в таблице 5.

Таблица 5 – Затраты на перевозку из одного пункта в другой

Склад	ООО Марс	АО Рита	ЗАО Град	ТОО Форд	ЧП Шпак
Склад 1	4	2	3	1	2
Склад 2	6	5	3	4	3
Склад 3	1	2	5	6	5
Склад 4	6	4	5	2	3

 

Определить план доставки груза потребителям при котором затраты на перевозку будут минимальны.

Экономико-математическая модель задачи

F=4x₁₁+2x₁₂+3x₁₃+1x₁₄+2x₁₅+6x₂₁+5x₂₂+3x₂₃+4x₂₄+3x₂₅+1x₃₁+2x₃₂+5x₃₃+6x₃₄+

+5x₃₅+6x₄₁+4x₄₂+5x₄₃+2x₄₄+3x₄₅ ->min

при ограничениях

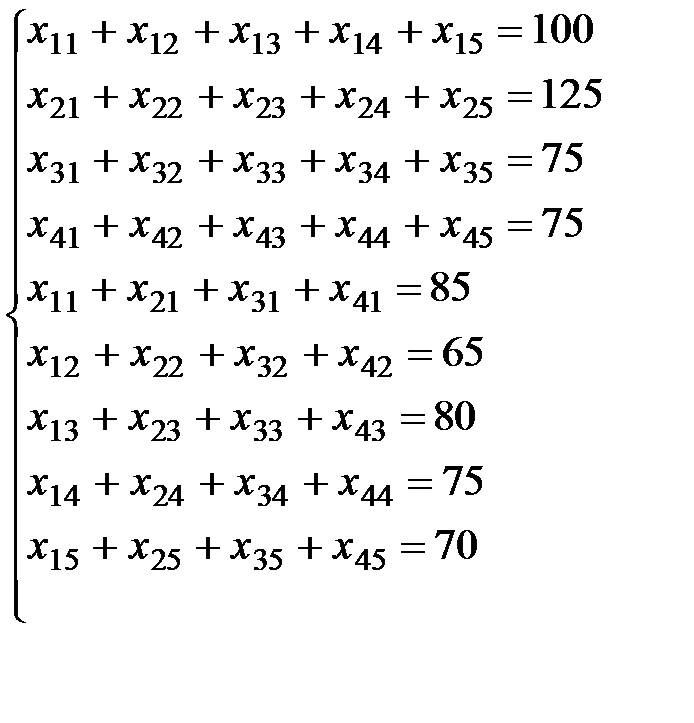причем ,

Для решения задачи введем на рабочий лист Excel следующий данные (рисунок 5).

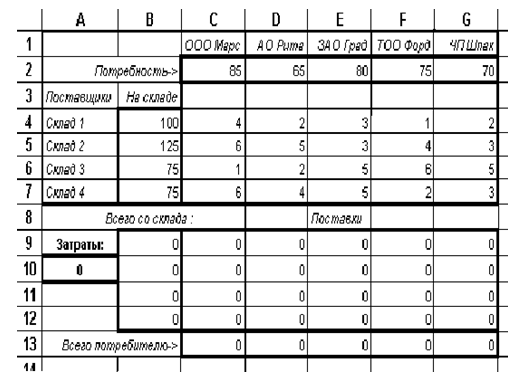
Рисунок 5 – Входные данные транспортной задачи

Причем в некоторых ячейках содержатся формулы (таблица 6).

Таблица 6 – Перечень формул в ячейках электронной таблицы (для транспортной задачи)

Ячейка	Формула
B9	=СУММ(C9:G9)
B10	=СУММ(C 10:G 10)
B11	=СУММ(C 11:G 11)
B12	=СУММ(C 12:G 12)
A10	=СУММПРОИЗВ(C4:G7;C9:G12)
C13	=СУММ(C9:C12)
D13	=СУММ(D 9: D 12)
E13	=СУММ(E 9: E 12)
F13	=СУММ(F 9: F 12)
G13	=СУММ(G 9: G 12)

 

Решение задачи производится с помощью пункта меню Сервис/ Поиск решения. При этом в диалоговом окне вводятся следующие значения:

1. Целевая ячейка - A10.

2. Минимальное значение.

3. Изменяя ячейки C9:G12.

4. Добавить ограничения:

ссылка на ячейки B9:B12

ограничение =B4:B7

5. Добавить ограничения:

ссылка на ячейки C13:G13

ограничение =C2:G2

6. Добавить ограничения

ссылка на ячейки C9:G12

ограничение >=0

7. Выполнить.

После поиска решения необходимо сохранить найденное решение, которое будет иметь вид: ООО Марс необходимо доставить 10 мешков со склада 1 и 75 мешков со склада 4; АО Рита - 65 мешков со склада 1; ЗАО Град - 80 со склада 2; ТОО Форд - 25 с первого склада и 50 с второго; ЧП Шпак - 45 со склада 2 и 25 со склада 4. При этом затраты на доставку составят 820 условных единиц.

6.3. Задание на работу

Основное

Решить задачу при помощи модуля «Поиск решения» («Решатель»):

Фермер закупает удобрения двух видов. В единице массы удобрения первого вида содержится:

- 3 условные единицы химического вещества а;

- 2 условные единицы химического вещества b;

- 1 условная единица химического вещества с.

В единице массы удобрения второго вида содержится:

- 1 условная единица химического вещества а;

- 1 условная единица химического вещества b;

- 1 условная единица химического вещества с.

 На 1 га почвы необходимо внести:

- 9 условных единиц химического вещества а;

- 8 условных единиц химического вещества b;

- 6 условных единиц химического вещества с.

 Составить наиболее экономичный план закупки удобрений (в расчете на 1 га), если цены удобрений (на 1 ед. массы) таковы:

- 1 вид – 3 денежные единицы;

- 2 вид – 2 денежные единицы.

Дополнительное

Решить задачу путем математического моделирования (ввода формул в ячейки электронной таблицы).

Вариант 1

Известен ежедневный доход индивидуального предпринимателя в течение месяца (двадцать четыре рабочих дня) d ₁, d ₂, d ₃, d ₄ … d ₂₄ рублей в день. Рассчитать месячный доход индивидуального предпринимателя D:

.

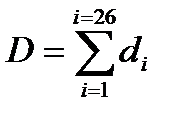D<15 000 000, так как только в этом случае индивидуальный предприниматель имеет право платить налоги по упрощенной системе налогообложения.

Рассчитать сумму S, с которой будет заплачен налог:

, где

БД – базовая доходность. В упрощенной системе налогообложения принимается равной 1 800 рублей;

F – арендуемая индивидуальным предпринимателем площадь помещения;

К₁ =1,096 – корректирующий коэффициент;

К₂ =1, К₃ =0,7, К₄ =0,97 – поправочные коэффициенты.

Рассчитать сумму единого вмененного налога N:

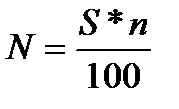, где

S – сумма, с которой будет заплачен налог;

n – процент налогообложения. В упрощенной системе налогообложения принимается равным 15%.

Каждый месяц d ₁, d ₂, d ₃, d ₄ … d ₂₄ и F  могут изменяться.

Периодически БД, К_1,   К₂, К₃, К_4,    n также могут изменяться.

Вариант 2

Фирма берет в кредит 5 автомобилей. Стоимость каждого автомобиля Х тысяч рублей. Фирма располагает начальной суммой Y тысяч рублей.

Банк предлагает 3 условия кредитования:

- Авто-кредит. Процентная ставка – 13% годовых. Ежемесячное кассовое обслуживание 0,5% от суммы кредита. Первоначальный взнос необязателен. Обязательное страхование АВТОКАСКО – 15% от стоимости автомобиля. Сумму страхования по АВТОКАСКО можно включить в кредит. Возможно досрочное погашение кредита с перерасчетом процентов.

- Кредит на неотложные нужды. Процентная ставка – 19% годовых. Ежемесячное кассовое обслуживание 1,2 % от суммы кредита. Первоначальный взнос обязателен – 10% от суммы кредита. Через шесть месяцев возможно досрочное погашение кредита с перерасчетом процентов.

- Потребительский кредит. Процентная ставка – 15% годовых. Ежемесячное кассовое обслуживание 0,8 % от суммы кредита. Первоначальный взнос обязателен – 12 % от суммы кредита. Возможно досрочное погашение кредита, однако в этом случае плательщик обязан внести 2% от суммы кредита.  

Кредиты можно взять на 12, 24, 36, 48, 60 месяцев.

Определить наиболее выгодные условия кредита.

 

Вариант 3

Предприятие платит налоги по полной системе налогообложения. Ежемесячный доход предприятия меньше 15 000 000, поэтому налог на добавленную стоимость (НДС) платится раз в квартал. Известна сумма дохода предприятия в квартал S _кв. Рассчитать начисленную сумму НДС, которая равна 18% от суммы дохода предприятия в квартал S _кв. В этот же квартал предприятию выставлены счета за отопление и воду.

Счет за отопление в квартал равен X рублей, в том числе НДС 18%.

Счет за воду в квартал равен Y рублей, в том числе НДС 18%.

Рассчитать сумму НДС к оплате в квартал, которая определяется как разница начисленной суммы НДС и сумм НДС, входящих в оплату счетов за отопление и воду в тот же квартал.

Вариант 4

В фирме работает n сотрудников. Каждый сотрудник имеет оклад X рублей. Девять сотрудников отработали март месяц полностью (двадцать два рабочих дня). Один сотрудник отработал в марте 20 рабочих дней, взяв два дня без оплаты. Рассчитать начисленную заработанную плату каждому сотруднику Z_начисл:

Каждый сотрудник имеет стандартные налоговые вычеты:

- 400 рублей, если нет детей. При этом оклад должен быть меньше 20 000 тысяч рублей, иначе налоговые вычеты отменяются.

- 400+600, если один ребенок;

- 400+1200, если два ребенка. При этом оклад должен быть меньше 40 000 тысяч рублей, иначе налоговые вычеты на детей отменяются.

В фирме двое сотрудников имеют по одному ребенку, у остальных сотрудников детей нет. Процентная ставка налога на доходы физических лиц (НДФЛ) составляет 13%. Рассчитать сумму НДФЛ S_ндфл каждого сотрудника:

.

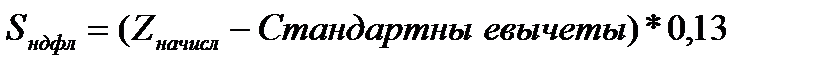Рассчитать сумму НДФЛ S_{ндфл фирм} по фирме:

.

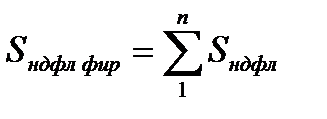Оклад сотрудников, количество сотрудников, имеющих детей, количество рабочих дней, количество фактически отработанных дней могут изменяться.

Поделиться:

Воспользуйтесь поиском по сайту: