Теорема сложения скоростей при сложном движении точки

Определение скоростей точек плоской фигуры. Теорема о проекциях скоростей точек плоской фигуры.

Теорема: Скорость любой точки принадлежащей плоской фигуре равна геометрической сумме скорости полюса и той скорости которую имела бы точка при вращательном движении вокруг оси проходящей через полюс

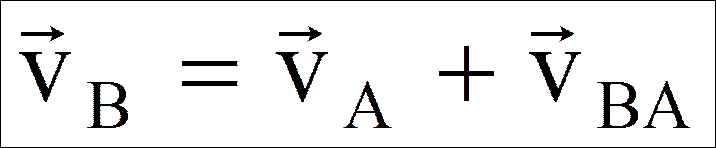
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: v_Acosa = v_Bcosb.

Мгновенный центр скоростей. Определение скорости с помощью МЦС. Частные случаи нахождения МЦС.

МЦС – точка плоскости движения плоской фигуры, скорость которой в данном положении равна 0.

Скорости всех точек будут направлены перпендикулярно отрезкам соединяющим точку и МЦС в сторону угловой скорости и пропорциональны длинам этих отрезков.

Частные случаи определения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. v_A и v_B); 3) если они при этом равны между собой, то м.ц.с. находится в ¥, а угловая скорость w=v_A/¥=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в ¥, и угловая скорость w=v_A/¥=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания

 

 

Определение ускорений точек плоской фигуры. Мгновенный центр ускорений.

Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения точки которое она имела бы при вращательном движении тела вокруг оси проходящей через полюс.

aB=aA+aBA(нормальное)+aBA(тангенциальное)=aA+aBA

aBA(нормальное)=ωAB^2*AB

aBA(тангенциальное)=έAB*AB

Существует 2 способа определения ускорений:

Метод проекций

Построение многоугольника ускорений

20.Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом 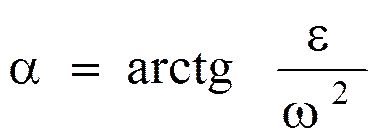к ускорению а_А отрезок 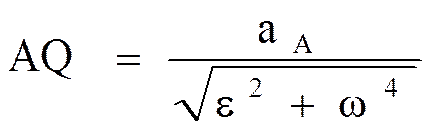, при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол 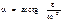: 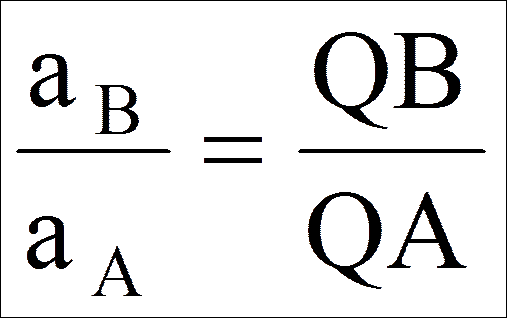. Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.

Сложное движение точки. Абсолютное, относительное и переносное движения. Абсолютные, относительные и переносные скорость и ускорение точки. Основное векторное уравнение кинематики сложного движения.

Сложным называется такое движение тела при котором оно одновременно участвует в двух или нескольких движениях. В рассмотрение вводится подвижная и неподвижная система отсчёта аналогично сложному движению тела. Сложное движение тела рассматривается как совокупность двух движений – относительного и переносного.В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона).

Теорема сложения скоростей при сложном движении точки

Скорость точки относит НСО наз. абсолютной Vабс (Va).Скорость точки относит ПСО наз. относительной Vотс (Vr).Скорость которую имела бы точка находясь в данном положении движущегося тела при отсутствии относит. Движ. Наз. переносная скорость движ. Vпер (Vc). Теор. абсолют скорость точки равна геометр. Сумме относит. и перенос. Скорости Va=Vr+Vc. Док. Пусть точка М приходит в полож М₃ двигаясь по троектории обсолютного движения.(Рис в 4.1).Для определения Vr необход мысленно остановить переносное движ_. Для опред Ve необход мысленно остановить относительное движ. Поэтому для опред. абсолют. Скорости точ. Необход снач. Опред. Полож. Точ. В требуемый момент времени на троектории относит движ.

 

23-24) Теорема сложения ускорений при сложном движении точки. Ускорение Кориолиса. Определение направления ускорения Кориолиса. Правило Жуковского. Смысл ускорения Кориолиса.

1) Переносное движение поступательно. Абсолютное ускорение точки равна геометрич. Сумме относит и переносного движ a_a=a_r+a_e. Если относит движение движ по криволинейной троектории то a_a= a_rⁿ + a_r ^t+a_e.Для определения относит ускорения нужно остановить переносное движение. Для определения переносного ускорения нужно остановить относительное движение.

2)Обсолютное ускорение точки при не поступательном переносном движении равна геометрич сумме a_a=a_r+a_e+ a_с

Кариолисово ускорение характер:1)Изменение велечины переносной скорости в следствии относит движения.2)Изменением направления вектора относит скорости в след непоступательного переносного движ.. a_с =2 a_сώ_e Vrsin(ώ_r,Vr)

Кариолисово ускорение опред по правилу векторного произведения.. a_{с┴ (}ώ_e, Vr) и направлено таким образом чтоб смотря ему навстречу поворот от ώ_e к Vr на найменьший угол происходит против часовой стрелки.

 

Поделиться:

Воспользуйтесь поиском по сайту: