 |
Частные случаи движения точки. Равномерное и равнопеременное движение.
|
|
|
|
Предмет кинематики. Относительность движения. Траектория движения точки. Основная задача кинематики.
Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил.
Основные задачи в кинематике:
1. Определение уравнений движения тела или точки показывающих изменение положения тела в зависимости от времени.
2. По известным уравнениям движения находятся его кинематические характеристики(скорость, ускорение, улов. скорость, и т.д.)
Траектория точки – непрерывная кривая, которую описывает точка при своем движении.
Способы задания движения точки.
Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный.
Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).
Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).
Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).
 Векторный сп. положение точки определяется ее радиус-вектором
Векторный сп. положение точки определяется ее радиус-вектором  , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.
, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.
Скорость точки при векторном способе задания движения.
Вектор скорости: 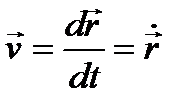 – первая производная от радиус-вектора по времени (точка обозначает производную по времени);
– первая производная от радиус-вектора по времени (точка обозначает производную по времени); 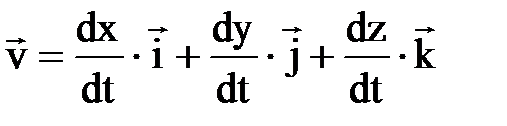 . Проекции скорости:
. Проекции скорости: 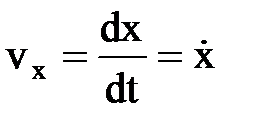 ,
, 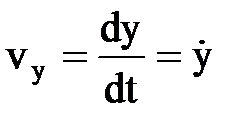 ,
, 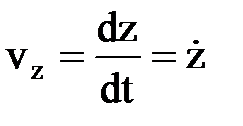 .
.
|
|
|
Модуль скорости:
 ,
,
направляющие косинусы: 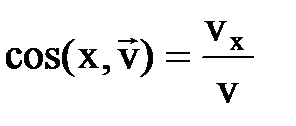 и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
Ускорение точки при векторном способе задания движения.
Ускорение точки. 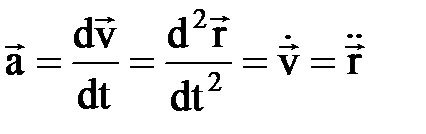 , [м/сек2]. Проекции уск.-я:
, [м/сек2]. Проекции уск.-я: 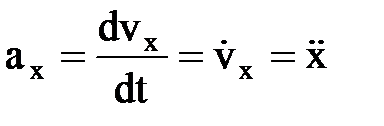 и т.д.
и т.д.
Модуль уск.-я:  ,
,
направляющ. косинусы: 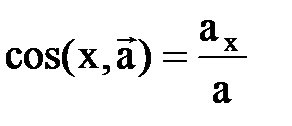 , и т.д.
, и т.д.
При задании движения в полярных координатах: проекции ускорения на радиальное направление 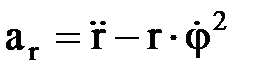 ,
,
 поперечное направление
поперечное направление 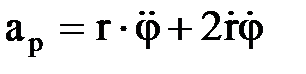 ,
,
модуль ускорения  .
.
Скорость и ускорение точки при координатном способе задания движения.
V= dr/dt = d(xi+yj+zk)/dt = Vxi + Vyj + Vzk где Vx=dx/dt, Vy=dy/dt, Vz=dz/dt – проекции вектора скорости на оси координат V= 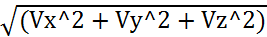
Положени вектора V определяется направлением косинусов, а именно углов между направлением вектора V и положительно направленной соответствующей оси координат.
Скорость точки при естественном способе задания движения.
Скорость точки при естественном способе задания движения равна по модулю первой производной дуговой координаты по времени и направлена по касательной к траектории.

Естественный трехгранник. Разложение ускорения по естественным осям. Касательное и нормальное ускорение.
Если выбрать в качестве осей координат независимые оси ŧ(тау), n, в - которые связаны с движущейся точкой при этом ŧ(тау)-является касательной, n – нормалью, в – бинормалью, тогда ŧ(тау) и n образуют спрямлющую плоскость, n и в нормальную плоскость, в и ŧ(тау) – соприкасающую плоскость, это и есть естественный трёхгранник. Нормальное ускорение точки всегда направлено к центру кривизны траектории 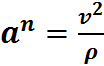 , где
, где 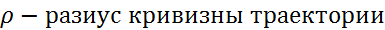 , а касательное по касательной к траектории, если знаки касательного ускорения и скорости совпадают, то и направления их тоже совпадают, или наоборот(
, а касательное по касательной к траектории, если знаки касательного ускорения и скорости совпадают, то и направления их тоже совпадают, или наоборот( )
)
Частные случаи движения точки. Равномерное и равнопеременное движение.
|
|
|
Касательное ускорение показывает изменение скорости по величине, нормально – по направлению.
Равномерное прямолинейное движение:
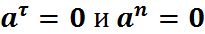
Равномерное криволинейное движение:
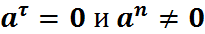
Неравномерное прямолинейное движение:
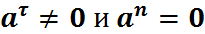
Неравномерное криволинейное движение:
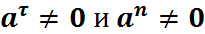
Движение с постоянной скоростью называется прямолинейным.
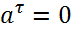

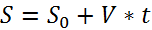
Движение с постоянным ускорением называется равнопеременным.
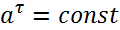


|
|
|


