Тема: Методы детерминированного факторного анализа

Практическое занятие №5

 

Теоретические материалы для решения практических задач:

5.1 Детерминированное моделирование и преобразование
факторных систем

 

Одной из задач факторного анализа является моделирование взаимосвязей между результативными и факторными показателями. Она может быть прямая, детерминированная или косвенная, то есть стохастическая.

В основе детерминированного моделирования факторной системы лежит возможность построения тождественного преобразования для исходной формулы результативного показателя по его теоретически предполагаемым прямым связям с другими факторными показателями.

В детерминированном моделировании факторных систем выделяются следующие их виды:

1. Аддитивные модели, в которых результативный показатель можно представить как алгебраическую сумму факторных показателей:

.

2. Мультипликативные модели, у которых результативный показатель представляет собой произведение факторных показателей:

.

3. Кратные модели, у которых результативный показатель представляет собой частное от деления факторных показателей:

; .

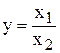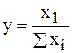4. Комбинированные (смешанные) модели, в которых сочетаются в различных комбинациях предыдущие модели:

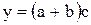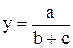; ; и т.д.

Моделирование детерминированных факторных систем осуществляется с помощью следующих основных приемов.

Моделирование аддитивных моделей осуществляется за счет детализации одного или нескольких факторных показателей исходной системы на его составные части.

Исходная факторная система

.

Если представить в виде суммы отдельных слагаемых , то конечная факторная система будет иметь вид: .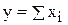

Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы сомножители. В результате получаем ту же факторную систему .

Преобразование кратных моделей осуществляется за счет:

1) удлинения исходной факторной системы путем замены фактора или 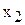на сумму отдельных слагаемых факторов.

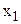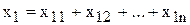При замене на сумму отдельных слагаемых факторов конечная факторная система будет иметь вид : если , то 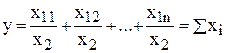. При замене 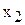на ее составляющие получим модель того же типа, что и исходная факторная система .

2) расширения исходной факторной системы путем умножения числителя и знаменателя дроби на один или несколько новых показателей и создания новой факторной модели вида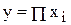

;

3) сокращения исходной факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель.

В результате получается конечная модель того же вида, что и исходная, но с другим набором факторов:

.

 

5.2 Способы измерения влияния факторов в детерминированном анализе

 

Если между факторными и результативным показателем существует строгая функциональная зависимость, то для определения влияния отдельных факторов можно использовать:

1. приемы элиминирования — последовательного выделения влияния одного фактора и исключения влияния остальных факторов: способ цепной подстановки, индексный метод, метод абсолютных и относительных разниц;

2. прием пропорционального деления или долевого участия;

3. интегральный способ;

4. способ логарифмирования.

 

5.2.1. Способ цепной подстановки

 

Используется во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных.

Подстановкой называется замена базисной величины (плановой или фактической за прошлые периоды) каждого факторного показателя в составе результативного на фактическую в отчетном периоде. В результате такой замены рассчитывается один или несколько условных результативных показателей, называемых еще подстановками. Данный условный показатель сравнивается с плановым (базовым) или другим условным результативным показателем. Результат сравнения показывает величину влияния измененного фактора, так как остальные должны быть взяты неизменными.

Следует знать правила применения данного приема.

1. Определяется результативный и факторные показатели.

2. Создается исходная и развитая модель факторной системы. Определяется ее тип.

3. Факторные показатели классифицируются на количественные и качественные, главные и второстепенные.

4. Определяется общее количество используемых для расчета результативных показателей. Оно равно количеству факторов .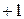

5. Определяется количество условных результативных показателей. Оно равно количеству факторов .

6. При расчете условных результативных показателей в начале заменяются количественные факторы, а потом качественные. Если имеется несколько количественных или качественных факторов, то сначала заменяются главные, а затем второстепенные, зависящие от них.

7.Для правильного определения направления влияния фактора (+,–) надо из результативного показателя, в котором рассчитываемый фактор взят при фактических условиях, вычесть результативный показатель, в котором он взят при плановых условиях.

Рассмотрим алгоритмы и последовательность расчетов для различных типов модели.

Обозначим: результативный показатель – ; факторные показатели: а,b,c; из них: а – главный количественный; b – количественный, зависящий от а; c – качественный.

Исходная мультипликативная модель: .

Поскольку надо рассчитать влияние 3‑х факторов, используются 4 результативных показателя, из них 2 условных.

Плановый результативный показатель

или ;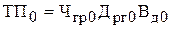

Первый условный результативный показатель (первая подстановка):

или ;

Второй условный результативный показатель (вторая подстановка):

или ;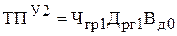

Фактический результативный показатель:

или .

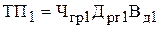Общее (абсолютное) отклонение результативного показателя

или

.

 

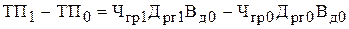Общее (абсолютное) отклонение результативного показателя за счет изменения факторов a, b, c.

или ;

или ;

или .

Алгебраическая сумма влияния факторов должна быть равна общему приросту результативного показателя или . Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.

Кратные модели: ;

; ;

; ;

; ;

.

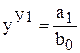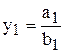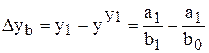Cмешанные модели: ; ;

;	;
;	;
;	;
;	;
\ ;	;
;	;
;   ;	; .

 

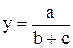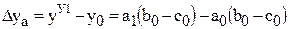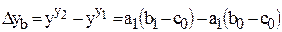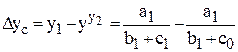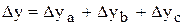Аналогичным образом рассчитывают влияние факторов и по другим моделям смешанного типа.

 

5.2.2. Индексный метод

 

Основан на относительных показателях динамики, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в плановом (базисном) периоде.

Используется для определения влияния факторов на результативный показатель только в мультипликативных моделях.

Исходная модель .

Общий индекс результативного показателя:

.

Относительное изменение результативного показателя за счет факторов

a, b, c:

; ; .

Абсолютное изменение результативного показателя за счет факторов a, b, c:

;

;

.

 

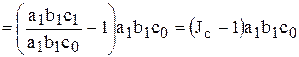5.2.3. Способ абсолютных разниц

 

Применяется в мультипликативных моделях и смешанных моделях типа .

При его использовании величина влияния факторов на изменение результативного показателя рассчитывается умножением абсолютного прироста исследуемого фактора на плановую (базовую) величину факторов, которые находятся в модели справа от него, и на фактическую величину факторов, расположенных слева от него.

Рассмотрим алгоритмы расчета:

для мультипликативной факторной модели типа:

; ;

; ;

;

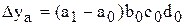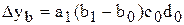для смешанной модели типа .

; ; ; .

 

 

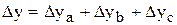5.2.4. Способ относительных разниц

 

Применяется в мультипликативных моделях. Есть несколько вариантов расчета влияния факторов на изменение результативного показателя.

Первый способ: используются относительные отклонения факторных показателей, выраженные в процентах.

Исходная модель:

; ; ;

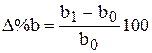Тогда ; ;

; .

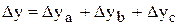Второй и третий способы: используются коэффициенты и индексы изменения факторных показателей.

; ;

.

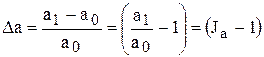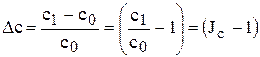Тогда ;

;

;

.

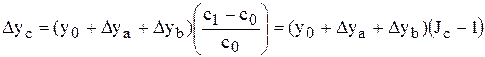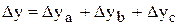Для третьего способа можно использовать еще и такой метод расчета влияния факторов на результативный показатель

; ; .

Способ четыре: прием процентных разностей.

Исходная модель

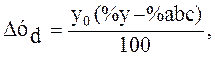
где ; ; ; 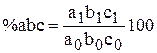- процент выполнения плана соответственно по факторам “a”, “ ”, “ ” и по результативному показателю.

 

5.2.5. Способ пропорционального деления или долевого участия

 

Сущность способа пропорционального деления состоит в пропорциональном делении прироста результативного показателя по факторам его обусловившим, а долевого участия — в определении доли участия каждого фактора в общем приросте результативного показателя.

Эти способы применяются для аддитивных, мультипликативных, кратных и смешанных моделей типа .

Для определения влияния отдельных факторов на прирост результативного показателя рассчитывается один из следующих коэффициентов:

1) коэффициент пропорционального деления , как отношение общего относительного прироста результативного показателя к сумме относительных изменений факторных показателей.

При аддитивных типах моделей рассчитывается один коэффициент пропорциональности, а при других типах моделей — он определяется для каждого порядка факторов в отдельности.

При исходной модели ,

(изменения всех составляющих взяты в относительных единицах).

;

; ;

.

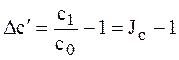2) коэффициент долевого участия , который определяется как отношение относительного прироста i‑го факторного показателя к сумме относительных изменений факторных показателей.

Например, для исходной факторной модели , коэффициент долевого участия для фактора «а»:

.

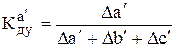Тогда для приведенной исходной мультипликативной модели:

;

;

;

.

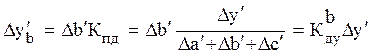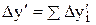Переход от относительных единиц к абсолютным осуществляется по формулам:

; .

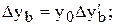
Если взаимосвязь факторов двух уровневая (n-уровневая), то необходимо рассчитывать коэффициент пропорционального деления для каждого уровня, а коэффициент долевого участия для каждого факторного показателя соответствующего уровня.

 

5.2. 6. Интегральный способ

 

Для приемов элиминирования характерны следующие недостатки:

величина влияния фактора на изменение результативного показателя зависит от места расположения фактора в детерминированной модели;

дополнительный прирост результативного показателя, полученный от совместного взаимодействия факторов, присоединяется к последнему фактору.

Интегральный метод не имеет этих недостатков. Величина влияния фактора на изменение результативного показателя не зависит от места расположения фактора в детерминированной модели. Дополнительный прирост от совместного взаимодействия факторов, распределяется между ними поровну.

Метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа .

Для мультипликативных моделей:

Исходная модель .

; .

Исходная модель

; ;

.

Исходная модель

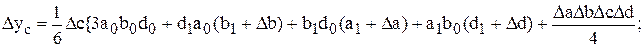
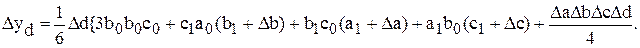
Кратная модель ; ; .

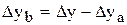Смешанная модель типа: ; ;

;	;
;	;
;	.

 

 

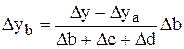5.2.7. Способ логарифмирования

 

Применяется для измерения влияния факторов в мультипликативных моделях.

Результат расчета влияния факторов на результативный показатель при этом способе не зависит от места расположения факторов в модели. Дополнительный прирост от совместного взаимодействия факторов распределяется между ними пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя.

Исходная модель

; ; .

 

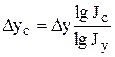Задачи к практическому занятию №5

 

Все предлагаемые в дальнейшем задачи решаются в следующей последовательности:

определяется результативный и факторный показатели;

составляется исходная и расширенная математическая модель факторной системы и определяется ее тип;

рассчитывается уровень влияния факторов на результативный показатель теми приемами, которые указаны в задаче;

проверяется правильность расчета факторов методом балансовой увязки (составляется таблица результатов влияния факторов) и делаются выводы по результатам решения задачи.

 

Задача 5.1. На основании имеющейся информации в табл.5.1 определить уровень влияния факторов на результативный показатель всеми возможными приемами.

 

Таблица 5.1 Исходные данные для факторного анализа объема произведенной продукции или среднегодовой выработки рабочего

Показатели	Обозначение	План	Факт	Абсолютное отклонение (+, –)	Выполнение плана, %
1. Произведенная продукция, тыс. грн
2. Среднегодовая численность рабочих, чел.
3. Отработано всеми рабочими за год
3.1 дней
3.2 часов
4. Количество дней, отработанных одним рабочим за год
5. Среднегодовая выработка продукции одним рабочим, тыс. грн. (стр.1:стр.2)
6. Среднедневная выработка продукции одним рабочим, грн. (стр.5:стр.4)
7. Средняя продолжительность рабочего дня, ч. (стр.3.2:стр.3.1)
8. Среднечасовая выработка продукции одним рабочим, грн. (стр.6:стр.7)

 

Задача 5.2. На основании имеющихся в табл. 5.2 исходных данных определить влияние факторов на изменение объема произведенной продукции всеми возможными способами, в том числе пропорционального деления или долевого участия. Таблица 5.2 Исходные данные для факторного анализа объема произведенной продукции или среднегодовой выработки работающего

Показатели	Обозначение	План	Факт	Абсолютное отклонение (+,–)	Выполнение плана, %
1. Произведенная продукция, тыс. грн.
2.Среднегодовая численность работающих, чел.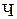
3.Среднегодовая численность рабочих, чел.
4. Удельный вес рабочих в общем объеме работающих, %		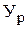80,0	80,428
5. Количество человеко‑дней, отработанных за год всеми рабочими
6.Количество человеко‑часов, отработанных за год всеми рабочими			6215794,2
7. Среднегодовая выработка продукции на одного работающего, тыс. грн. (стр.1: стр.2)	В
8. Среднегодовая выработка продукции на одного рабочего, тыс. грн. (стр.1:стр.3)
9.Количество дней, отработанных за год одним рабочим (стр.5:стр.3)
10.Средняя продолжительность рабочего дня, ч. (стр.6: стр.5)
11.Среднедневная выработка продукции на одного рабочего, грн. (стр.8:стр.9)
12. Среднечасовая выработка на одного рабочего (стр.11: стр.10)

 

 

Задача 5.3. На основании имеющихся в табл. 5.3 исходных данных проанализировать влияние использования основных производственных фондов на объем произведенной продукции способом абсолютных разниц и интегральным методом.

Таблица 5.3 Исходные данные для факторного анализа фондоотдачи

Показатели	Обозначение	План	Факт	Абсолютное отклонение (+,–)	Выполнение плана, %
1. Произведенная продукция, тыс. грн.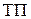
2. Первоначальная среднегодовая стоимость основных производственных фондов, тыс. грн.
3. Фондоотдача (стр.1:стр.2), грн.

 

Задача 5.4. На основании имеющихся в табл. 3.4 исходных данных проанализировать влияние факторов на изменение коэффициента оборачиваемости нормируемых оборотных средств всеми возможными приемами.

 

Таблица 5.4 Исходные данные для факторного анализа коэффициента оборачиваемости нормируемых оборотных средств

Показатели	Обозначение	План	Факт	Абсолютное отклонение (+, –)	Выполнение плана, %
1. Выручка от реализации продукции, тыс. грн.
2. Среднегодовая стоимость нормируемых оборотных средств, тыс. грн.
3. Коэффициент оборачиваемости нормируемых средств (стр.1:стр.2)

 

Задача 5.5. На основании имеющихся в табл. 5.5 исходных данных проанализировать влияние факторов на изменение прибыли от реализации изделий А всеми возможными приемами.

 

Таблица 5.5 Исходные данные для факторного анализа прибыли от реализации изделий А

Вид продукции	Количество реализованной продукции, шт.,	Цена единицы продукции, грн. /шт.,	Себестоимость единицы продукции, грн. /шт.,	Прибыль от реализации, тыс. грн..,	Абсолютное отклонение (+,–) тыс.грн.	Выполнение плана, %
план	факт	план	факт	план	факт	план	факт
А
А			508,68	526,34		412,8

 

Задача 5.6. На основании имеющихся в табл. 5.6 исходных данных проанализировать влияние факторов на изменение уровня рентабельности производства (производственных фондов) всеми возможными способами.

 

Таблица 5.6 Исходные данные

Показатели	Обозначение	План	Факт	Абсолютное отклонение (+, –)	Выполнение плана, %
1.Балансовая прибыль, тыс. грн.
2. Среднегодовая первоначальная стоимость основных производственных фондов, тыс. грн.
3. Среднегодовая стоимость нормируемых оборотных средств, тыс. грн.
4. Коэффициент рентабельности производства стр.1:стр.(2+3)

 

Задача 5.7. Проанализировать способом пропорционального деления или долевого участия влияние факторов на изменение уровня рентабельности производства. Известно, что уровень рентабельности производства в отчетном периоде снизился на 8% в связи с тем, что произошло увеличение производственных фондов предприятия на 200 тыс.., в том числе среднегодовая первоначальная стоимость основных производственных фондов увеличилась на тыс. грн., а среднегодовая стоимость нормируемых оборотных средств уменьшилась на 50 тыс. грн. Сумма балансовой прибыли предприятия в отчетном периоде по сравнению с планом не изменилась.

Практическое занятие №6

 

Тема: Способы стохастического факторного анализа. Корреляционно-регрессионный анализ

 

Теоретические материалы для решения практических задач:

Метод корреляционно-регрессионного анализа используется для определения влияния факторов, не находящихся с результативным показателем в функциональной зависимости. При корреляционной зависимости в отличие от функциональной определенному значению фактора может соответствовать несколько значений результативного показателя.

Корреляционная зависимость проявляется при большом количестве наблюдений о величине исследуемых факторов и результативных показателях.

Корреляционная зависимость проявляется при большом количестве наблюдений о величине исследуемых факторов и результативных показателях, т.к. отражает зависимости между средними их величинами.

Различают парную (однофакторную) и множественную (многофакторную) корреляцию.

Парная корреляция – это связь между двумя показателями, один из которых факторный, другой – результативный.

Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Обычно при анализе применяются простейшие прямолинейные (уравнение прямой).

Однофакторные зависимости вида

.

Многофакторные:

,

где х, , , …, — соответственно факторный и факторные показатели;

а, b, , , …, 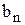— параметры уравнения регрессии, которые нужно определить;

При выборе факторов, влияющих на результативный показатель следует руководствоваться следующими положениями:

1. учитывать причинно-следственные связи между показателями;

2. отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель;

3. все факторы должны быть количественно измеримы, т.е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности;

4. в корреляционную модель линейного типа не должны включаться факторы, связь которых с результативным показателем имеет криволинейный характер или носит функциональный характер, а также взаимосвязанные факторы.

При корреляционно-регрессионном анализе решаются следующие задачи:

1. установление зависимости изменения среднего значения результативного показателя от изменения одного или нескольких факторов (в абсолютном измерении), это значит, определить на сколько единиц изменяется величина результативного показателя при изменении фактора.

В том случае мы определяем уравнение регрессии.

2. установление относительной степени зависимости результативного показателя от каждого фактора – определяем коэффициент корреляции.

При наличии многофакторной зависимости ее рассчитывают на ЭВМ по типовой программе.

Рассмотрим использование прямолинейной однофакторной (парной) корреляции

.

Значения коэффициентов а и b находят из системы уравнений, полученных по способу наименьших квадратов. В данном случае система уравнений имеет вид

где n— количество наблюдений;

а – постоянная величина результативного показателя, не связанная с изменением фактора х;

b – параметр, показывающий среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения.

Для линейной математической формы связи параметры a и b можно определить по формулам:

­_­­­

 

Значения , , 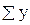, — рассчитываются на основе фактических исходных данных.

В случае прямолинейной формы связи между изучаемыми показателями коэффициент корреляции рассчитывается по формуле

Коэффициент корреляции может принимать значения от 0 до . При прямой связи он не превышает +1, а при обратной связи –1. Чем ближе его величина к 1, тем более тесная связь между изучаемыми показателями и наоборот.

Обычно считают:

|r|< 0,3 - связь слабая (нет зависимости)

0,3 ≤ |r| ≤ 0,6 - связь средняя

0,6< |r| ≤ 1 -связь сильная

Теснота связи "сильная", переходяща

Поделиться:

Воспользуйтесь поиском по сайту: