1.5. Численные методы.

В пакете MATLAB реализованы методы вычислительной математики, ориентированные на современную вычислительную технику. Особое внимание уделено методам, устойчивым к ошиб­кам округления. Все вычисления производятся с удвоенным ма­шинным словом, что повышает точность результата.

В разделе 1. 4 описаны программы определения обратной матрицы INV, нахождения всех (комплексных) корней полинома ROOTS, определения собственных чисел и собственных векторов матрицы EIG. Очень важной матричной программой является про­грамма SVD(X) разложения по вырожденным (сингулярным) значе­ниям матрицы X, алгоритм которой подробно описан в [7]. Эта функция используется для определения нормы матрицы NORM(X), числа обусловленности матрицы COND(X) и в других программах.

Для решения произвольной системы линейных уравнений

A * X = B                            (1. 1)

где A - матрица размером m x n, X - вектор-столбец неиз­вестных длиной n, а B - вектор-столбец длиной m, используется операция левого деления:

X = A\B                               (1. 2)

Для квадратной неособенной матрицы A это эквивилентно X = INV(A) * B

Если m не равно n или ранг матрицы A меньше числа неизвестных, то (1. 2) - решение недоопределенной или переопределенной системы методом наименьших квадратов: вектор решения X длиной n минимизирует сумму

( aij xj - bi)

и имеет не более k отличных от нуля компонент, где k - ранг матрицы A.

Если на вектор X накладываются ограничения вида xi > = 0 (i=1,..., n),

решение системы (1. 1) методом наименьших квадратов может быть найдено вызовом функции

X=NNLS(A, B).

Если указать два выходных аргумента

[X, W]=NNLS(A, B),

то вектор W будет иметь длину n и wi < 0, если xi = 0 и wi = 0, если xi > 0.

В MATLAB реализованы описаные в [7] алгоритмы функций FZERO нахождения нулей функции в окрестности заданного значе­ния и FMIN минимизации функции одной переменной, обеспечиваю­щие хорошую сходимость к решению. Обращение к функции FZERO для решения уравнения F(x) = 0 имеет вид:

x=FZERO('F', x0),

где строка F задает имя действительной функции одной дей­ствительной переменной x, а x0 - начальное приближение корня. Например, FZERO('sin', 3) дает результат pi. Функция F(x) может быть задана пользователем в виде M-файла, содер­жащего программу ее вычисления по заданному аргументу x (см. раздел 1. 5).

Для поиска минимума действительной функции одной пере­менной на интервале x1 < x < x2 можно обратиться к функции FMIN('F', x1, x2).

Для минимизации функции нескольких переменных предназна­чена функция FMINS, обращение к которой имеет вид:

X = FMINS('F', X0),

где X0 - вектор начальных приближений по всем переменным, строка F задает имя функции или M-файла, описывающего вы­числение функции F(X). Для решения задачи используется симплекс - метод Нелдера - Мида [8] с переменным шагом.

В обращении к функции FZERO, FMIN и FMINS можно указать два дополнительных входных аргумента, первый из которых за­дает относительную погрешность результата (значение по умол­чанию равно 0. 0001), а второй при ненулевом его значении включает печать последовательных приближений к решению на каждой итерации. Например, при выполнении

x = FMIN('sin', 2, 3, 1. 0E-5, 1)

будет определен минимум функции sin(x) на интервале (2, 3) с точностью 0. 000001, с печатью промежуточного результата на каждом шаге.

Для решения системы из n нелинейных уравнений с n неиз­вестными методом Ньютона с линейным поиском предназначена функция FSOLVE. Уравнения имеют вид:

Fi(x1,..., xn) = 0            (i=1,..., n).

Например, для решения системы из трех уравнений

sin(x) + y^2 + log(z) - 7 = 0

3*x + 2^y - z^3 + 1 = 0

x + y + z - 5 = 0

нужно выполнить X = FSOLVE('xyz', [1 1 1]'), где xyz -следующий M-файл:

function q = xyz(p)

x = p(1); y = p(2); z = p(3);

q = zeros(3, 1);

q(1) = sin(x) + y^2 + log(z) - 7;

q(2) = 3*x + 2^y - z^3 + 1;

q(3) = x + y + z - 5;

Он содержит программу вычисления указанных выше функций xyz(P) для любого вектора аргументов P длиной три.

В обращении могут быть указаны дополнительные входные и выходные аргументы

[X, CODE, PATH] = FSOLVE('F', X0, DETAL, FPAR, 'JAC', SCALE). Выходной аргумент CODE указывает код завершения задачи, он равен 1 при нормальном окончании и в этом случае X - вектор решения, PATH - матрица последовательных приближений к решению.

Вектор DETAL состоит из элементов, определяющих режимы алгоритма и допустимые погрешности при вычислении функций и их градиентов. Если можно задать аналитический способ вычисле­ния матрицы Якоби системы уравнений, то есть матрицы

| dfi/dxj |           (i, j = 1,..., n),

то JAC - строка, указывающая имя М-файла, содержащего прог­рамму его вычисления. В этом случае четвертый элемент вектора DETAL должен быть равен 1. FPAR - множество дополнительных па­раметров (констант), которые могут передаваться функциям F и JAC в качестве второго аргумента. Если дополнительные парамет­ры FPAR передаются, то пятнадцатый элемент вектора DETAL должен быть задан равным 1. SCALE - матрица из двух столбцов, содержащих типичные ненулевые значения аргумента X в первом столбце и функции F - во втором столбце, предназначенная для целей масштабирования. В этом случае шестнадцатый элемент вектора DETAL должен быть равен 2, при его значении равном 1 масштабирование осуществляется по начальным значениям аргумен­тов X0 и функций F(X0). Из других элементов вектора DETAL отметим двенадцатый, задающий число достоверных десятичных знаков при вычислении функций F(X), и третий, значения которо­го (0 или 1) определяют способ аппроксимации матрицы Якоби.

Все вектора в обращении к FSOLVE должны быть столбцами. Подробно алгоритм этой функции описан в [9], где можно найти и рекомендации по выбору параметров.

Для решения системы дифференциальных уравнений вида

dyi/dt = fi(t, y1,..., yn)

при начальных условиях yi(t0) = yi0              (i=1,..., n)

предназначены функции ODE23 (метод Рунге-Кутта 2-го и 3-го порядка) и ODE45 (тот же метод 4-го и 5-го порядка) [10, 11].

Обращение к обеим функциям одинаково и имеет вид:

[T, Y] = ODE23('F', t0, tk, Y0),

где F - имя M-файла, содержащего описание программы вычис­ления функций fi, t0 и tk - задают интервал интегрирования, вектор Y0 - начальные значения искомых функций. Результатом будет вектор-столбец T точек интегрирования и матрица Y, каждая строка которой содержит значения всех функций yi для соответствующих значений вектора T. Для построения гра­фиков решений можно вызвать функцию PLOT(T, Y).

Программа в M-файле F должна вычислять функцию вида YP = F(t, Y), где t - скаляр, Y - вектор-столбец значений искомых функций yi, YP - вектор-столбец значений производных dyi/dt. Погрешность решения по умолчанию равна 0. 0001, можно задать другое значение при обращении

[T, Y] = ODE23('F', t0, tk, Y0, tol, trace).

Если задан ненулевой последний аргумент, на экран выводится информация по каждому шагу интегрирования.

Для вычисления определенного интеграла

можно воспользоваться функцией QUAD, которая реализует метод Симпсона [10, 11], или функцией QUAD8, в которой исполь­зуется метод Ньютона-Котеса. Функция f(x) может быть комплекснозначной функцией действительного аргумента. Обращение имеет вид:

Q = QUAD('F', a, b),

где F - имя подинтегральной функции или М-файла. Программа вычисления Y = F(X) должна допускать использование в качестве аргумента X вектора из значений на множестве точек xi, в этом случае Y должен быть вектором значений подинтег­ральной функции в соответствующих точках.

При обращении

Q = QUAD('F', a, b, tol, trace)

используется точность tol, а при ненулевом значении trace на экране последовательно точками изображается график дейст­вительной части подинтегральной функции f(x) и знаками '+'- график ее мнимой части, иллюстрируя тем самым процесс вычис­ления интеграла.

Функции SPLINE и INTERP2 осуществляют интерполяцию функ­ции одной переменной кубическими сплайнами [10] и бигармо­ническими функциями. Если обращение имеет вид

Yi = SPLINE (X, Y, Xi) или Yi = INTERP2(X, Y, Xi),

где X и Y - вектора данных значений аргумента и функции, а Xi - вектор новых значений аргумента, то вектор Yi будет со­держать вычисленные значения функции в точках, заданных век­тором Xi.

Если в обращении к фукнкции SPLINE указано только два входных аргумента

PP = SPLINE (X, Y),

то вектор-строка PP будет содержать информацию об узлах X и коэффициентах P интерполяционных полиномов в следующем виде:

PP = [n, x0, x1,..., xn, k, p11,..., p1n, p21,..., p2n, ............, pk1,..., pkn].

Здесь n - количество заданных промежутков, k < = 4 - коли­чество коэффициентов интерполяционных полиномов, pij - i-ый коэффициент интерполяционного полинома для j-го про­межутка. Вычислить значения функции в точках, заданных вектором Xi можно, выполнив команду

Yi = PPVAL(PP, Xi).

Весьма полезной может быть функция RESIDUE, предназначен­ная для вычисления вычетов простых и кратных полюсов дробно­рациональной функции. Она может использоваться, например, для выполнения аналитически обратного преобразования Лапласа с по­мощью таблиц этого преобразования для элементарных функций. Если B(s) и A(s) - полиномы с постоянными коэфиициентами, то при обращении

[R, P, K] = RESIDUE(B, A)

определяютя вычеты, полюса и свободный член в разложении на простые дроби отношения двух полиномов

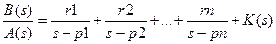
Вектора B и A задают коэффициенты полиномов по убывающим сте­пеням s. Вычеты располагаются в виде вектора-столбца R, соот­ветствующие полюса - в виде вектора-столбца P такой же длины, а свободный член - в виде вектора-строки K коэффициентов поли­нома по убывающим степеням s.

Если полюс pi имеет кратность k, то он в столбце P будет указан k раз, а соответствующие вычеты будут располагаться в порядке возрастания степени (s - pi). Для полиномов с действи­тельными коэффициентами паре комплексно-сопряженных полюсов pm+i*qm и pm-i*qm соответствует пара комплексно-сопряженных вычетов rm+i*zm и rm-i*zm.

При обращении [B, A] = RESIDUE(R, P, K)

представление в виде простых дробей преобразуется обратно к виду B(s)/A(s).

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: