 |
Согласно задания, схема на рисунке 4 должна быть удвоенна. Так же добавим в схему источник питания, сопротивление нагрузки и землю. Преобразованная схема изображена на рисунке 5.
|
|
|
|
 | |||||
 | |||||
 | |||||
Yг C RH
 |
Рисунок.5. Преобразованная схема низкочастотного фильтра.
Построим граф для нашего фильтра.
1 4 2 5 3
1 2 3
Рисунок.6. Граф низкочастотного фильтра.
Топологические элементы схемы: ветвей дерева – 3 (1,2,3); узлов – 3 (1, 2, 3); сечений – 3; контуров – 2, хорды- 2 (4,5).
2.3. Составим топологические матрицы [А],[П],[Г]:
Составим матрицу [А]
1 0 0 -1 0
[А] = 0 1 0 1 -1
0 0 1 0 1
Матрицу сечений [П]
1 0 0 -1 0
[П] = 0 1 0 1 -1
0 0 1 0 1
Как видим матрицы [А] и [П] аналогичны, так как число сечений равно числу узлов.
Матрицу контуров [Г]
1 -1 0 1 0
[Г] = 0 1 -1 0 1
2.4. Запишем связь напряжений ветвей с напряжениями сечений:
1 0 0 U1
0 1 0 U 1 U2
[П] t [U] = 0 0 1 ´ U 2 = U3 = [U с ]
-1 1 0 U 3 U2-U1
0 -1 1 U3-U2
2.5. Запишем второй закон Кирхгофа в матричном виде
1 0 0
0 1 0 U 1
[Г] [U в ] = [Г] [П] t [U] = 1 -1 0 1 0 ´ 0 0 1 ´ U 2 =
0 1 -1 0 1 -1 1 0 U 3
0 -1 1
U 1 - U 2 + U 2 - U 1 0
U 2 - U 3 + U 3 - U 2 = 0
|
|
|
2.6. Найдём матрицу проводимости и ММС тремя способами:
2.6.1. формальным способом: матрица [Y] записывается в виде квадратной матрицы методом узловых потенциалов. Элементы главной диагонали являются проводимостью соответствующих ветвей, а остальные элементы проводимость элементов, которые входят, как в один, так и в другой контур.
 |  | | |
[Y]=
2.6.2. По компонентным уравнениям
Запишем по второму закону Кирхгофа систему уравнений относительно неизвестных контурных токов:
По первому узлу:
IB1+IB4=Iг
IB1=Yг*UB1; IB4=2/pL*(U2-U1); тогда
(Yг+2/pL)*U1-2/pL*U2 =Iг
По второму узлу:
IB4+ IB2- IB5=0
-2/pL*U1+(4/pL+pC)U2-2/pL* U3=0
по третьему узлу:
-2/pL*U3+(1/RH+2/pL)U3=0
Проведя преобразования получим коэффициенты при токах дадут нам матрицу проводимости [Y]:
 |
[Y]=
 |
2.6.3.Перемножаем матрицы [Y] = [П] [Y в ] [П] t.
1/R г 0 0 0 0
1 0 0 -1 0 0 2/pL 0 0 0
[Y] = [П] [Y в ] [П] t = 0 1 0 1 -1 ´ 0 0 pC 0 0 ´
0 0 1 0 1 0 0 0 2/pL 0
0 0 0 0 1/ R н
| | | |  | | |
1 0 0
0 1 0
´ 0 0 1 =
-1 1 0
0 -1 1
Полная математическая модель схемы для данного фильтра метода узловых потенциалов будет иметь вид:
|
|
|
U 1 I г
´ U 2 = 0
U 3 0
2.7. Запишем коэффициент передачи фильтра по току: К I = I вых /I вх = I 3 /I 1 через алгебраические дополнения матрицы [Y]:
I 3 А 13 М 13
К I = ____ = ______ = _______
I 1 А 11 М 11
Определим миноры матрицы проводимости [Y]:
4 /pL +pC -2/pL
М 11 = = 
= 
-2/pL 1/R н + 2/pL
-2/pL 4/pL +pC
М13 = = 
0 -2/pL
Заменим оператор символического преобразования p на jw, заменим w=2p¦=
2*3.14*3.2=20.1*103 Гц
М13=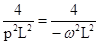 
= 
М11=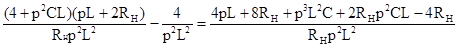 
=
= 
=
= 
=
= 
Произведём деление и запишем К I в виде дроби? произведём умножение числителя и знаменателя на комплексно-сопряжённое к знаменателю, чтобы избавиться от мнимого числа в знаменателе. Подставим в полученное выражение численные данные параметров:
К I =
В показательной форме коэффициент передачи будет иметь вид:
К(w) = 
» 
j(w) = arctg Im/Re = arctg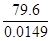 
=90
КI = К(w)еjj(w)» 79.6 
Вывод
Рассмотрев данную курсовую работу, мы научились пользоваться методами анализа линейных и реальных цепей. Были кратко рассмотрены матричные методы представления математической модели схемы, описан топологический метод описания схем, дуализм, при рассмотрении схем. Использовано символическое изображение времени. Была дана краткая классификация фильтров и мы рассмотрели возможность их представления линейными цепями с постоянными параметрами.
В практической части мы научились рассчитывать передаточную характеристику низкочастотного фильтра методом узловых потенциалов, с применением символического преобразования времени. А также изобразили амплитудно-частотную характеристику с указанием расчётной точки.
|
|
|
Приложение А
Амплитудно-частотная характеристика низкочастотного фильтра.
¦
Рисунок.1. амплитудно-частотная характеристика Т-образного
низкочастотного фильтра.
Распространенные типы преобразований и данных значения величины p.
Таблица 1
| Тип преобразования | Характер функции времени | Прямое преобразование | Обратное преобразование | Оператор р |
| Символическое преобразование | Гармоническая функция ¦(t)=Acos(w+a) | A=Aeja=a+b
A= 
a=arctg 
| ¦(t)=Re[Aejwt] | p =jw w=const |
| Ряд Фуре | Периодическая функция
¦(t)= ¦(t+T)
T= 
|
Ak= Ake-j ak=
= 
| ¦(t)=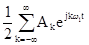 
| p =jkw1 (k=1,2,3…) |
| Интеграл Фурье | Непериодическая
функция
|
S(jw)=S(w)eja(w)=
= 
| ¦(t)= 
| p =jw -∞≤w≤∞ |
| Преобразование Лапласа | Непериодическая функция ¦(t)=0 при t<0 | F(p)= 
F(p)=L[¦(t)]
| ¦(t)= 
¦(t)=L-1[F(p)]
| p=σ+j∞ σ=Re [p]> σ0 |
Список литературы.
1. Сигорский В.П. Основы теории электронных цепей – К.: Техника,
1967. – 610с.
2. Арестов К. В. Основы электроники – М.: Радио и связь, 1988. – 272 с.
3. Бакалов В. П. Основы теории электрических цепей и электроники – М.: Радио и связь, 1989. – 526с.
4. Матханов П. Н. Основы анализа электрических цепей – М.: Высшая школа, 1986. – 528с.
|
|
|
