 |
Оптимизация иерархических структур
|
|
|
|
Вопросы о целесообразности использования иерархических структур
Выясним условия, при которых целесообразно применение иерархической структуры для решения задачи управления заданной сложности Q.
Пусть состояние объекта управления характеризуется контролируемыми переменными, и пусть сложность задачи управления объектом есть некоторая функция числа этих переменных.
Тогда исходная сложность задачи управления есть
(1.3.1.)
В соотношении (1.3.1.) учитывается вся информация об объекте управления, что соответствует использованию централизованной структуры управления. Если исходная сложность задачи управления превосходит уровень 1-го информационного барьера, то необходимо перейти к структуре, обладающей чертами децентрализации. Используя децентрализованную структуру мы можем достигнуть второго информационного барьера, и, учитывая недостатки данных структур, необходимо переходить к иерархическим структурам.
Посмотрим, при каких условиях целесообразно использовать иерархическую структуру.
Рассмотрим трехуровневую иерархическую структуру с минимальным числом центров на каждом уровне (см. рисунок 1.3.3), и пусть центры одного уровня решают задачи одинаковой сложности.
Пусть далее центр нижнего уровня передает центру верхнего уровня часть информации α·j, где 0 < α < 1.
Очевидно, каждый центр 1-го уровня имеет дело с информацией. Объем которой n/4. Сложность задачи, которую решает каждый центр 1-го уровня есть
(1.3.2.)
Каждый центр 2-го уровня имеет дело с информацией, объем, которой 
, а сложность задачи центра 2-го уровня есть
(1.3.3.)
Центр 3-го уровня имеет дело с информацией, объем которой 
, а сложность решаемой центром задачи
|
|
|
(1.3.4.)
Суммарная сложность задачи, решаемой всеми центрами иерархической структуры, равна
(1.3.5.)
Введение иерархической структуры целесообразно, если суммарная сложность решаемой структурой задачи Q* меньше исходной сложности задачи управления, т.е., если выполняется соотношение
Q* < Q = F(n) (1.3.6.)
Смысл соотношения (1.3.6.) в том, что введение иерархической структуры не увеличивает способность центров и всей структуры к переработке информации, но снижает сложность задач, решаемых центрами и всей структуры в целом.
Посмотрим, при каких условиях имеет место соотношение (1.3.6.)
Пусть сложность задачи управления есть линейная функция n,т.е.
F(n) = b n (1.3.7.)
Тогда выражение (1.3.5.) можно переписать в виде
(1.3.8.)
Поскольку величина 
> 1, то
Q* > Q = F(n) (1.3.9.)
и использование иерархической структуры нецелесообразно, т.е. если сложность задачи управления зависит линейно от числа n, иерархическая организация структуры управления не имеет смысла, т.к. в этом случае суммарная сложность задачи Q* превосходит исходную сложность Q.
Пусть теперь сложность задачи управления есть квадратная функция числа переменных n, т.е.
F(n) = b n2 (1.3.10.)
что соответствует реальному положению вещей (см. §1-2).
Тогда выражение (1.3.8.) можно записать в виде
(1.3.11.)
При условии
(1.3.12.)
Справедливо соотношение
Q* < Q = F(n) (1.3.13.)
И, следовательно, использование иерархической структуры целесообразно, т.е. суммарная сложность задачи, решаемой всеми центрами структуры, меньше исходной сложности задачи управления Q = F(n). Соответствующим выбором значения α можно регулировать значенияQ`, Q`` и Q```, удерживая их ниже уровня 1-го информационного барьера, хотя исходная сложность задачи управления Q = F(n) может существенно превосходить уровень 1-го информационного барьера для централизованной структуры управления. Определим, какова максимальная часть информации, которую можно передавать с нижнего уровня на верхний, не нарушая условия (1.3.12.). Максимальное значение αmax найдем из условия .
|
|
|
Откуда α2 =0,65 и, следовательно, αmax = 0,80. Таким образом, введение иерархической структуры целесообразно, когда сложность задачи управления растет быстрее, чем линейная функция от n, и вверх по иерархии передается упрощенная модель задачи управления.
Что существенно при такой структуре управления? Ходом технологического процесса управляет технолог производства (черты централизации), однако, значение управляющих воздействий определяет не он.
Управляющие воздействия вырабатываются нижним уровнем на свое усмотрение (черты децентрализации), но в пределах ограничений, определяемых директивными указаниями верхнего уровня.
Если бы технолог производства был в состоянии воспринять и переработать всю необходимую для управления процессом информацию, возможно, он определил бы другие значения управляющих воздействий, отличные от тех, которые выбрал оператор. И управляющие воздействия технолога производства в целом обеспечивали бы более оптимальное управление процессом, поэтому мешает 1-ый информационный барьер.
Поэтому, введя иерархическую структуру управления, мы несколько теряем в оптимальности управления, но зато: а) получаем возможность решать задачу управления большой сложности; б) получаем устойчивое и надежное управление, в целом близкое к оптимальному.
Надежность иерархических структур обусловлена тем, что отказ одного центра не приводит к отказу всей системы, как скажем, в случае централизованной структуры, а только к некоторому снижению эффективности ее функционирования.
Эта особенность структуры дает наибольший эффект в тех случаях, когда соседние центры способны взять на себя функции вышедшего из строя центра, что связано с развитыми свойствами адаптации и самоорганизации и присуще структурам организационного управления. Это качество иерархических структур называется живучестью.
Оптимизация иерархических структур
Рассмотрим вкратце задачу оптимизации иерархической структуры, т.е. задачу определения оптимального количества уровней иерархии и оптимального количества центров на каждом уровне, обеспечивающих решение задачи управления сложности Q с заданным качеством.
|
|
|
Важными характеристиками иерархической структуры в решении этой проблемы являются степень централизации и норма управляемости. Для каждой пары смежных уровней 
степень централизации 
измеряется отношением суммарной сложности задач Qi, решаемых на i-м уровне, к суммарной сложности задач Qi-1, решаемых на i-1-ом уровне, т.е.
(1.3.14.)
Степень централизации структуры в целом определяется выражением:
(1.3.15.)
где ai – некоторые весовые коэффициенты.
γ определяется значением α:
γ = f (α)
· Смещение основной массы решаемых задач в сторону высшего уровня отождествляется с повышением качества управления при увеличении количества перерабатываемой информации на верхних уровнях (т.е. 
) (повышение степени централизации).
· Смещение решений в сторону нижних уровней (понижение степени централизации) соответствует увеличению самостоятельности центров нижних уровней и обычно связано с уменьшением оптимальности управления (т.е. 
).
Введем понятие стоимости Сγ решения задачи управления. Стоимость Сγ определяется затратами на функционирование структуры Сγ1 и потерями Сγ2 за счет ухудшения качества управления:
Сγ = Сγ1 + Сγ2
Очевидно, что Сγ1, Сγ2 и суммарная стоимость Сγ являются функциями степени централизации γ, что изображено графически на рисунке 1.3.4.
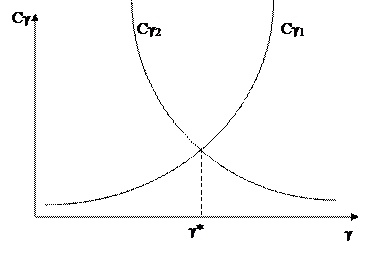
Рисунок 1.3.4.
Тогда γ* определяет оптимальное значение степени централизации структуры с точки зрения суммарных потерь на решение задачи управления заданной сложности Q. Понятие степени централизации тесно связано с другой характеристикой, определяющей оптимальность иерархической структуры – нормой управляемости.
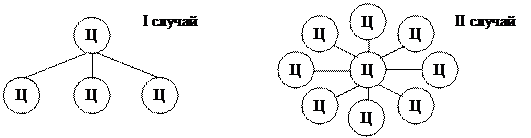Норма управляемости ι определяет количество центров нижележащего уровня, подчиненных данному центру. Другими словами, норма управляемости определяет количество центров, которыми может эффективно «управлять» верхний центр при данной степени централизации γi. Например, проведенные исследования показали, что в научных организациях в среднем оптимальное соотношение между руководителем и его сотрудниками составляет 1:5.
|
|
|
I случай: центр не перегружен и даже не догружен. Количество уровней увеличивается.
II случай: вышестоящий центр перегружен. Количество уровней будет уменьшаться.
Qι – стоимость принимаемого решения определяется стоимостью функционирования структуры Q1ι и потерями за счет неоптимальности принимаемого решения Q2ι.
Qι = Q1ι + Q2ι
Если 
, то количество уровней будет уменьшаться 
.
Если 
, то количество уровней будет увеличиваться 
. (См. рис. 1.3.5)
Рисунок 1.3.5.
ι* – оптимальное значение, при котором минимальна стоимость принимаемого решения.
Q = Qγ + Qι↓
Определение степени централизации и нормы управляемости – очень важная и вместе с тем трудная проблема синтеза оптимальной иерархической структуры. Существующая в настоящее время теория не позволяет решить ее в общем виде.
Выводы:
Во-первых, если нет ограничений, нельзя улучшить качество решения задачи управления за счет увеличения уровней иерархической структуры (предполагается, что существует структура, которая достаточно качественно решает задачу управления, повышать качество нельзя, увеличивается количество уровней).
Во-вторых, необходимо стремиться минимизировать число центров на каждом уровне. Тогда задача оптимизации иерархической структуры с минимальным количеством уровней и минимальным количеством центров на каждом уровне, обеспечивающей заданное качество решения задачи управления сложности Q.
Q = Qγ + Qι↓ => минимизация α и Qι.
|
|
|
