 |
Открытие рычага. Центр тяжести. Закон рычага
|
|
|
|
Открытие рычага
Первым научным исследованием Архимеда в механике было доказательство закона рычага.
Люди применяли рычаги с незапамятных времен и умели ими искусно пользоваться. На постройках египетских пирамид рабы втаскивали тяжелые камни наверх при помощи рычагов. Судостроители ставили мачты на кораблях рычагами. Воду из колодцев доставали, пользуясь журавлем, то есть рычагом с противовесом. Римляне взвешивали товары на художественно изготовленных рычажных весах – безменах. Корабли древних приводились в движение веслами и имели рулевое управление, а руль и весла– тоже рычаги.
Рычаг, ворот, блок и зубчатые колеса были известны людям задолго до Архимеда. Техники знали, что с помощью этих простых машин можно малой силой двигать большие тяжести. Но объяснить, почему рычаг или ворот позволяет сделать это, никто не мог.
Ученые наблюдали, как рабы на постройке налегают всем телом на длинные плечи рычагов. Приподнимаемая ими каменная глыба покачивалась и медленно двигалась на предназначенное ей место. А эти глыбы не так‑ то уж малы. Каждый камень, из которых сложена величайшая из пирамид Египта, весит две с половиной тонны! Такие камни рабы вручную поднимали по уступам пирамиды на высоту пятидесятиэтажного дома! Техники не думали о том, почему рычаг позволяет малой силой поднимать большие тяжести. Когда же этот вопрос стали обсуждать философы, то они решили, что дело тут в «волшебных свойствах» круга, потому что концы рычага во время работы движутся по дугам окружностей.
Вот что писал об этом один из учеников философа Аристотеля:
«Окружность одновременно выпукла и вогнута. Каждая точка окружности – начало и конец. Продвижение по кругу – это движение вперед и одновременно назад. Пути, описываемые концами рычага, – круговые, отсюда происходят его чудесные свойства».
|
|
|
Объяснение, безусловно, замысловатое. Но философы того времени часто прибегали к таким умозрительным объяснениям явлений природы. Вместо наблюдений и опытов они наделяли вещи разными «чудесными свойствами».
Центр тяжести
Архимед не приписывал «волшебных свойств» кругу. Он знал, что явления природы объясняются естественными причинами. Такое объяснение действия рычага и хотел найти Архимед.
Простейший рычаг – это металлический или деревянный стержень. Если его подпереть в середине, то стержень останется в равновесии. Когда к концам рычага подвешены одинаковые грузы, то равновесие не нарушится. Но если на один конец рычага подвешен большой груз, а на другой – маленький, то рычаг выйдет из равновесия: одно его плечо опустится, а другое поднимется. Чтобы равновесие восстановилось, нужно опору передвинуть к большому грузу.
Архимед понял, что у рычага есть точка, в которой как будто собрана вся тяжесть грузов. Если рычаг подперт в этой точке, он сохраняет равновесие.
Эту точку Архимед назвал центром тяжести. Он исследовал условия равновесия других тел и доказал, что у каждого из них есть центр тяжести.
Тело, подпертое в центре тяжести, сохраняет равновесие при любом положении. У хорошо сделанного колеса центр тяжести – в отверстии ступицы. Поэтому колесо, насаженное на ось, находится в безразличном равновесии: как его ни поворачивай, оно сохраняет то положение, в каком его остановили. Этим пользуются, когда проверяют, хорошо ли уравновешено велосипедное колесо. Оно должно вращаться очень легко, но, когда его останавливают, колесо не должно поворачиваться само по себе.
Закон рычага
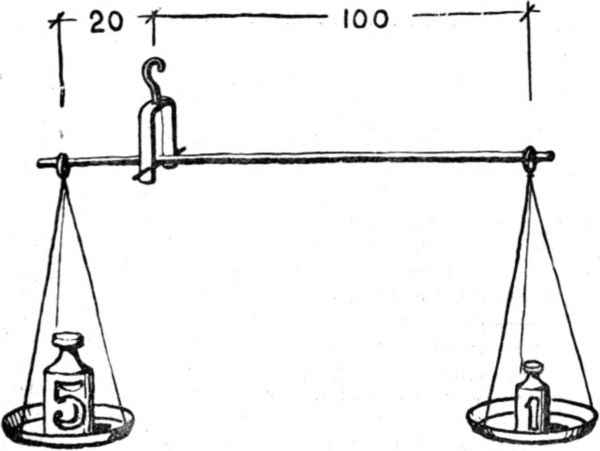
Архимед установил закон равновесия рычага: «плечи обратно пропорциональны силам (грузам)». Иначе говоря, длинное плечо должно быть во столько раз больше короткого, во сколько раз малый груз легче тяжелого. Например, пусть одно плечо рычага имеет в длину 20 сантиметров, а другое – впятеро больше–100 сантиметров. Тогда на короткое плечо можно подвесить 5 килограммов, а на длинное – только 1 килограмм, и рычаг останется в равновесии.
|
|
|
Это правило можно выразить другими словами: «произведения длины плеч на приложенные к ним силы равны между собой». Действительно, при взятых нами размерах плеч рычага и грузах:
5 X 20 = 1 X 100.
Однако рука, держащая длинное плечо рычага, описывает больший путь, чем конец короткого плеча. Пути, пройденные концами рычага, тоже обратно пропорциональны силам. Если конец длинного плеча пройдет расстояние в полметра, то короткое плечо – только 10 сантиметров. Пятикратный выигрыш в силе сопровождается пятикратным проигрышем в расстоянии.
|
|
|


