Вопрос 8 Математическое моделирование стр 36

В редакции выдающегося математика А.Н.Тихонова. "Математическая модель - приближённое описание, какого - либо класса явлений внешнего мира, выраженное с помощью математической символики. Процесс математического моделирования можно подразделить на четыре этапа.

1. Формулирование законов, связывающих основные объекты модели. Этот этап завершается записью в математических терминах, сформулированных качественных представлений о связях между объектами модели;

2. Исследование математических задач, к которым приводят математические модели. На этом этапе решается прямая задача, то есть получение теоретических следствий для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений;

3. Выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики (в пределах точности наблюдений). Если математическая модель такова, что ни при каком выборе своих характеристик не способна удовлетворить критерию практики, то эта модель непригодна для исследования данного явления. На этом этапе решается обратная задача, то есть находятся характеристики модели (параметрические, функциональные) таким образом, чтобы расчётные значения в пределах точности наблюдений совпадали бы с результатами измерений;

4. Последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели, опирающаяся на вновь полученные сведения.

Какова бы ни была природа рассматриваемой системы, её проблематика включает область проблем, от допускающих формализацию в виде задач математического программирования (такая постановка называется «жесткой»), до проблем не формализуемых, выраженных на естественном языке (такая постановка называется «рыхлой», а модели - «диффузными»). Естественно эти проблемы следует рассматривать по-разному, но в практике системного анализа имеется тенденция сводить все проблемы к одному типу, пользуясь правилом: Исследовать «рыхлую» проблему как «жесткую» гораздо опаснее, чем наоборот.

Имитационная модель – это формальное описание логики функционирования исследуемой системы и взаимодействия, отдельных её элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, и обеспечивающие проведение статистических экспериментов. Для имитационных моделей отсутствуют ограничения на область применения, наибольший эффект достигается при исследовании сложных систем, на функционирование которых существенное влияние оказывают большое количество случайных факторов.

Вопрос 9.Вариационный принцип. Системные инварианты

При описании систем постоянно употребляют превосходную степень прилагательных (наибольший эффект, наименьшие затраты, максимальная интенсивность). Это позволяет в сжатой форме выразить принцип, охватывающий широкий круг явлений. Математическая формулировка принципа содержащего прилагательное в превосходной степени обычно состоит в том, что интеграл от некоторой функции характерной для рассматриваемой системы принимают наибольшее и наименьшее значение при действительной эволюции по сравнению с любыми другими возможными способами эволюции.

Подынтегральное выражение является функцией, характеризующей рассматриваемую систему. Пусть некоторая система описывается набором показателей, зависящих от времени:

, где - номер показателя, .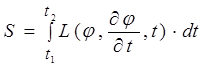

Теорема:

Если выполняется: на действительной траектории, то эволюция системы в пространстве показателей описывается уравнениями Эйлера-Лагранжа:

В механике L называют функцией Лагранжа или кинетическим потенциалом, функционал S называют «действие». Физически функция Лагранжа это: , где T и U это кинетическая и потенциальная энергия, размерность действия в этом случае .

Все системы, которые подчиняются уравнению с лагранжианом , называются лагранжевыми системами. Кроме этого вариационного принципа известны также другие, например два фундаментальных принципа, являющихся основой современной термодинамики:

1. Вариационный принцип Гиббса:

В состоянии термодинамического равновесия изолированная система имеет максимальную энтропию для всех возможных состояний с заданным уровнем энергии.

2. Вариационный принцип Пригожина:

Стационарное состояние системы, в которой происходит необратимый процесс, характеризуется тем, что скорость возникновения энтропии имеет минимальное значение при заданных внешних условиях препятствующих достижения равновесия.

Системные инварианты

Существует комбинация показателей, которая зависит только от начальных условий и не меняется в процессе движения:

Такие функции называются инвариантами. Наиболее общим инвариантом является система единиц, которая используется при описании объекта. В физических явлениях существуют фундаментальные инварианты, которые определяют структуру пространства и времени. К таким инвариантам относятся масса, энергия, импульс, заряд. Все эти величины определяют некоторые законы сохранения (закон сохранения массы, энергии, импульса, заряда), а значение их состоит в том, что они ограничивают набор разрешенных состояний системы.

Наиболее просто эти инварианты выражаются для системы точек, находящихся в силовом поле. В таблице 1 приведены эти инварианты.

Таблица 1. Законы сохранения механики точек.

№ п/п	Наименование	Выражение	Определяемое свойство
	Закон сохранения энергии		Однородность времени
	Закон сохранения импульса		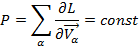Однородность пространства
	Закон сохранения момента импульса		Изотропия пространства

Во многих энергетических машинах используется непрерывный поток рабочего тела. Поток рабочего тела может обмениваться с окружающей средой теплотой и совершать работу при этом изменяется как внутренняя энергия рабочего тела, так и его механическая энергия. Уравнения динамики потоков составляются на основе уравнений сохранения массы, энергии и количества движения. Все они имеют общий вид

Накопление в объёме = Приток – Сток.

Вопрос 10.если схему нарисуете то описание не надо