 |
Системы линейных уравнений
|
|
|
|
КУРСОВАЯ РАБОТА
Тема: «Решение системы линейных уравнений методом Крамера»
Выполнила студентка
Краснова Анастасия Сергеевна
Научный руководитель
Мантуленко А.В.
Тольятти
Содержание
Введение
Глава 1. Решение линейных уравнений в программировании
Линейные уравнения
Системы линейных уравнений
Метод Крамера
Примеры
1.3 Delphi
Циклы с параметром
Условные операторы
Массивы
Переменные и их типы
Компонент Delphi StringGrid
Компонент Delphi Edit
Щелчок мыши и его обработка
Программа
Список литературы
Введение
Среда программирования Delphi в настоящее время является одной из самых развитых систем визуального объектно-ориентированного программирования. Её возможности отвечают высоким требованиям и подходят для создания приложений любой сложности. Структурированность и простота Delphi делает его одним из совершенных языков программирования.
Везде говориться о стремительном росте информационных технологий. И действительно этот темп впечатляет. Парк персональных компьютеров постоянно увеличивается. Еще с большей скоростью растет число людей использующих компьютер в своей работе.
Для овладения искусством программирования необходима практика. А это значит, только самостоятельно составляя программы можно стать профессионалом своего дела - программистом. Только практика и сопутствующие ошибки могут научить разбираться в программировании.
Научившись хорошо программировать Вы будете на «ты» со своим компьютером. А это в свою очередь залог востребованности на рынке труда и роста карьеры.
Также создание определённой программы может помочь в учёбе. Например составление программ по вычислению различной сложности уравнений и других математических задач. В данной работе рассказывается о программе по вычислению систем линейных уравнений методом Крамера.
|
|
|
Глава 1. Решение линейных уравнений в программировании
Линейные уравнения
программный линейное уравнение крамер
Линейным уравнением называется уравнение вида ax + b = 0, где x - переменная, a и b - некоторые действительные числа.
Условия:
Если a = b = 0, то решением уравнения ax + b = 0 является любое число.
Если a = 0 и b ≠0, то уравнение корней не имеет.
Если a ≠0, то уравнение ax + b = 0 называется линейным и имеет ровно одно решение x= −ab.
- Пример 1. Решите уравнение x = 5.
Решение. Корнем этого уравнения является число 5, поскольку при подстановке вместо x этого числа получается верное числовое равенство. Ответ. 5.
- Пример 2. Решите уравнение 0x+1=0.
Решение. Имеем: 0x+1=0 
1=0. Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство 1 = 0 не имеет место.
Ответ. Нет решений.
- Пример 3. Решите уравнение 0x+1=1.
Решение. Имеем 0 
x+1=1 1=1. Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство 1 = 1 является верным.
Ответ. x - любое число [2].
Системы линейных уравнений
Опр. Системой линейных алгебраических уравнений, содержащей m уравнений с n неизвестными, называется система вида
,
Рис.1 Система линейных уравнений
Здесь 
- количество уравнений, а 
- количество неизвестных.
где числа aij (i=1,2,…,m, j-1,2,…, n) называют коэффициентами системы; числа bi - свободными членами.
Числа xi являются неизвестными.
Такую систему удобно записывать в матричной форме A ∙ X = B.
Здесь А - матрица коэффициентов системы (основная матрица). Х и В - это матрицы-столбцы неизвестных и свободных членов соответственно:
|
|
|
Рис. 2 Матричная форма записи
Опр. Решением системы называется n значений неизвестных x1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы превращаются в верные равенства.
Система называется совместной <http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D0%B2%D0%BC%D0%B5%D1%81%D1%82%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9>, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система называется определённой <http://ru.wikipedia.org/w/index.php?title=%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D1%91%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9&action=edit&redlink=1>, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой [2]. 5
Метод Крамера
Опр. Метод Крамера (правило Крамера) - способ решения квадратных систем линейных алгебраических уравнений <http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9> с ненулевым определителем <http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B8%D1%82%D0%B5%D0%BB%D1%8C> основной матрицы <http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)> (причём для таких уравнений решение существует и единственно).
Описание метода.
Для системы 
линейных уравнений с неизвестными
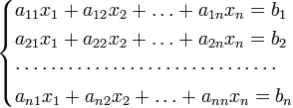
Рис. 3
с определителем матрицы системы 
, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
[1].
Примеры
Система линейных уравнений:
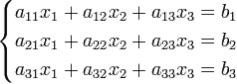
Определители:
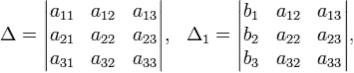
Решение:
Пример:
Решение:
). Запишем в матричной форме:
A = 
, X = 
, B = 
.
). Выясним, является ли матрица А невырожденной:
,
матрица невырожденная, значит имеет обратную.
). Вычислим алгебраические дополнения к элементам матрицы А:
А11 = -3; А21= -1;
А12=-7; А22=2. 7
). Составим обратную матрицу А-1:
А-1 = -1/13∙А* = 
). Решением матричного уравнения будет матрица Х: Х = А-1∙В.
|
|
|
Х = 
= 
Ответ: {(1;1)} [1].
Наглядное решение и разбор примеров позволит лучше понять, как составлять программу в Delphi, как будет выглядеть её структура, составить алгоритм.
Delphi
Цикл с параметром
Для составления программы важно понимать её составляющую, корсет, структуру. Знать, какие операторы и циклы необходимо использовать, чтобы программа адекватно работала.
Предлагаю подробно рассмотреть некоторые её части.
Цикл - это разновидность управляющей конструкции в языках программирования, предназначенная для организации многократного 8 исполнения набора инструкций (операторов). Также циклом может называться любая многократно исполняемая последовательность инструкций, организованная любым способом [3].
Если в программе возникает необходимость неоднократно выполнить некоторые операторы, то используются операторы повтора (цикла).
Операторами цикла называются операторы, предназначенные для многократного выполнения определенной последовательности команд. У них всегда есть заголовок цикла, задающий число повторений, и тело цикла - набор повторяемых операторов [3].
В нашей программе мы будем использовать оператор цикла (for).
Оператор цикла FOR имеет такую структуру:
for переменная-счетчик: = начальное значение to конечное значение do повторяемые операторы;
for, to, do - являются зарезервированными словами (по-русски - для, до, выполнить).
Первоначально, до выполнения цикла значение счетчика берется равным "начальное значение". "Конечное значение" - определяет значение счетчика при котором тело цикла будет выполнено в последний раз.
Условие, управляющее работой оператора for, проверяется перед выполнением тела цикла и если условие не выполняется в самом начале, то "повторяемые операторы" не выполнятся ни разу [6].
Выполнив очередной раз тело цикла счетчик увеличивает свое значение на единицу. Затем происходит проверка, если счетчик не превышает конечного значения, то цикл вычислений повторяется, в противном случае работа оператора цикла завершается. Если у нас в начальном или конечном значении находятся вычисляемые выражения, то вычисление происходит однократно при первом проходе [3].
|
|
|
Условный оператор
С помощью условного оператора происходит проверка заданного условия и в зависимости от полученного результата происходит выбор одного из двух действий. Условный оператор представляет собой средство ветвления алгоритмического процесса.
Структура условного оператора представляет собой следующий вид:
if условие then список операторов 1 else список операторов 2;
где if, then, else - зарезервированные слова, по-русски означающие - если, то, иначе.
Условие выбора - это логическое выражение (в основном используются операторы сравнения) [3].
В данном случае, в нашей программе ELSE не будет использоваться, исходя из логики задачи.
Массивы
Массивом называется упорядоченная совокупность однотипных элементов, у которых общее имя. Массивы в языке Delphi во многом схожи с аналогичными типами данных в других языках программирования. В состав элементов массива могут входить данные любых типов, в том числе и структурированные. Любой элемент массива определяется именем массива и
индексом (индекс может быть не один, тогда данный массив будет многомерным). Количество индексов определяет размерность массива - одномерный, двумерный...[7].
Массивы бывают динамические и статические. Статический массив является таким массивом, размерность которого определена еще до компиляции программы. Описание статического типа будет в таком формате:
<Имя> = array [ <список инд.> ] of <тип>;
<Имя> - правильный идентификатор,of - зарезервированные слова (по русски - массив из), <список инд.> - список, состоящий из одного или нескольких индексных типов. Которые должны разделяться запятой и находиться в квадратных скобках.
<тип> - любой тип языка Delphi [3].
Динамический массив в составлении данной программы не нужен.
Переменные и их типы
При составлении программы важно помнить о ключевых, важных моментах без которых она не будет работать.
Мы разобрали часть основной составляющей нашей программы, а теперь нужно понять, что является обрамлением всех циклов, операторов и пр. Что объединяет их в единое.
Любая величина в Delphi может быть постоянной или переменной. Её имя (идентификатор) может состоять из комбинации латинских букв, цифр и знака подчёркивания, и начинаться не с цифры. При этом регистр символов значения не имеет.
Место описания данных в программе - вне логических блоков begin / end. В модуле перед ключевым словом implementation есть блок описания:Form1: TForm1; Именно здесь, начиная со следующей строки, удобно объявлять глобальные переменные и константы. Как видим, одна (Form1) уже есть [3]!
|
|
|
Команда объявления переменных в языке Delphi: var имя_переменной: тип_переменной; 11
Слово var - ключевое. Именем может быть любой идентификатор, если он не был описан ранее и не является одним из ключевых или зарезервированных слов языка Delphi. Если нужно описать несколько переменных одного типа, то их перечисляют, отделяя запятой: var A, B, C: Integer [7]; Если несколько описаний следуют друг за другом, то ключевое слово var повторно можно не указывать: var A, B: Integer; C, D: String [6];
Постоянную величину иначе называют константой. Но она встречаться в данной программе не будет.
Числа бывают целые и дробные. Наиболее удобным для использования в программах является тип Delphi Integer.
Дробные числа имеют дробную часть, отделяемую десятичной точкой. Наиболее удобным для использования в программах является тип Delphi Real.
|
|
|
