 |
Типовой расчет № 1 «Пространства и операторы»
|
|
|
|
И.В.Блинова, И.Ю. Попов, Е.С.Трифанова
ТИПОВЫЕ РАСЧЕТЫ
По функциональному анализу
Санкт-Петербург
Блинова И.В., Попов И.Ю., Трифанова Е.С. Типовые расчеты по функциональному анализу. – СПб: СПбГУ ИТМО, 2011. – 24 с.
Методическое пособие содержит два типовых расчета по функциональному анализу. Предназначено для студентов третьего курса ЕНФ и ИТиП, обучающихся по направлению 01.04.00 (Прикладная математика и информатика).
Рекомендовано к печати Советом естественнонаучного факультета СПбГУ ИТМО 01.03.2011 (протокол № 2)
В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория « Национальный исследовательский университет ». Министерством образования и науки Российской Федерации была утверждена Программа развития государственного образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный университет информационных технологий, механики и оптики» на 2009–2018 годы.
Ó Санкт-Петербургский государственный университет информационных технологий, механики и оптики, 2011
Ó Блинова И.В., Попов И.Ю., ТрифановаЕ.С., 2011
Типовой расчет № 1 «Пространства и операторы»
I. Проверить, образует ли 
метрическое пространство, если
.
Решение. Для того чтобы определить, является ли данное пространство метрическим, нужно проверить, удовлетворяет ли заданная функция расстояния 
, где 
трем аксиомам:
1) 
: 
, и 
;
2) : 
(аксиома симметрии);
3) 
: 
(аксиома треугольника).
Для данной функции выполнение условий 1) и 2) очевидно. Докажем выполнение аксиомы треугольника, которая примет вид
|
|
|
. (1)
Введем обозначения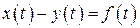 
, 
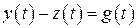. Тогда неравенство (1) примет вид
. (2)
Полученное неравенство следует из неравенства Коши-Буняковского:
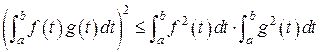. (3)
Имеем
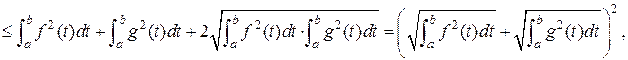
что равносильно неравенству (2). Следовательно, все три аксиомы выполнены, и данное пространство является метрическим.
II. Проверить, можно ли ввести норму в пространстве 
, 
следующим образом: 
.
Решение. Для того чтобы определить, может ли заданная функция 
являться нормой в пространстве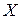 
, нужно проверить, удовлетворяет ли она трем условиям:
1) 
: 
, причем 
;
2) : 
;
3) 
: 
.
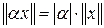Для данной функции выполнение условия 1) очевидно. Проверим выполнение условия 2). Воспользуемся свойствами модуля и супремума:
, .
Условие 3) также выполнено:
, .
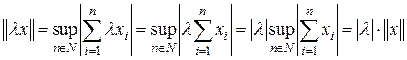Следовательно, функция 
задает норму на пространстве .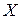
III. В пространстве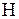 
найти проекцию элемента 
на подпространство, порожденное 
, если 
Решение. Обозначим 
- подпространство, порожденное функциями 
. Тогда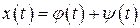 
, где 
- проекция на , 
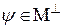. Разложим функцию 
по базису :
и найдем коэффициенты разложения 
и 
в этом базисе. Имеем
.
Умножим это равенство скалярно сначала на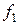 
, а затем на 
:
(4)
Вычислим скалярные произведения, зная, что 
. Имеем
, 
,
, 
, 
.
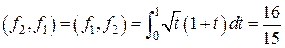Для решения системы (4) воспользуемся формулами Крамера. Определители системы
, 
, 
.
Тогда
, 
.
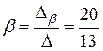И окончательно, 
.
IV. Показать, что оператор 
: 
, ограничен в пространстве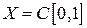 
, и найти его норму.
Решение. Докажем ограниченность оператора . В пространстве 
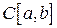норма элемента равна 
. Имеем
при 
. Следовательно, оператор ограничен.
Норма оператора определяется следующим образом: 
. Tогда получаем
V. Найти точечный спектр и собственные функции оператора A: 
, заданного на дважды непрерывно дифференцируемых функциях с граничными условиями 
в пространстве 
.
Решение. Запишем уравнение для определения собственных значений и собственных функций:
,
то есть
. (5)
Его решения будут разными в зависимости от знака выражения 
. Рассмотрим 3 случая:
|
|
|
1) 
. Тогда решение уравнения (5) имеет вид
.
Удовлетворим граничным условиям:
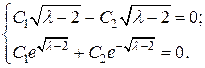
Отсюда следует, что 
, то есть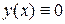 
, что противоречит определению собственной функции.
2) 
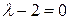. Решение уравнения (5) в этом случае имеет вид 
, и краевым условиям удовлетворяет только нулевая функция.
3) 
. Решение уравнения (5) имеет вид
.
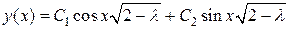Подставляя краевые условия, получим 
и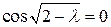 
. Находим спектр
, 
.
Соответствующие собственные функции (принадлежащие ) имеют вид
.
VI. Проверить, является ли оператор двукратного дифференцирования 
, определенный в комплексном пространстве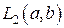 
на дважды непрерывно дифференцируемых функциях 
, удовлетворяющих граничным условиям 
, симметричным. Каким граничным условиям удовлетворяют функции из области определения сопряженного оператора?
Решение. Оператор называется симметричным, если выполняется условие
. (6)
Возьмем 
. Тогда
. Следовательно, для симметричности оператора необходимо и достаточно выполнения условия
,
то есть
. (7)
Так как 
, то функции 
удовлетворяют заданным граничным условиям. Подставим их в (7):
.
Полученное верное равенство равносильно симметричности оператора .
Пусть 
- оператор, сопряженный с . Он определяется так. 
, если существует элемент (обозначим его 
) такой, что (сравните с условием (6)):
.
Это условие аналогично условию (7), но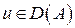 
, а . Подставим в (6) условия на функцию :
.
Поскольку 
и 
произвольны, получаем граничные условия на функцию : 
, откуда следует, что граничные условия для элемента из области определения 
те же, что и для оператора .
|
|
|
