Главная | Обратная связь | Поможем написать вашу работу!

Постоянный электрический ток

1. Закон Кулона

где и – величины точечных зарядов, – электрическая постоянная, – диэлектрическая проницаемость среды, r – расстояние между зарядами.

2. Напряженность электрического поля:

3. Напряженность поля

а) точечного заряда

;

б) бесконечно длиной заряженной нити

;

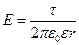в) равномерно зараженной бесконечной плоскости

;

где 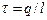– линейная плотность зарядов, – поверхностная плотность зарядов, r – расстояние до источника поля.

4. Работа перемещения заряда в электрическом поле

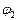где и - потенциалы начальной и конечной точек.

5. Потенциал поля точечного заряда

6. Связь между потенциалом и напряженность

7. Электроемкость

где φ – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U – разность потенциалов пластин конденсаторов.

8. Электроемкость плоского конденсатора

где S – площадь пластины (одной) конденсатора, d – расстояние между пластинами.

9. Электроемкость батареи конденсаторов

а) при последовательном соединении

;

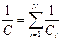б) при параллельном соединении

где N – число конденсаторов в батарее.

10. Энергия поля

а) заряженного проводника

;

б) заряженного конденсатора

11. Сила тока

12. Сила постоянного тока

где q – заряд, прошедший через поперечное соединение проводника за время t.

13. Плотность тока

где S – поперечное сечение проводника.

Связь плотности тока со средней скоростью направленного движения заряженных частиц.

где n – концентрация заряженных частиц.

14. Закон Ома

а) для участка цепи, не содержащего ЭДС

где – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка.

б) для участка цепи, содержащего ЭДС

где – ЭДС источника, R – полное сопротивление участка (сумма внешних и внутренних сопротивлений).

15. Сопротивление

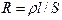где 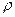- удельное сопротивление, l – длина проводника, S – площадь поперечного сечения проводника.

16. Сопротивление системы проводников

а) при последовательном соединении

;

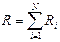б) при параллельном соединении

17. Зависимость удельного сопротивления от температуры

где - температурный коэффициент сопротивления, t – температура по шкале Цельсия.

18. Работа тока

, , ,

Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка не содержащего ЭДС.

19. Мощность тока

, , .

20. Закон Джоуля-Ленца

КОНТРОЛЬНАЯ РАБОТА №1

1. Определить среднюю скорость тела, участвующего в двух последовательных и одинаковых по величине перемещениях: сначала со скоростью 15 км/ч, а потом со скоростью 25 км/ч.

2. Два тела движутся со скоростями 27 км/ч и 19 км/ч под углом 60º друг к другу. Найти скорость первого тела относительно второго.

3. Когда пассажиру оставалось дойти до двери своего вагона 15 м, поезд тронулся с места и начал двигаться с ускорением 0,5 м/с. Через сколько времени пассажир достигнет двери вагона?

4. Тело брошено вертикально вверх с начальной скоростью 4 м/с. Когда оно достигло высшей точки траектории, из той точки, из которой оно было брошено, с той же начальной скоростью было брошено второе тело. На каком расстоянии от начальной точки тела встретятся?

5. С башни высотой 49 м в горизонтальном направлении брошено тело со скоростью 5 м/с. На каком расстоянии от башни оно упало и какова его скорость в момент удара о землю?

6. Точка движется согласно уравнениям х = 7 + 4t и y = 2 + 3t (в единицах СИ). Какова скорость движения точки?

7. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением s = 100 + 10t – 0,5t². Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения в конце пятой секунды.

8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением s = t³ + 4t² – t + 8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала движения.

9. Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t³. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

10. Тело вращается равноускоренно с начальной угловой скоростью 5 с^-1 и угловым ускорением 1 с^-2. Сколько оборотов сделает тело за 10 с?

11. Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону
x = 10 + 5t – 10t²? Масса тела 2 кг.

12. Найти закон движения тела массой 1 кг под действием постоянной силы 10 Н, если в момент t = 0 тело покоилось в начале координат
(x = 0).

13. Найти закон движения тела массой 1 кг под действием постоянной силы 2 Н, если в момент t = 0 имеем x = 0 и v₀ = 2 м/с.

14. Тело массой 2 кг движется с ускорением, изменяющимся по закону
a = 5t – 10. Определите силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.

15. Материальная точка массой 1 кг движется под действием некоторой силы согласно уравнению х = 3 + 8t + t² – 0,2t³. Найти значение этой силы через 2 и 5 с после начала движения. В какой момент времени сила равна нулю?

16. С какой силой нужно действовать на тело массой 2 кг, чтобы оно поднималось вертикально вверх с ускорением, вдвое большим ускорения свободного падения?

17. Космонавт массой 60 кг при вертикальном взлете ракеты давит на опору с силой 5400 Н. Найти ускорение ракеты.

18. На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить к грузу, чтобы втаскивать его: а) с постоянной скоростью;
б) с ускорением 1 м/с²? Коэффициент трения 0,2.

19. Два тела массами 300 и 200 г связаны нитью и расположены на гладкой горизонтальной поверхности. С какой максимальной силой, направленной горизонтально, нужно тянуть первое тело, чтобы нить, способная выдержать нагрузку 6 Н, не оборвалась?

20. На концах нити, перекинутой через невесомый блок с неподвижной осью, подвешены тела массами по 0,49 кг каждое. Какова масса дополнительного груза, который надо положить на одно из тел, чтобы каждое из них прошло за 4 с путь 1,6 м?

21. Сплошной шар массой 1 кг и радиусом 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением φ = 10 + 5t – 2t². В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.

22. Сплошной цилиндр массой 0,1 кг катится без скольжения со скоростью 4 м/с. Определить кинетическую энергию цилиндра и время для его остановки, если на цилиндр подействует сила трения 0,1 Н.

23. Сплошной шар скатывается по наклонной плоскости, длина которой 1 м и угол наклона 30˚. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.

24. Полый цилиндр массой 1 кг катится по горизонтальной поверхности со скоростью 10 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 2 м.

25. Маховик, имеющий форму диска массой 10 кг и радиуса 0,1 м, был раскручен до частоты 120 мин^-1.Под действием силы трения маховик остановился через 10 с. Найти момент силы трения, считая его постоянным.

26. По касательной к шкиву маховика в виде диска диаметром 75 см и массой 40 кг приложена сила 1 кН. Определить угловое ускорение и частоту вращения маховика через 10 с после начала действия силы, если радиус шкива равен 12 см. Силой трения пренебречь.

27. По горизонтальной плоскости катится диск со скоростью 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь 18 м.

28. Маховик, массу которого можно считать распределенной по ободу радиуса 18 см, вращается со скоростью, соответствующей
600 об/мин. Под действием тормозящего момента 10 Н·м маховик останавливается. Найти, через сколько времени он остановился, какое число оборотов совершил за это время и какова работа торможения.

29. По наклонной плоскости вверх катится без скольжения обруч. Ему сообщена начальная скорость 3,14 м/с, параллельная наклонной плоскости. Найти путь, пройденный обручем до остановки, если угол наклона плоскости 30°.

30. Однородный стержень массой 0,3 кг и длиной 1,2 м вращается вокруг вертикальной оси, проходящей через один из концов стержня. Чему равен вращающий момент, если угловое ускорение стержня 98,1 с^-2? Как изменится вращающий момент, если ось вращения переместить в центр стержня?

31. По небольшому куску мягкого железа, лежащему на наковальне массой 300 кг, ударяет молот массой 8 кг. Определить КПД удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

32. С покоящимся шаром массой 2 кг сталкивается такой же шар, движущийся со скоростью 1 м/с. Вычислить работу деформации при прямом центральном неупругом ударе.

33. Масса снаряда 10 кг, масса ствола орудия 500 кг. При выстреле снаряд получает кинетическую энергию 1,5·10⁶ Дж. Какую кинетическую энергию получает ствол орудия при отдаче?

34. Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 2 кг со скоростью 10 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед 0,02?

35. Тело массой 2 кг, движущееся со скоростью 10 м/с, сталкивается с неподвижным телом массой 3 кг. Считая удар центральным и неупругим, найти количество теплоты, выделившееся при ударе.

36. Человек массой 70 кг, бегущий со скоростью 9 км/ч, догоняет тележку массой 190 кг, движущуюся со скоростью 3,6 км/ч, и вскакивает на нее. С какой скоростью начнет двигаться тележка? С какой скоростью начнет двигаться тележка с человеком, если человек бежал навстречу тележке?

37. Молекула водорода, Двигающаяся со скоростью 400 м/с, подлетает к стенке сосуда под углом 60° и упруго ударяется о нее. Определить импульс, полученный стенкой. Принять массу молекулы равной
3·10^-27 кг.

38. В деревянный шар массой 8 кг, подвешенный на нити длиной 1,8 м, попадает горизонтально летящая пуля массой 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

39. Конькобежец, стоя на коньках на льду, бросает камень массой 2,5 кг под углом 30° к горизонту со скоростью 10 м/с. Какова начальная скорость движения конькобежца, если его масса 60 кг? На какое расстояние он откатится, если коэффициент трения коньков о лед 0,04?

40. Стальной шарик массой 50 г упал с высоты 1 м на большую плиту, передав ей импульс силы, равный 0, 27 Н·с. Определить количество теплоты, выделившееся при ударе и высоту, на которую поднимется шарик.

41. Материальная точка массой 7,1 г совершает гармонические колебания с амплитудой 2 см и частотой 5 Гц. Определить максимальную возвращающую силу и полную энергию колебаний.

42. Максимальное значение скорости материальной точки 8 см/с, а максимальное значение ускорения 16 см/с². Найти амплитуду смещения и циклическую частоту колебаний.

43. Период колебаний математического маятника 10 с. Длина этого маятника равна сумме длин двух других математических маятников, один из которых имеет частоту 1/6 Гц. Чему равен период колебаний второго маятника?

44. Физический маятник представляет собой тонкий стержень, подвешенный за один из его концов. При какой длине стержня период колебаний этого маятника будет равен 1 с?

45. Однородный диск радиусом 40 см колеблется в вертикальной плоскости около горизонтальной оси. Ось перпендикулярна диску и проходит через его край. Как изменится период колебаний диска, если ось перенести к центру параллельно самой себе на расстояние ¼ радиуса?

46. На пружине подвешено тело массой 2 кг. Найти коэффициент упругости пружины, если тело колеблется с частотой 6 Гц.

47. Точка совершает гармонические колебания, уравнение которых
х = А sinωt, где А = 5 см, ω = 2 с^-1. В момент времени, когда точка обладала потенциальной энергией 0,1 мДж, на нее действовала сила
5 мН. Найти этот момент времени.

48. Определить частоту гармонических колебаний диска радиусом 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

49. Определить смещение, скорость и ускорение колеблющейся точки через 1/24 с после начала движения. Уравнение гармонического колебания имеет вид: х = 10sin4πt (см).

50. Тонкий обруч, повещенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча 30 см. Вычислить период колебаний обруча.

51. Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0,20 г водорода при температуре 27° С.

52. Давление одноатомного идеального газа 10 мПа, концентрация молекул 2·10¹² см ^–3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.

53. Определить среднее значение полной кинетической энергии одной молекулы аргона и водяного пара при температуре 300 К.

54. Определить давление которое оказывает азот на стенки сосуда, если концентрация молекул 2,7·10¹⁹ см^-3, а их средняя квадратичная скорость 400 м/с.

55. Определить полную кинетическую энергию молекул азота, который находится в баллоне объемом 100 л при давлении 1,5·10⁵ Па.

56. В сосуде, имеющем форму шара радиуса 0,1 м, находится 5,6 г азота. До какой температуры можно нагреть сосуд, если его стенки выдерживают давление 5·10⁵ Па?

57. Вычислить плотность азота, находящегося в баллоне под давлением
2 МПа и имеющего температуру 400 К.

58. Два сосуда одинакового объема содержат кислород. В одном сосуде давление 2 МПа и температура 800 К, а в другом давление2,5 МПа и температура 200 К. Сосуды соединили трубкой и охладили содержащийся в них газ до температуры 200 К. Определить установившееся в сосудах давление.

59. В сосуде вместимостью 40 л находится кислород при температуре 27° С. Когда часть газа израсходовали, давление в баллоне понизилось на 100 кПа. Определить массу израсходованного кислорода. Температура газа оставалась неизменной.

60. 0,4 кг аргона содержится в сосуде под давлением 4 атм. Какую массу аргона следует добавить в сосуд, чтобы давление увеличилось на
3 атм? Температуру считать постоянной.

61. Какое количество теплоты необходимо сообщить аргону массой
400 г, чтобы нагреть его на 100 К: а) при постоянном объеме;
б) при постоянном давлении.

62. Во сколько раз увеличится объем 2 молей кислорода при изотермическом расширении при температуре 300 К, если при этом газу сообщили 4 кДж теплоты?

63. Какое количество теплоты нужно сообщить 2 молям кислорода чтобы он совершил работу в 1000 Дж: а) при изотермическом процессе; б) при изобарном процессе?

64. Найти работу, которую совершит азот, если ему при постоянном давлении сообщить 21 кДж теплоты. Найти также изменение внутренней энергии газа.

65. Определить количество теплоты, сообщенное 88 г углекислого газа, если он был изобарно нагрет от 300 до 350 К. Какую работу совершает при этом газ и как изменится его внутренняя энергия?

66. Какое количество теплоты надо сообщить кислороду объемом 50 л при его изохорном нагревании, чтобы давление газа повысилось на 0,5 МПа?

67. При изотермическом расширении 200 г азота при температуре 7° С его объем увеличился в два раза. Определить совершенную при этом работу, изменение внутренней энергии газа и количество теплоты, полученное газом.

68. Азот, занимавший объем 10 л под давлением 0,2 МПа, изотермически расширился до объема 28 л. Определить работу расширения, изменение внутренней энергии и количество сообщенной газу теплоты.

69. Водород массой 10 г нагрели на 200 К, причем газу было передано
40 кДж теплоты. Найти изменение внутренней энергии водорода и совершенную им работу.

70. При изохорном нагревании кислорода объемом 50 л давление газа изменилось на 0,5 МПа. Найти количество теплоты, сообщенное газу.

71. В вершинах квадрата со стороной 10 см расположены равные одноименные заряды. Потенциал создаваемого ими в центре квадрата поля равен 500 В. Определить заряд в вершине квадрата.

72. В вершинах квадрата со стороной 50 см расположены заряды одинаковой величины. В случае, когда два соседних заряда положительные, а два других – отрицательные, напряженность поля в центре квадрата равна 144 В/м. Определить величину заряда в вершине квадрата.

73. В вершинах квадрата со стороной 10 см расположены заряды по
0,1 нКл. Определить напряженность и потенциал поля в центре квадрата, если один из зарядов отличается по знаку от остальных.

74. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 0,1 нКл. Определить напряженность и потенциал поля в точке, находящейся на расстоянии 5 см от каждого из зарядов.

75. Заряды по 0,1 нКл расположены в вершинах равностороннего треугольника со стороной 20 см. Результирующая сила, действующая на четвертый заряд, помещенный в середину одной из сторон треугольника, равна 0,6 мкН. Определить величину этого заряда и потенциал поля в точке его расположения.

76. На расстоянии 6 см друг от друга находятся два точечных заряда +0,8 мкКл и – 0,4 мкКл. Найти напряженность и потенциал поля в точке, отстоящей от положительного заряда на расстоянии 5 см и от отрицательного заряда на расстоянии 4 см.

77. Точечные заряды – 0,02 мкКл и +0,04 мкКл расположены на таком расстоянии, при котором сила взаимодействия между ними равна 2мН. С какой силой действуют эти заряды на третий +0,1 мкКл, находящийся за вторым зарядом на расстоянии 3 см? Все заряды расположены на одной прямой.

78. Четыре одинаковых заряда пол 40 нКл расположены в вершинах квадрата со стороной 10 см. Найти силу, действующую на один из зарядов со стороны трех остальных.

79. Точечные заряды 30 мкКл и – 20 мкКл находятся на расстоянии 20 см друг от друга. Определить напряженность электрического поля в точке, удаленной от первого заряда на расстояние 30 см, а от второго – на расстояние 15 см.

80. В двух вершинах правильного треугольника со стороной 10 см находятся заряды 10 мкКл и 20 мкКл. Определить напряженность поля в третьей вершине треугольника.

81. В поле бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда 10 мкКл/м² перемещается заряд из точки, расположенной на расстоянии 10 см от плоскости, в точку на расстоянии 50 см от нее. Определить величину заряда, если при этом совершается работа 1 мДж.

82. Заряд 1 нКл переносится из бесконечности в точку, находящуюся на расстоянии 10 см от поверхности сферы диаметром 10 см, заряженной с поверхностной плотностью 10^-3 Кл/м². Определить работу перемещения заряда.

83. Заряд – 1 нКл переместился в поле заряда +1,5 нКл из точки с потенциалом 100 В в точку с потенциалом 600 В. Определить работу сил поля и расстояние между этими точками.

84. Заряд 1 нКл находится на расстоянии 20 см от бесконечно длинной равномерно заряженной нити. Под действием сил поля заряд перемещается на расстояние 0,1 м. Определить линейную плотность заряда нити, если работа сил поля равна 0,1 мкДж.

85. Заряд 10 нКл создает электрическое поле. Какую работу совершают силы этого поля при перемещении заряда 1 нКл вдоль силовой линии из точки, находящейся на расстоянии 8 см от первого заряда, до расстояния 1 м от него?

86. Конденсатор с парафиновым диэлектриком заряжен до разности потенциалов 150 В. Напряженность поля 6·10⁶ В/м, площадь пластин 6 см². Определить емкость конденсатора и поверхностную плотность заряда на обкладках.

87. Вычислить емкость батареи, состоящей из трех конденсаторов емкостью 1 мкФ каждый, при всех возможных видах их соединения.

88. Конденсатор емкостью 6 мкФ, соединенный последовательно с конденсатором неизвестной емкости, подключен к источнику постоянного напряжения 12 В. Определить емкость второго конденсатора и напряжения на каждом из них, если заряд батареи 24 мкКл.

89. Площадь пластин плоского слюдяного конденсатора 1,1 см², зазор между ними 3 мм. При разряде конденсатора выделилась энергия
1 мкДж. До какой разности потенциалов был заряжен конденсатор?

90. Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1см². Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.

91. Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м². Определить разность потенциалов на концах проводника.

92. Определить плотность тока, текущего по проводнику длиной 5 м, если на концах его поддерживается разность потенциалов 2 В. Удельное сопротивление материала 2 мкОм·м.

93. Напряжение на концах проводника сопротивлением 5 Ом за 0,5 с равномерно возрастает от 0 до 20 В. Какой заряд проходит через проводник за это время?

94. Температура вольфрамовой нити электролампы 2000 ºС, диаметр
0,02 мм, сила тока в ней 4 А. Определить напряженность поля в нити.

95. На концах никелинового проводника длиной 5 м поддерживается разность потенциалов 12 В. Определить плотность тока в проводнике, если его температура 540 ºС.

96. Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 2 А его КПД равен 0,8. Определить ЭДС аккумулятора.

97. Определить ЭДС аккумуляторной батареи, ток короткого замыкания которой 10 А, если при подключении к ней резистора сопротивлением 0,2 Ом сила тока в цепи равна 1 А.

98. К источнику тока подключают один раз проводник сопротивлением
1 Ом, другой раз – сопротивлением 4 Ом. В обоих случаях за одно и то же время на проводнике выделяется одинаковое количество теплоты. Определить внутреннее сопротивление источника тока.

99. Два проводника сопротивлениями 7 и 5 Ом соединены параллельно и подключены к источнику тока. В первом проводнике выделилось
300 Дж теплоты. Какое количество теплоты выделится во втором проводнике за то же время?

100.Две одинаковые электролампы включены в сеть постоянного напряжения 20 В один раз последовательно, другой раз параллельно. Во втором случае потребляемая лампами мощность на 6 Вт больше, чем в первом. Найти сопротивление каждой лампы, считая его постоянным.

ЭЛЕКТРОМАГНЕТИЗМ

1. Связь магнитной индукции В с напряженностью Н магнитного поля

где 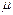– магнитная проницаемость изотропной среды, - магнитная постоянная. В вакууме .

2. Закон Био-Савара-Лапласа

или ,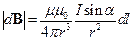

где d B – магнитная индукция поля, создаваемого элементом провода длиной dl с током I, r – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция, - угол между радиусом-вектором и направлением тока в элементе провода.

3. Магнитная индукция в центре кругового тока

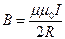где R – радиус кругового витка.

4. Магнитная индукция на оси кругового тока

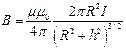где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

5. Магнитная индукция поля прямого тока

где R – радиус кругового витка.

6. Магнитная индукция поля прямого тока

где – расстояние от оси провода до точки, в которой определяется индукция.

7. Магнитная индукция поля, создаваемого отрезком провода с током,

8. Сила Лоренца

или ,

где v – скорость заряженной частицы, q – заряд частицы, 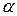– угол между векторами v и B.

9. Магнитный поток

а) в случае однородного магнитного поля и плоской поверхности

или ,

где S – площадь контура, – угол между нормалью к плоскости контура и вектором магнитной индукции.

б) в случае неоднородного поля и произвольной поверхности

(интегрирование ведется по всей поверхности).

10. Потокосцепление (полный поток)

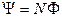Это формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

11. Работа по перемещению замкнутого контура в магнитном поле

12. ЭДС индукции

13. Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур

или ,

где R – сопротивление контура.

14. Индуктивность контура

15. ЭДС самоиндукции

16. Индуктивность соленоида

где n – отношение числа витков соленоида к его длине, V – объем соленоида.

ОПТИКА

1. Скорость света в среде

где с – скорость света в вакууме, n – показатель преломления среды.

2. Оптическая длина пути световой волны

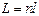где l – геометрическая длина пути световой волны в среде с показателем преломления n.

3. Оптическая разность хода двух световых волн

4. Зависимость разности фаз от оптической разности хода световых волн

где – длина световой волны.

5. Условие максимального усиления света при интерференции

, (k =0, 1, 2, …).

6. Условие максимального ослабления света при интерференции

7. Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки

или

где d – толщина пленки, n – показатель преломления пленки, i ₁ – угол падения, i ₂ – угол преломления света в пленке.

8. Угол отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия

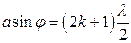, (k =0, 1, 2, …),

где а – ширина щели, k – порядковый номер максимума.

9. Угол отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции света на дифракционной решетке, определяется из условия

, (k =0, 1, 2, …),

где d – период дифракционной решетки.

10. Закон Брюстера

где – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован, n ₂₁ – относительный показатель преломления второй среды относительно первой.

11. Закон Малюса

где I ₀ – интенсивность плоскополяризованного света, падающего на анализатор, I – интенсивность этого света после анализатора, 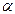– угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).

12. Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество

а) в твердых телах

где – постоянная вращения, d – длина пути, пройденного светом в оптически активном веществе.

б) в растворах

где – удельное вращение, – массовая концентрация оптически активного вещества в растворе.

13. Закон Стефана-Больцмана

где – энергетическая светимость (излучательность) абсолютно черного тела, 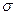– постоянная Стефана-Больцмана, Т – термодинамическая температура Кельвина.

14. Закон смещения Вина

где – длина волны, на которую приходится максимум энергии излучения, b – постоянная Вина в законе смещения.

15. II закон Вина

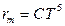где – максимальная испускательная способность абсолютно черного тела, С – постоянная Вина.

16. Формула Эйнштейна для фотоэффекта

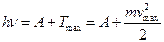где – энергия фотона, падающего на поверхность металла, А – работа выхода электрона, – максимальная кинетическая энергия фотоэлектрона.

17. Красная граница фотоэффекта

или ,

где 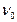– минимальная частота света, при которой еще возможен фотоэффект, – максимальная длина волны, при которой еще возможен фотоэффект, h – постоянная Планка, с – скорость света в вакууме.

18. Давление света при нормальном падении на поверхность

где – энергетическая освещенность (облученность), w – объемная плотность энергии излучения, – коэффициент отражения.

ЭЛЕМЕНТЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ

1. Момент импульса электрона (второй постулат Бора)

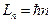или ,

где m – масса электрона, – скорость электрона на n -ой орбите, – радиус n -ой стационарной орбиты, 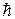– постоянная Планка, n – главное квантовое число (n =1, 2, 3, …).