 |
п.5.1. Геометрическое приложение определенного интеграла.
|
|
|
|
Тема 5. Геометрический смысл определенного интеграла.


(см. Рис. 1.)
Рис. 1

(см. Рис. 2)

Рис. 2.

(см. Рис. 3.)

Рис. 3.
п.5.1. Геометрическое приложение определенного интеграла.

1) Вычисление площади криволинейной трапеции
1) Пусть функция 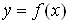 неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке 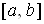 . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью
. Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью  , слева и справа – прямыми
, слева и справа – прямыми  и
и  (см. рис. 1) вычисляется по формуле
(см. рис. 1) вычисляется по формуле
 . (1)
. (1)
Пример. Найти площадь фигуры, ограниченной линией  и осью
и осью  .
.

Рис. 6
Решение. Графиком функции  является парабола, ветви которой направлены вниз. Построим ее (рис. 6). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью
является парабола, ветви которой направлены вниз. Построим ее (рис. 6). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью  (прямой
(прямой  ). Для этого решаем систему уравнений
). Для этого решаем систему уравнений
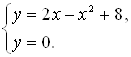
Получаем:  , откуда
, откуда  ,
, 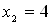 ; следовательно,
; следовательно,  ,
,  .
.
Площадь фигуры находим по формуле (1):
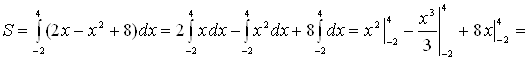

 (кв. ед.).
(кв. ед.).
2) Если функция  неположительна и непрерывна на отрезке
неположительна и непрерывна на отрезке  , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью
, то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью  , слева и справа – прямыми
, слева и справа – прямыми  и
и  , вычисляется по формуле
, вычисляется по формуле
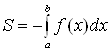 . (2)
. (2)
3) В случае если функция 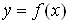 непрерывна на отрезке
непрерывна на отрезке 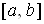 и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 7) равна алгебраической сумме соответствующих определенных интегралов:
и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 7) равна алгебраической сумме соответствующих определенных интегралов:

Рис. 7
 . (3)
. (3)
Пример. Вычислить площадь фигуры, ограниченной осью  и графиком функции
и графиком функции 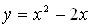 при
при  .
.

Рис. 8
Решение. Сделаем чертеж (рис. 8). Искомая площадь представляет собой сумму площадей  и
и  . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему
. Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему  Получим
Получим  ,
,  . Следовательно:
. Следовательно:
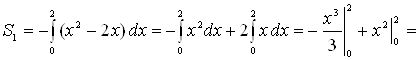
 ;
;

 .
.
Таким образом, площадь  заштрихованной фигуры равна
заштрихованной фигуры равна
|
|
|
 (кв. ед.).
(кв. ед.).
4) Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке 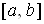 функций
функций  и
и 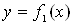 ,
,
а слева и справа – прямыми  и
и  (рис. 9).
(рис. 9).

Рис. 9
Тогда ее площадь вычисляется по формуле
 . (4)
. (4)
Пример. Найти площадь фигуры, ограниченной линиями  и
и 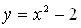 .
.

Рис. 10
Решение. Данная фигура изображена на рис. 10. Площадь ее вычислим по формуле (4). Решая систему уравнений  находим
находим  ,
,  ; следовательно,
; следовательно,  ,
,  . На отрезке
. На отрезке  имеем:
имеем:  . Значит, в формуле (4) в качестве
. Значит, в формуле (4) в качестве  возьмем x, а в качестве
возьмем x, а в качестве  –
–  . Получим:
. Получим:


 (кв. ед.).
(кв. ед.).
5) Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
Пример. Найти площадь фигуры, ограниченной линиями  ,
, 
 ,
,  .
.

Рис. 11
Решение. Сделаем чертеж (рис. 11). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью  , слева и справа – прямыми
, слева и справа – прямыми  и
и  , сверху – графиками функций
, сверху – графиками функций  и
и  . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой
. Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой  на две части (1 – это абсцисса точки пересечения линий
на две части (1 – это абсцисса точки пересечения линий  и
и  ). Площадь каждой из этих частей находим по формуле (1):
). Площадь каждой из этих частей находим по формуле (1):
 (кв.ед.);
(кв.ед.); 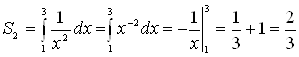 (кв. ед.).
(кв. ед.).
Следовательно:
 (кв. ед.).
(кв. ед.).
6) В заключение отметим, что если криволинейная трапеция ограничена прямыми  и
и 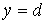 , осью
, осью  и непрерывной на
и непрерывной на  кривой
кривой  (рис. 12),
(рис. 12),

Рис. 12
то ее площадь находится по формуле 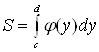 .
.
Примеры.



2) Несобственные интегралы с бесконечными пределами интегрирования.
При введении понятия определённого интеграла  предполагалось, что выполняются следующие два условия:
предполагалось, что выполняются следующие два условия:
а) пределы интегрирования a и b являются конечными;
б) подынтегральная функция  ограничена на отрезке
ограничена на отрезке 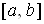 .
.
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
|
|
|
Определение. Пусть функция 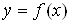 определена и непрерывна на промежутке
определена и непрерывна на промежутке  , тогда
, тогда
 (8)
(8)
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если  существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл  называется сходящимся; если данный предел не существует или равен
называется сходящимся; если данный предел не существует или равен  , то несобственный интеграл называется расходящимся.
, то несобственный интеграл называется расходящимся.
!!! Геометрически несобственный интеграл  от неотрицательной функции
от неотрицательной функции  выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции
выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции 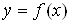 , снизу – осью
, снизу – осью  , слева – отрезком прямой
, слева – отрезком прямой  и неограниченной справа (рис. 18).
и неограниченной справа (рис. 18).
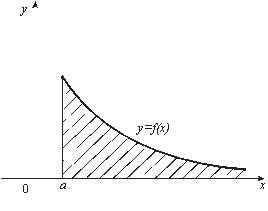
Рис. 18
(!!! Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна)
Определение. Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
 . (9)
. (9)
Этот интеграл сходится, если предел в правой части равенства (9) существует и конечен; в противном случае интеграл называется расходящимся.
Определение. Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
 (10)
(10)
где с – любая точка интервала  . Интеграл
. Интеграл  сходится только в том случае, когда сходятся оба интеграла в правой части равенства (10).
сходится только в том случае, когда сходятся оба интеграла в правой части равенства (10).
Пример. Исследовать на сходимость несобственные интегралы:
а)  ; б)
; б) 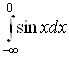 ; в)
; в)  ; г)
; г)  .
.
Решение. а) 
 , следовательно, данный интеграл расходится;
, следовательно, данный интеграл расходится;
б) 
 . Так как при
. Так как при  предел
предел  не существует, то интеграл
не существует, то интеграл  расходится;
расходится;
в) 
 Значит, несобственный интеграл
Значит, несобственный интеграл 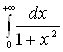 сходится и его значение равно
сходится и его значение равно  ;
;
г)  = [выделим в знаменателе полный квадрат:
= [выделим в знаменателе полный квадрат:  ] =
] = 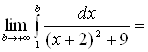 [замена:
[замена: 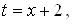
 ] =
] = 


Значит, несобственный интеграл сходится и его значение равно  .
.
3) Несобственные интегралы от неограниченных функций.
Пусть функция 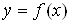 непрерывна на конечном промежутке
непрерывна на конечном промежутке  , но не ограничена на этом промежутке.
, но не ограничена на этом промежутке.
Определение. Несобственным интегралом  от функции у=f(x) на промежутке
от функции у=f(x) на промежутке  называется предел
называется предел  , т.е.
, т.е.
 . (11)
. (11)
Если предел, стоящий в правой части равенства (11) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Интеграл (11) иногда называют несобственным интегралом второго рода.
|
|
|
Определение. Аналогично вводится понятие несобственного интеграла от функции 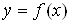 непрерывной, но не ограниченной на промежутке
непрерывной, но не ограниченной на промежутке  :
:
 . (12)
. (12)
Определение. Если функция 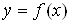 не ограничена при
не ограничена при  , где
, где  , и непрерывна при
, и непрерывна при 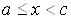 и
и  , то несобственный интеграл от функции у=f(x) на отрезке
, то несобственный интеграл от функции у=f(x) на отрезке  обозначается
обозначается  и определяется равенством
и определяется равенством
 . (13)
. (13)
Несобственный интеграл (13) называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства (13). В противном случае данный интеграл называется расходящимся.
Пример. Исследовать на сходимость несобственные интегралы:
а)  ; б)
; б)  .
.
Решение: а) данный интеграл является интегралом от неограниченной функции (подынтегральная функция  не определена в точке
не определена в точке  , при
, при  эта функция неограниченно возрастает).
эта функция неограниченно возрастает).
По определению имеем
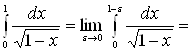 [замена:
[замена: 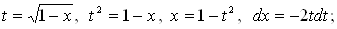
 ] =
] = 
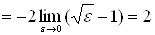 , следовательно, данный интеграл сходится.
, следовательно, данный интеграл сходится.
б) по определению


 .
.
Значит, данный интеграл является расходящимся.
|
|
|


