 |
Исследование устойчивости импульсных систем
|
|
|
|
Построение переходных процессов по передаточной функции
Импульсной системы
1 способ
Имеется передаточная функция замкнутой системы
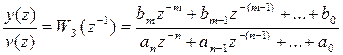 . (п. 4.1.)
. (п. 4.1.)
Исходя из (п.4.1) записываем алгебраическое выражение
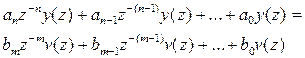 (п. 4.2.)
(п. 4.2.)
Подвергая выражение (п. 4.2.) обратному Z - преобразованию получим
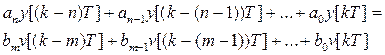 . (п. 4.3.)
. (п. 4.3.)
Путём подстановки в (п. 4.3.) значения тактов квантования k = 0, 1, 2 … получим значения выходной величины y[kT] в зависимости от задающего сигнала v[kT].
Пример:
 .
.
После обратного Z - преобразования получим
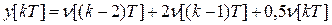 .
.
В частности, если задающий сигнал постоянный, например единичный сигнал, получим
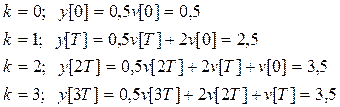
Следовательно, при k = 2 (на втором такте) переходный процесс выходит на установившийся режим. График решетчатой функции показан на рис. п. 5.1.
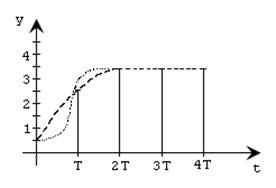
Рис. 4.1. Решетчатая функция переходного процесса y[kT] и возможные
варианты непрерывной (реальной) кривой переходного процесса
Вид непрерывных кривых переходных процессов для одной и той же решетчатой функции могут значительно отличаться. Это зависит от динамических свойств объекта управления.
2 способ
Из сравнения выражений дискретной функции
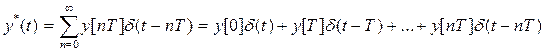 (п. 4.4)
(п. 4.4)
и ее z-изображение
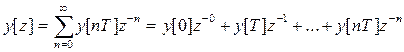 (п. 4.5)
(п. 4.5)
видно, что коэффициенты разложения (п.4.5) равны значениям решетчатой функции в соответствующие такты времени. Отсюда следует второй способ нахождения обратного z-преобразования.
Из передаточной функции (п. 4.1) следует, что
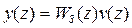
или записав выражение (п. 4.1) и выражение для v(z) относительно положительных степеней z в общем случае получим
 . (п. 4.6)
. (п. 4.6)
Разложим выражение y(z) в степенной ряд по отрицательным степеням z (в ряд Лорана) путем деления полинома числителя выражения (п. 4.6) на полином знаменателя:
|
|
|
 .
.
В соответствии с выражением (п. 4.5) получим, что
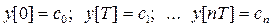 .
.
Пример
Возьмем ту же передаточную функцию, что и в примере построения переходных процессов первым способом.
Так как задающий (входной) сигнал единичный: v[kT] = 1[kT],
то 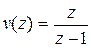 .
.
Следовательно,
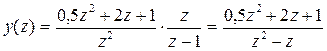 .
.
Разложим выражение для y(z) в ряд Лорана путем деления полинома числителя на полином знаменателя
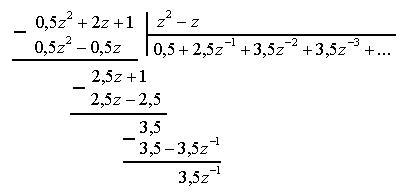
Таким образом
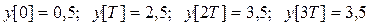 .
.
Т.е. получили, очевидно, тот же результат что и первым способом.
3 способ заключается в непосредственном применении обратного Z - преобразования:
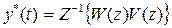 . (п. 4.7)
. (п. 4.7)
Осуществить обратное Z – преобразование наиболее просто путём использования таблиц этого преобразования. Если в фигурных скобках (п.4.7) стоит сложное (не табличное) выражение, то его необходимо разложить на простые слагаемые, чтобы непосредственно использовать таблицу прямого и обратного Z - преобразования функций.
Из приведенных примеров видно, что построение переходных процессов по импульсной передаточной функции значительно проще, чем пл непрерывным передаточным функциям. Это объясняется тем, что коэффициенты импульсных функций по существу представляют пошаговое решение дифференциальных уравнений, описывающих динамику замкнутой системы управления.
Приложение 5
Исследование устойчивости импульсных систем
Если известны передаточная функция замкнутой импульсной системы (п. 4.1), то устойчивость этой системы, как и в случае непрерывных систем, определяется по виду корней характеристического уравнения этой системы
 . (п. 5.1)
. (п. 5.1)
У устойчивой импульсной системы корни уравнения (п.5.1) по модулю меньше единицы 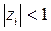
Если хоть один корень уравнения (п. 5.1) по модулю будет равен единице, то системы находится на границе устойчивости, а если 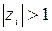 , то система будет неустойчива. Доказательство этого положения дано в параграфе 2.2. Графически условие устойчивости импульсной системы представлено на рис. п.5.1.
, то система будет неустойчива. Доказательство этого положения дано в параграфе 2.2. Графически условие устойчивости импульсной системы представлено на рис. п.5.1.
|
|
|

а) б)
Рис. п.5.1 Комплексные плоскости расположения корней характеристического уравнения импульсной системы^
а) Z - плоскость; б) w-плоскость
Как видно из рисунка п. 5.1.а, условием устойчивости импульсной системы является нахождение всех корней характеристического уравнения внутри единичного радиуса комплексной Z - плоскости.
Если применить билинейное преобразование переменной z в переменную w с помощью следующего соотношения
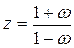 , (п. 5.2)
, (п. 5.2)
то единичная окружность в комплексной w-плоскости (рис. п.5.1.б) преобразуется в мнимую ось, а область, ограниченная этой окружностью - в левую полуплоскость. Поэтому, заменив в уравнении (п. 5.1) переменную z на переменную wс помощью соотношения (п. 5.2) получим характеристическое уравнение
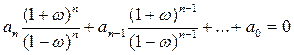 , (п. 5.3)
, (п. 5.3)
корни которого для устойчивой системы будут лежать в левой полуплоскости комплексной w-плоскости.
Это условие относительно переменной w совпадает с условием устойчивости для непрерывных систем управления. Поэтому для определения устойчивости импульсной системы управления по уравнению (п.5.3) можно использовать алгебраические критерии устойчивости, разработанные для непрерывных систем управления.
Рассмотрим подробно методику такого способа определения устойчивости импульсных систем.
Приведя слагаемые к общему знаменателю, уравнение (п. 5.3) можно представить следующим образом
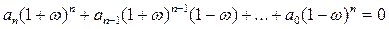 .
.
После раскрытия скобок и приведения подобных членов получается характеристическое уравнение относительно переменной w в каноническом виде
 (п. 5.4)
(п. 5.4)
Для определения устойчивости импульсной системы по этому уравнению в свете вышеизложенного можно применим критерий у Рауса-Гурвица.
Рассмотрим конкретный пример.
Для системы первого порядка (n=1) характеристическое уравнение имеет вид
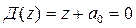 .
.
Или после замены переменных через соотношение (п.5.2) и приведения подобных членов получим, что
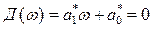 ,
,
где  .
.
Условием устойчивости по критерию Рауса-Гурвица для системы первого и второго является порядков положительность всех коэффициентов характеристического уравнения. Для рассматриваемого случая это
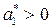 и
и 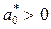 .
.
Или 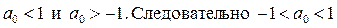 .
.
Из этого следует, что даже при положительных коэффициентах исходного характеристического уравнения первого порядка импульсная система может оказаться не устойчивой. Из физики работы системы это объясняется тем, что период квантования по времени может быть таким большим, что вызванное им запаздывание может сделать замкнутую систему неустойчивой.
|
|
|
Для системы второго порядка
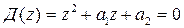 ,
,
после замены переменных через соотношение (п. 5.2.) получим
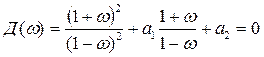 ,
,
или после соответствующих преобразований характеристическое уравнение будет иметь следующий вид
 . (п. 5.5)
. (п. 5.5)
В соответствии с критерием Рауса-Гурвица устойчивость также определятся из положительности коэффициентов уравнения (п. 5.6)
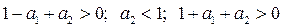 .
.
Для системы третьего порядка, имеющей характеристическое уравнение
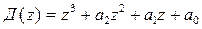 ,
,
также производится замена переменных.
После соответствующих преобразований условия устойчивости определяются из положительности коэффициентов характеристического уравнения Д(w):
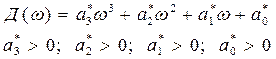
и главного минора определителя Гурвица
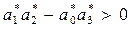 .
.
Связь между коэффициентами  и
и 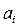 определяется по той же методике, что и для систем первого и второго порядков.
определяется по той же методике, что и для систем первого и второго порядков.
|
|
|


