 |
Задачи на условный экстремум
|
|
|
|
Ранее были рассмотрены случаи вариационных задач, когда в качестве
класса допустимых кривых принималась совокупность кривых, соединяющих
или две заданные точки, или точки заданных линий. Однако существуют
задачи, в которых на допустимые функции накладываются помимо краевых 36
условий некоторые дополнительные – так называемые условия связи.
Подобные задачи принято называть задачами на условный экстремум.
Примером может служить задача Дидоны, где в качестве такого
«дополнительного» условия выступает требование, что длины графиков
допустимых функций имеют заданное значение.
Для решения задач на условный экстремум обычно используется метод
множителей Лагранжа. Это правило было впервые сформулировано им для
исследования вариационных задач с ограничениями, и только потом – для
конечномерных экстремальных задач.
Метод множителей Лагранжа, метод нахождения условного экстремума функции f(x), где  , относительно m ограничений
, относительно m ограничений  , где i меняется от единицы до m.
, где i меняется от единицы до m.
· Составим функцию Лагранжа в виде линейной комбинации функции  и функций
и функций  , взятых с коэффициентами, называемыми множителями Лагранжа —
, взятых с коэффициентами, называемыми множителями Лагранжа —  :
:

где 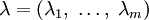 .
.
· Составим систему из  уравнений, приравняв к нулю частные производные функции Лагранжа
уравнений, приравняв к нулю частные производные функции Лагранжа  по
по  и
и  .
.
· Если полученная система имеет решение относительно параметров  и
и  , тогда точка
, тогда точка  может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.
может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.
- Изопериметрические задачи вариационного исчисления и общий метод их решения.
Изопериметрическая задача ставится следующим образом: Даны функционалы J, G1, G2,..., Gn и постоянные l1, l2,..., ln; среди элементов области определения D (J) функционала J, удовлетворяющего уравнениям
|
|
|

требуется найти элемент, доставляющий функционалу J наименьшее значение.
Считается, что область

не пуста.
Частным случаем изопериметрической задачи является задача о наибольшей площади, поставленная в 1.2.2.
Здесь n =1.

За D (J) можно принять множество тех функций из С [ a,b ], которые обращаются в нуль при x=a и x=b (условие 3), а за D (F 1) – множество функций из С (1) [ a,b ], удовлетворяющих тем же условиям (1.3). Очевидно, D (G 1) ⊂ D (J) и пересечение D (G 1) ∩ D (J) не пусто. Будем считать, что функционалы J, G1, G2,..., Gn удовлетворяют требованиям 1, 2, 3. Пересечение линейных многообразий само есть линейное многообразие, поэтому существует элемент  и линейное многообразие M 0 такое, что любой элемент u ∈ D 0 имеет вид u = u + η, η ∈ M 0.
и линейное многообразие M 0 такое, что любой элемент u ∈ D 0 имеет вид u = u + η, η ∈ M 0.
Будем считать, что множество M 0 плотно в рассматриваемом пространстве.
Класс задач вариационного исчисления. Простейшие И. з. (нахождение треугольников и многоугольников заданного периметра, имеющих наибольшую площадь; нахождение замкнутой кривой заданной длины, ограничивающей максимальную площадь; определение замкнутой поверхности заданной площади, ограничивающей наибольший объём, и т. п.) были известны древнегреческим учёным. Общее изучение И. з. началось в 1697, когда Я. Бернулли опубликовал поставленную и частично решенную им И. з.: среди всех кривых данной длины найти кривую, для которой некоторая величина, зависящая от кривой, достигает минимума или максимума. Систематическое исследование И. з. было впервые проведено в 1732 Л. Эйлер ом. Пример И. з.: среди кривых данной длины l, проходящих через точки А и B, найти кривую, для которой площадь криволинейной трапеции (заштрихована на рис.) была бы наибольшей. Площадь криволинейной трапеции равна

длина дуги

Следовательно, задача сводится к нахождению наибольшего значения интеграла (1) при наличии условий (2). Оказывается, что искомая кривая — дуга окружности.
|
|
|

- Решение изопериметрических задач о максимальной площади под кривой заданной длины.
- Задача о геодезических линиях на двумерных плоскостях. Получения общего уравнения для них.
- Задача о положении равновесия абсолютно гибкого, однородного и не растяжимого каната.
- Прямые методы Эйлера и Ритца для приближенного решения вариационных задач.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, т. н. ломаной Эйлера.
Описание:
Пусть дана задача Коши для уравнения первого порядка


где функция  определена на некоторой области
определена на некоторой области  . Решение разыскивается на интервале
. Решение разыскивается на интервале  . На этом интервале введем узлы
. На этом интервале введем узлы

Приближенное решение в узлах  , которое обозначим через
, которое обозначим через  определяется по формуле
определяется по формуле

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
Метод Ритца — прямой метод нахождения приблизительного решения краевых задач вариационного исчисления. Метод назван в честь Вальтера Ритца, который предложил его в 1909 году
Метод предусматривает выбор пробной функции, которая должна минимизировать определенный функционал, в виде суперпозиций известных функций, которые удовлетворяют граничным условиям. Тогда задача сводится к поиску неизвестных коэффициентов суперпозиции. Пространственный оператор в операторном уравнении, который описывает краевую задачу, должен быть линейным, симметрическим и положительно-определенным.
Пусть поставлена задача нахождения точки минимума ограниченного снизу функционала  на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов
на сепарабельном банаховом пространстве U. Задается нек-рая (т. <н. координатная) система элементов 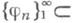
 , полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1 ,..., j n, т. е. коэффициенты
, полная в U. По P.м. минимизирующий элемент в п- мприближении разыскивается в линейной оболочке первых пкоординатных элементов j1 ,..., j n, т. е. коэффициенты  приближения
приближения

определяются из условия минимальности J (и п)среди элементов указанного вида. Вместо координатной системы можно задать последовательность подпространств
|
|
|
 , не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением
, не обязательно вложенных друг в друга. Пусть Н - гильбертово пространство со скалярным произведением  , А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения
, А - самосопряженный, положительно определенный, вообще говоря, неограниченный оператор в H, а Н А - гильбертово пространство, получаемое пополнением области определения  оператора Апо норме
оператора Апо норме  , порожденной скалярным произведением
, порожденной скалярным произведением 
 . Пусть нужно решить задачу
. Пусть нужно решить задачу
 (1)
(1)
Она равносильна задаче отыскания точки минимума квадратичного функционала

к-рый можно записать в виде

где и 0=А -1f- решение уравнения (1). Пусть  , n=1, 2,...,- замкнутые (обычно конечномерные) подпространства такие, что
, n=1, 2,...,- замкнутые (обычно конечномерные) подпространства такие, что  при
при  для каждого
для каждого  , где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и 0 к решению уравнения (1); при этом
, где Р п - ортопроектор в HA, проектирующий на Н п. Минимизируя Ф в Н п, получают ритцовское приближение и n=Р п и 0 к решению уравнения (1); при этом 
при  . Если
. Если  - базис Н n, то коэффициенты элемента
- базис Н n, то коэффициенты элемента
 (2)
(2)
определяются из линейной системы уравнений
 (3)
(3)
К ритцовскому приближению можно прийти и минуя вариационную формулировку задачи (1). А именно, определив приближение (2) из условий

(м е т о д Г а л е р к и н а), приходят к той же системе уравнений (3). Поэтому Р. м. для уравнения (1) иногда наз. м е т о д о м Р и т ц а - Г а л е р к и н а.
Р. м. широко применяется и при решении задач на собственные значения, краевых задач и вообще операторных уравнений. Пусть Аи В - самосопряженные операторы в Н, причем А положительно определен, Вположителен,  и оператор А - 1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А - 1 Всамосопряжен и положителен в HA и спектр задачи
и оператор А - 1 Ввполне непрерывен в пространстве Н A. В силу наложенных условий А - 1 Всамосопряжен и положителен в HA и спектр задачи  (4) состоит из положительных собственных значений:
(4) состоит из положительных собственных значений:
 при
при 
Р. м. основан на вариационной характеризации собственных значений. Напр.,  и, проведя минимизацию лишь по подпространству
и, проведя минимизацию лишь по подпространству  , получают ритцовские приближения
, получают ритцовские приближения  к l1, и 1. Если
к l1, и 1. Если  , как и выше, базис Н п, то ритцовские приближения
, как и выше, базис Н п, то ритцовские приближения  к
к  , определяются из уравнения
, определяются из уравнения

а вектор коэффициентов  приближения
приближения
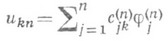
к  определится как нетривиальное решение линейной однородной системы
определится как нетривиальное решение линейной однородной системы  . Р. м. приближает собственные значения сверху, то есть
. Р. м. приближает собственные значения сверху, то есть  , k=l,..., п. Если k-е собственное значение задачи (4) простое
, k=l,..., п. Если k-е собственное значение задачи (4) простое  , то быстрота сходимости Р. м. характеризуется соотношениями
, то быстрота сходимости Р. м. характеризуется соотношениями
|
|
|

где  при
при  . Подобные соотношения распространяются и на случай кратного
. Подобные соотношения распространяются и на случай кратного  , но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.
, но требуют нек-рых уточнений (см. [2]). В. Ритц [4] предложил свой метод в 1908, но ранее Рэлей (Rayleigh) применял этот метод при решении нек-рых задач на собственные значения. В связи с этим Р. м. часто наз. м е т о д о м Р э л е я - Р и т ц а, особенно, если речь идет о решении проблемы собственных значений.
|
|
|


